NoteAI

机器学习 -- 人工智能学习路线（进行中……）

Posted on February 10, 2023 (珠海)
机器学习 

深度学习与炼丹。 经典网络 AlexNet 第一层的卷积内核是 11x11 像素。 为什么是 11 不是 10，不是 12？不知道，作者写论文的时候也没讲。 为什么有 9 层，为什么第二层就变成 5x5，后面又变成 3x3 了？作者也没说。 甚至，为什么这个内核的大小越来越小也没有交代。 深度学习像一剂成分复杂、原理不明的药。 卷积架构 适合图像处理，RNN & Transformer 架构适合处理语言。 实践中，根据经验多试几个，哪个网络效果更好就用那个。

机器学习的学习路径

使用 Kaggle 的目的主要是将技能落在实处，防止练就一身屠龙之技。 机器学习最大的幻觉就是觉得自己什么都懂了，但等到真的使用时发现并不奏效，而 Kaggle 是一个低成本的应用机器学习的机会。

工业界百分之六十的时间都在清理数据，这和学术界干净且规则化的现成数据完全不同。

一定要学习优质资源，而不是不分青红皂白的学习。

获取数据的方式主要有三种：开放数据（以学术界开放为主，如 ImageNet 和 LFW）、第三方数据公司的付费数据和结合自身业务产生的数据。


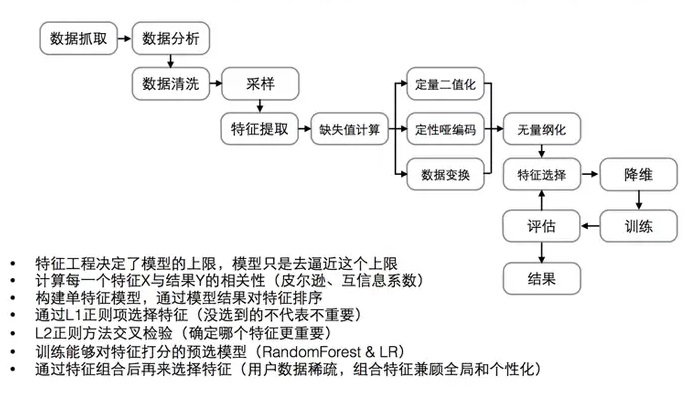
特征工程

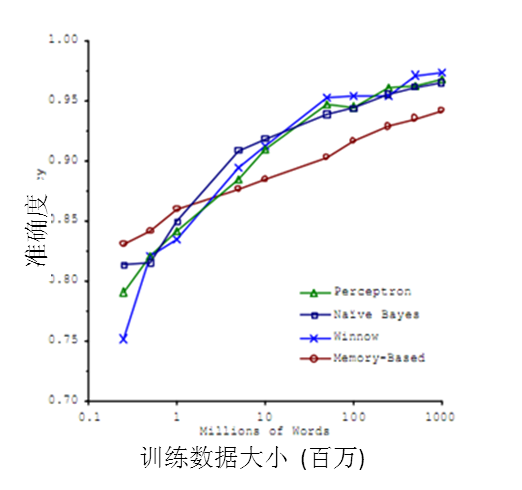
It's not who has the best algorithm that wins. It's who has the most data.

学习地图

微积分：MIT 18.01, MIT 18.02 线性代数：MIT 18.06 概率论与数理统计：MIT 6.041 凸优化：CVX101

建议可以从吴恩达 / 李宏毅的课程入门，看完后可进一步的根据自己的研究方向选择，比如 CV 方向的可以看李飞飞的 CS231n 课程，最后再直接上手 Pytorch 去学习官方示例，把代码跑起来。

深度学习与计算机视觉—斯坦福 CS231n https://liumin.blog.csdn.net/article/details/125546056 通道洗牌、变形卷积核、可分离卷积？盘点卷积神经网络中十大令人拍案叫绝的操作。 https://www.jianshu.com/p/71804c97123d

胡浩基？李航 . 统计学习方法 ?，周志华 . 机器学习 ?

  1. 《统计学习方法》李航？
  2. 《机器学习课》邹博？周志华？西瓜书？
  3. 深度学习 计算机视觉 CV、Paper 阅读等等 …

学习计划：

  1. 从新视频，查漏补缺。
  2. 查看 week 文档。
  3. 做作业。
  4. 最后 2022 版本全部从新过一遍。

第一周的完成了。该第二周了。 第二周 3.1 - 5.7 第三周 6.1 - 7.4 第四周 8.1 - 8.7 第五周 9.1 - 9.8 第六周 10.0 - 11.5 第七周 12.1 - 12.6 第八周 13.1 - 14.7 第九周 15.1 - 16.6 第十周 17.1 - 19.1

Review

  • code\Programming Exercise( 代码作业 ).pdf
  • code\ex2-logistic regression\ex2.pdf
  • code\ex2-logistic regression\ex2data1.txt
  • code\ex2-logistic regression\ex2data2.txt
  • code\ex2-logistic regression\ML-Exercise2.ipynb
  • code\ex3-neural network\ex3.pdf
  • code\ex3-neural network\ex3data1.mat
  • code\ex3-neural network\ex3weights.mat
  • code\ex3-neural network\ML-Exercise3.ipynb
  • code\ex3-neural network\ 向量化标签 .png
  • code\ex4-NN back propagation\ex4.pdf
  • code\ex4-NN back propagation\ex4data1.mat
  • code\ex4-NN back propagation\ex4weights.mat
  • code\ex4-NN back propagation\ML-Exercise4.ipynb
  • code\ex5-bias vs variance\ex5.pdf
  • code\ex5-bias vs variance\ex5data1.mat
  • code\ex5-bias vs variance\ML-Exercise5.ipynb
  • code\ex6-SVM\ex6.pdf
  • code\ex6-SVM\ML-Exercise6.ipynb
  • code\ex6-SVM\data\emailSample1.txt
  • code\ex6-SVM\data\emailSample2.txt
  • code\ex6-SVM\data\ex6data1.mat
  • code\ex6-SVM\data\ex6data2.mat
  • code\ex6-SVM\data\ex6data3.mat
  • code\ex6-SVM\data\spamSample1.txt
  • code\ex6-SVM\data\spamSample2.txt
  • code\ex6-SVM\data\spamTest.mat
  • code\ex6-SVM\data\spamTrain.mat
  • code\ex6-SVM\data\vocab.txt
  • code\ex7-kmeans and PCA\ex7.pdf
  • code\ex7-kmeans and PCA\ML-Exercise7.ipynb
  • code\ex7-kmeans and PCA\data\bird_small.mat
  • code\ex7-kmeans and PCA\data\bird_small.png
  • code\ex7-kmeans and PCA\data\ex7data1.mat
  • code\ex7-kmeans and PCA\data\ex7data2.mat
  • code\ex7-kmeans and PCA\data\ex7faces.mat
  • code\ex8-anomaly detection and recommendation\ex8.pdf
  • code\ex8-anomaly detection and recommendation\ML-Exercise8.ipynb
  • code\ex8-anomaly detection and recommendation\data\ex8_movieParams.mat
  • code\ex8-anomaly detection and recommendation\data\ex8_movies.mat
  • code\ex8-anomaly detection and recommendation\data\ex8data1.mat
  • code\ex8-anomaly detection and recommendation\data\ex8data2.mat
  • code\ex8-anomaly detection and recommendation\data\movie_ids.txt
  • docx\README.md
  • docx\ 机器学习的数学基础.docx
  • markdown\1.CS229-LinearAlgebra.md
  • markdown\2.CS229-Prob.md
  • markdown\math.md
  • markdown\README.md
  • markdown\SUMMARY.md
  • markdown\week1.md
  • markdown\week10.md
  • markdown\week2.md
  • markdown\week3.md
  • markdown\week4.md
  • markdown\week5.md
  • markdown\week6.md
  • markdown\week7.md
  • markdown\week8.md
  • markdown\week9.md
  • ppt\Lecture1.pptx
  • ppt\Lecture10.pptx
  • ppt\Lecture11.pptx
  • ppt\Lecture12.pptx
  • ppt\Lecture13.pptx
  • ppt\Lecture14.pptx
  • ppt\Lecture15.pptx
  • ppt\Lecture16.pptx
  • ppt\Lecture17.pptx
  • ppt\Lecture18.pptx
  • ppt\Lecture2.pptx
  • ppt\Lecture3.pptx
  • ppt\Lecture4.pptx
  • ppt\Lecture5.pptx
  • ppt\Lecture6.pptx
  • ppt\Lecture7.pptx
  • ppt\Lecture8.pptx
  • ppt\Lecture9.pptx

英语

作业 exercise

Python 实现。

第一周

首先，我们将创建一个以参数 θ 为特征函数的代价函数 \(J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{ { {\left( { {h}_{\theta }}\left( { {x}^{(i)}} \right)-{ {y}^{(i)}} \right)}^{2}}}\)

其中： \({ {h}_{\theta }}\left( x \right)={ {\theta }^{T}}X={ {\theta }_{0}}{ {x}_{0}}+{ {\theta }_{1}}{ {x}_{1}}+{ {\theta }_{2}}{ {x}_{2}}+...+{ {\theta }_{n}}{ {x}_{n}}\)

# 计算代价函数函数。
def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

# 批量梯度下降
# alpha -- 学习速率
# iters -- 要执行的迭代次数
def gradientDescent(X, y, theta, alpha = 0.01, iters = 1000):
    temp = np.matrix(np.zeros(theta.shape)) # 跟 theta 一样的矩阵
    parameters = int(theta.ravel().shape[1]) # theta 个数，ravel() 将数组维度拉成一维数组
    cost = np.zeros(iters) # 初始化 cost 数组。

    for i in range(iters):
        error = (X * theta.T) - y

        for j in range(parameters):
            term = np.multiply(error, X[:,j])
            temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))

        theta = temp
        cost[i] = computeCost(X, y, theta)

    return theta, cost

# 多变量线性回归
# 预处理步骤 - 特征归一化
def orgfunc(data2):
    data2 = (data2 - data2.mean()) / data2.std()
    data2.head()

# scikit-learn 的线性回归算法
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y)

# 正规方程
def normalEqn(X, y):
    theta = np.linalg.inv(X.T@X)@X.T@y # X.T@X 等价于 X.T.dot(X)
    return theta

参考资料快照
参考资料快照
本文短链接：
If you have any questions or feedback, please reach out .
自由转载-非商用-非衍生-保持署名
（创意共享 3.0 许可证）