机器学习 -- Attention is all you need
注意力机制。网上很多文章,但是我这篇文章应该是最浅显易懂的。零基础都能看懂,并且学会手算。 各位大牛帮忙 Review,如果存在错误或者不严谨的地方,我再改改。
从基本原理来看,目前的大语言模型没有跳出概率统计这个框架。 大模型可被视为是由已有语料压缩而成的知识库,生成结果的语义正确性高度依赖于数据的空间广度、时间深度以及分布密度,更高度依赖于数据的质量。 模型本身无法产生新的东西,其生成的内容取决于对大量文本内容的统计,如果某些内容反复出现,它们大概率就会将之视为“合理存在”的内容。
简单描述
注意力机制通俗解释 以淘宝搜索为例:
-
查询 :我们输入查询(query,$Q$),比如“笔记本”。
-
计算相似性 :淘宝后台拿到这个查询 Q,并用这个查询 Q 和后台商品的关键字(key,$K$)进行相似度计算, 得到物品和我的查询的相似性(或者说物品对应的相似性权重),相似度越高,越有可能推送给我们。
-
得到价值 :这个时候还有考虑物品的价值(value,$V$),这个 V 不是指物品值几块钱, 而是物品在算法中的价值。如果商家给了淘宝广告费,或物品物美价廉、评价好、点赞多等等,那么就越有可能推送给我们。
-
计算带权重的价值 :用相似性乘价值,就得到了带权重的价值。 淘宝最后会按照值从高到低的顺序返回显示在页面上。
向量描述
\[\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V\]上面的整个过程用向量矩阵表达,就是 注意力机制。 往往得到的矩阵非常庞大。 高维空间的 Token 表示,往往蕴含很多相关信息。
注意力机制的本质是一种权重分配机制,即对不同重要程度的信息赋予不同的权重,让系统学会注意力关注重点信息,同时忽略无关信息。
自注意力是对每个输入赋予的权重取决于输入数据之间的关系,即通过输入项内部之间的相互博弈决定每个输入项的权重。
class ScaledDotProductAttention(nn.Module):
def __init__(self, temperature, attn_dropout=0.1):
super().__init__()
self.temperature = temperature
self.dropout = nn.Dropout(attn_dropout)
def forward(self, q, k, v, mask=None):
attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
if mask is not None:
attn = attn.masked_fill(mask == 0, -1e9)
attn = self.dropout(F.softmax(attn, dim=-1))
output = torch.matmul(attn, v)
return output, attn
手算示例
$Q$、$K$、$V$ 都是 $X$ 的线性变换。 为了方便,我们直接用 $X$ 做自注意力机制。
\[\text { Attention }(X, X, X)=\operatorname{softmax}\left(\frac{X X^T}{\sqrt{d_k}}\right) X\]假如 $X$ “笔记本”每个字的向量表示分别是:
- “笔”
[1, 2, 1, 2, 1] - “记”
[1, 1, 1, 2, 1] - “本”
[3, 2, 1, 1, 1]
$X^T$ 就是:
| “笔” | ”记” | “本” |
|---|---|---|
| 1 | 1 | 3 |
| 2 | 1 | 2 |
| 1 | 1 | 1 |
| 2 | 2 | 1 |
| 1 | 1 | 1 |
那么 $XX^T$ 就是:
| ~ | “笔” | ”记” | “本” |
|---|---|---|---|
| “笔“ | 11 | 9 | 11 |
| “记” | 9 | 8 | 9 |
| “本” | 11 | 9 | 16 |
而分母 $\sqrt{d_k}$ 可以先不管,是个常数,这个的目的是保证梯度的。 “$\sqrt{d_k}$,影响 $softmax$ 分布,没有它某个 Token 容易出现极端概率。”

While for small values of $d_k$ the two mechanisms perform similarly, additive attention outperforms dot product attention without scaling for larger values of $d_k$. We suspect that for large values of $d_k$, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients. To counteract this effect, we scale the dot products by $\frac{1}{\sqrt{d_k}}$.
$\operatorname{softmax}({X X^T})$ 就是:
| ~ | “笔” | ”记” | “本” |
|---|---|---|---|
| “笔“ | 0.468 | 0.064 | 0.468 |
| “记” | 0.422 | 0.156 | 0.422 |
| “本” | 0.0069 | 9.05E-04 | 0.992 |
这里 每行的和都是 等于 $1$ 的,这个是 $softmax$ 函数的特性。
最终 $\operatorname{softmax}\left(X X^T\right) X$ 就成了:
- “笔”
[1.94, 1.94, 1, 1.53, 1] - “记”
[1.84, 1.84, 1, 1.58, 1] - “本”
[2.98, 2, 1, 1.01, 1]
此时每个汉字在高维空间的位置 就被更新了。 是不是很神奇?!
感觉注意力机制是一种可学习的高级核函数的支持向量机。 GPT 这样的语言模型,表面上是在学习预测下一个词(next token prediction)。实质上,它在匹配语言的分布,学习语言的隐含规律。比如,在「我爱吃苹果」这句话里,「我爱吃」后面更可能出现「苹果」,而不是「砖头」,这反映了语言的内在知识。
深度解析
本质上 Transformer 还是神经网络,反向传播照常进行! 能「让每个 token 关注其他所有 token」
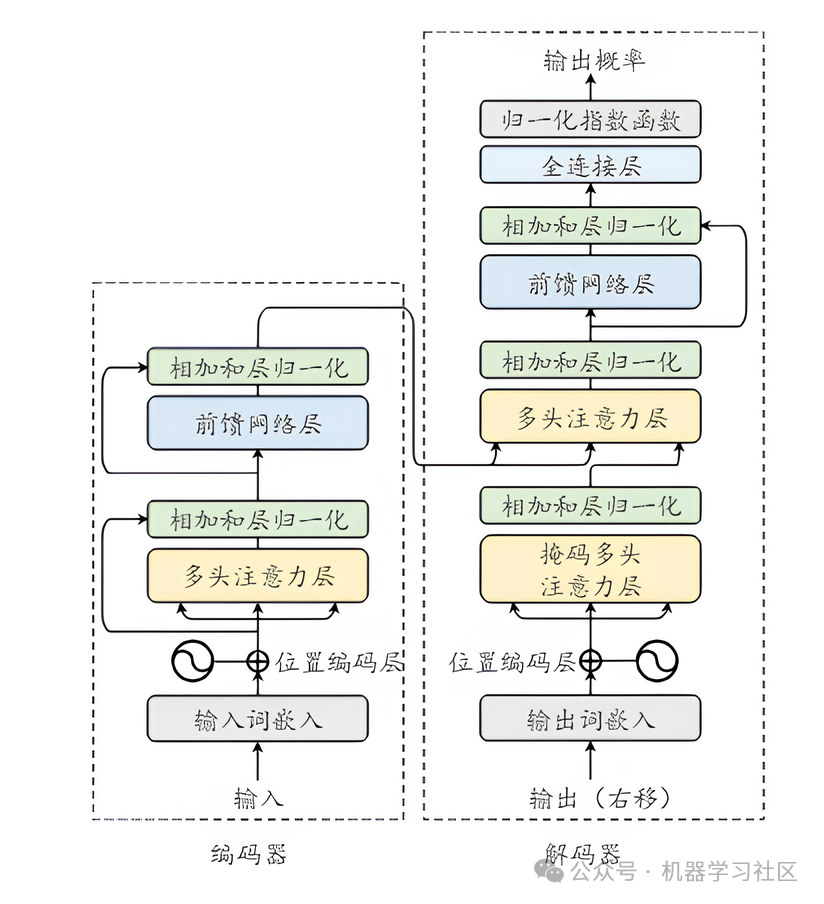
我们拆开来看,Transformer 是一个堆叠结构,最基本的组件是:
Input → Embedding → Multi-Head Attention → FFN → Output
其中,所有的 Linear 层都是含参数的!比如:
- q_linear = nn.Linear(hidden_size, hidden_size)
- k_linear = nn.Linear(hidden_size, hidden_size)
- v_linear = nn.Linear(hidden_size, hidden_size)
- o_linear = nn.Linear(hidden_size, hidden_size)
- FFN 内的两个全连接层也是 Linear
这些层都拥有各自的 W 和 b,通过梯度反向传播自动更新。
那注意力里的 softmax 和点积怎么办?
很多人以为 Attention 只是计算了一堆系数,不能反向传播。其实完全可以! 比如这一行:
attention_scores = torch.matmul(query, key.transpose(-1, -2)) / sqrt(d_k)
这是一堆矩阵乘法 + 除法 + softmax + 加权求和操作,它们都支持梯度传播,在 PyTorch 中每一步都是可导的。
只要在训练时写的是:
loss = criterion(outputs, labels)
loss.backward()
那么:
- q_linear、k_linear、v_linear、o_linear 的参数都会被更新;
- FFN 的全连接层也会被更新;
- 整个 Attention 路径是可导的链式结构,没有断点。
换个角度理解:Attention 只是一个「带分数的加权平均」
我们用人话描述一下 Attention: 就是拿 Q 去和每个 K 做个点积,比比“谁更相关”,然后把 V 加权平均一下,得到一个新的向量。
Q、K、V 都是从原始输入通过可训练的 Linear 层映射出来的,这些线性变换就带有权重参数 W 和偏置 b。
这整个流程,就是一个很复杂的「函数」,它也完全可以被反向传播优化。
Transformer 的训练跟 CNN 没本质区别
- CNN 是卷积核滑动提取特征;
- RNN 是时间步递归传播状态;
- Transformer 是 Attention 模块进行全局信息整合。
它们都是神经网络,只不过「信息整合」的方式不同,但 都是端到端优化、都靠 loss.backward() 完成权重调整。
「Transformer 的反向传播呢?如何调整权重参数?」 简单说就是:
- 权重来自所有的 Linear 层(Q、K、V、O、FFN)
- 训练过程使用的是标准的反向传播机制
- 每一步的算子(矩阵乘、softmax、加法)都支持链式求导
- 你看到的 Attention 模块,不是黑盒,而是完整参与优化的计算图的一部分
我们之所以会感觉 Transformer 像「一个黑盒」,很可能是:
- 没看到「代码级别」的 forward + backward;
- 没意识到 softmax/ 点积这些操作也支持求导;
- 被太多只讲公式的文章绕晕了。
建议动手实现一个简化版的 Multi-Head Attention,比如我们训练营里常讲的这个版本:
query = self.q_linear(hidden_state)
key = self.k_linear(hidden_state)
value = self.v_linear(hidden_state)
...
attention_scores = torch.matmul(query, key.transpose(-1, -2)) / sqrt(d_k)
attention_probs = F.softmax(attention_scores, dim=-1)
output = torch.matmul(attention_probs, value)
这段代码每个 Linear 都有参数,都能梯度更新,亲测跑通后你就真理解了。
总结一句话: Transformer 本质上还是一个「全连接 + softmax + 加权平均」的神经网络,每个参数都在被优化,每一层都在被反向传播训练。只有矩阵计算。
更多 …
Attention is all you need transformer bert @vcubingx
What does it mean for computers to understand language? | LM1
https://www.youtube.com/watch?v=1il-s4mgNdI https://www.bilibili.com/video/BV1jx4y1t7Lq/
Why Recurrent Neural Networks are cursed | LM2
https://www.youtube.com/watch?v=rTz6hadM1Lg https://www.bilibili.com/video/BV1qi421e7DH/
How did the Attention Mechanism start an AI frenzy? | LM3
注意力机制被用于 Transformer 中,起源于修复 RNN 的问题。 https://www.youtube.com/watch?v=lOrTlKrdmkQ https://www.bilibili.com/video/BV1Dw4m1e74b/
Transformer 论文逐段精读【论文精读】
https://www.bilibili.com/video/BV1pu411o7BE/ 假设更一般,对数据信息的抓取能力更差,所以需要更多数据更大的模型才能训练出来。
大型语言模型中的注意力机制图解
https://www.bilibili.com/video/BV1ki4y1871e/ 这段文字是关于注意力机制的讲解,作者是塞拉诺学院的路易斯 · 塞拉诺。视频主要介绍了注意力机制在大型语言模型中的作用,以及如何使用注意力来解决词义歧义问题。作者首先解释了嵌入的概念,然后详细介绍了自我注意力和多头注意力的原理和应用。
参考资料快照
- https://github.com/jadore801120/attention-is-all-you-need-pytorch/blob/master/transformer/Modules.py
- https://www.youtube.com/watch?v=1il-s4mgNdI
- https://www.bilibili.com/video/BV1jx4y1t7Lq/
- https://www.youtube.com/watch?v=rTz6hadM1Lg
- https://www.bilibili.com/video/BV1qi421e7DH/
- https://www.youtube.com/watch?v=lOrTlKrdmkQ
- https://www.bilibili.com/video/BV1Dw4m1e74b/
- https://www.bilibili.com/video/BV1pu411o7BE/
- https://www.bilibili.com/video/BV1ki4y1871e/
- 机器学习 -- 大型语言模型简史:从 Transformers (2017) 到 DeepSeek-R1(2025) | 20 Feb 2025
- 机器学习 -- DALL·E 2 & 扩散模型 | 21 Dec 2024
- 机器学习 -- 学术论文解读系列(进行中) | 04 Oct 2024
- 机器学习 -- 经典论文 ViT (Vision Transformer) | 24 Jul 2024
- 机器学习 -- 跟李沐学 AI【论文精读】(进行中) | 09 Jul 2024
- 机器学习 -- Attention is all you need | 30 Jun 2024
- 机器学习笔记 -- 3Blue1Brown 深度学习 Deep Learning(已完成) | 29 Jun 2024
- 机器学习 -- 李宏毅 2021/2022 春机器学习课程(进行中) | 31 Aug 2023
- 机器学习 -- 实用机器学习 李沐(进行中) | 31 Aug 2023
- 机器学习 -- ChatGPT Prompt 提示词 吴恩达(进行中) | 28 Jul 2023
- 机器学习 -- 浙江大学 · 机器学习(已完成) | 12 Feb 2023
- 机器学习 -- 人工智能学习路线(进行中……) | 10 Feb 2023
- 机器学习 -- 北交 / 图像处理与机器学习(已完成) | 03 Dec 2022
- 机器学习笔记 -- 人工智能 机器学习 算法概览(已完成) | 13 Oct 2022
- 机器学习笔记 -- 神经网络内部发生了什么?深度学习可视化 | 13 Oct 2022
- 机器学习 -- 吴恩达机器学习 Review(已完成) | 31 Aug 2022
- 机器学习 -- 吴恩达深度学习(进行中) | 31 Aug 2022
- 机器学习 -- 吴恩达机器学习(已完成) | 31 Aug 2022
- 机器学习笔记 -- 神经网络和深度学习简史 | 26 Dec 2020
 .
.