机器学习 -- 吴恩达机器学习(已完成)
入门的话,本科的数学分析,线性代数,概率论与数理统计足够了。 微积分:MIT 18.01, MIT 18.02 线性代数:MIT 18.06 概率论与数理统计:MIT 6.041 凸优化:CVX101
人工智能依然不会思考,但依靠亿万次运算也足够在很多工作上处理地比大多数人更好。人们讨论的新问题是,人工智能会不会强化偏见。
吴恩达

已经完成
- 吴恩达机器学习系列课程
- https://www.coursera.org/specializations/deep-learning
-
https://www.coursera.org/learn/machine-learning-course/home/week/1
黄海广– 已经完成。
-
图像处理 & 机器学习– 已经完成。
- https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
- http://www.ai-start.com/ml2014/
- https://scruel.github.io/Notes-ML-AndrewNg/
有监督学习和无监督学习
监督(supervised)= 标签(label),是否有监督,就是输入数据(input)是否有标签,有标签则为有监督学习,没标签则为无监督学习。 至于半监督学习,就是一半(一点点)数据有标签,一半(极其巨大)数据没标签。
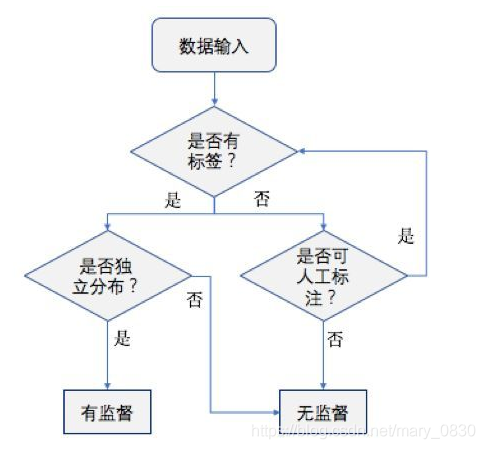
监督学习
定义:根据已有的数据集,知道输入和输出结果之间的关系。根据这种已知的关系,训练得到一个最优的模型。 也就是说,在监督学习中训练数据既有特征(feature)又有标签(label),通过训练,让机器可以自己找到特征和标签之间的联系, 在面对只有特征没有标签的数据时,可以判断出标签。
监督学习的分类:回归(Regression)、分类(Classification)。
无监督学习
定义:我们不知道数据集中数据、特征之间的关系,而是要根据聚类或一定的模型得到数据之间的关系。
Cocktail party problem algorithm: \([W, s, v]=\operatorname{svd}\left((\operatorname{repmat}(\operatorname{sum}(x . * x, 1), \operatorname{size}(x, 1), 1) . * x) * x^{\prime}\right)\)
note ** xx are the mixed microphone measurements (one per column) ** W is the unmixing matrix.
% W = kica(xx);
yy = sqrtm(inv(cov(xx')))*(xx-repmat(mean(xx,2),1,size(xx,2)));
[W,ss,vv] = svd((repmat(sum(yy.*yy,1),size(yy,1),1).*yy)*yy');
Octave P6 start…
1-1. 欢迎参加《机器学习》课程 06:56
完成了。
1-2. 什么是机器学习? 07:15
完成了。
1-3. 监督学习 12:30
定义:根据已有的数据集,知道输入和输出结果之间的关系。
1-4. 无监督学习 14:14
定义:我们不知道数据集中数据、特征之间的关系,而是要根据聚类或一定的模型得到数据之间的关系。
2-1. 模型描述 08:11
yes.
2-2. 代价函数 08:13
代价函数: \(J \left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2}\)

为什么要除以 2,感觉是求导数的时候,刚好能和平方的 2 约掉,整个正向 / 反向传播,数据都是稳定的。
2-3. 代价函数(一) 11:10
完成。
2-4. 代价函数(二) 08:49
等高线图。
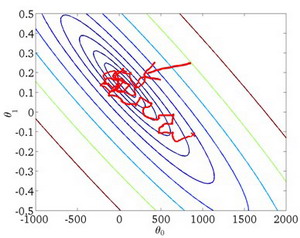
2-5. 梯度下降 11:31
Gradient descent algorithm
repeat until convergence { $\theta_j:=\theta_j-\alpha \frac{\partial}{\partial \theta_i} J\left(\theta_0, \theta_1\right)$ $($ for $j=0$ and $j=1$ $)$ }
- $\alpha$ learning rate ,梯度下降时,我们迈出多大的步子。
- $\frac{\partial}{\partial \theta_i} J\left(\theta_0, \theta_1\right)$ 偏导。
Correct: Simultaneous update \(\begin{aligned} &\text { temp } 0:=\theta_0-\alpha \frac{\partial}{\partial \theta_0} J\left(\theta_0, \theta_1\right) \\ &\text { temp } 1:=\theta_1-\alpha \frac{\partial}{\partial \theta_1} J\left(\theta_0, \theta_1\right) \\ &\theta_0:=\text { temp0 } \\ &\theta_1:=\text { temp1 } \end{aligned}\)
2-6. 梯度下降知识点总结 11:52
完成。鞍点?
2-7. 线性回归的梯度下降 10:21
求偏导后,得到下面两个式子:
\[\begin{aligned} \theta_0 &:=\theta_0-\alpha \frac{1}{m} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right) \\ \theta_1 &:=\theta_1-\alpha \frac{1}{m} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right) \cdot x^{(i)} \end{aligned}\]2-8??
3-1. 矩阵和向量 08:46
矩阵维度:$rows \times cols$
Vector: An nx1 matrix.
3-2. 加法和标量乘法 06:55
3-3. 矩阵向量乘法 13:40
3-4. 矩阵乘法 11:10
ok. 03"13
3-5. 矩阵乘法特征 09:03
- Associative and distributive
- $(AB)C=A(BC)$
- $A(B+C) = AB + AC$
- $(A+B)C = AC + BC$
- 有交换律,没有交换律。
- $(A B)^{T}=B^{T} A^{T}$
3-6. 逆和转置 11:14
并不是每个矩阵都存在逆矩阵。
4-1. 多功能 08:23
4-2. 多元梯度下降法 05:05
Hypothesis: $\quad h_\theta(x)=\theta^T x=\theta_0 x_0+\theta_1 x_1+\theta_2 x_2+\cdots+\theta_n x_n$
Parameters: $\theta_0, \theta_1, \ldots, \theta_n$
Cost function: \(J\left(\theta_0, \theta_1, \ldots, \theta_n\right)=\frac{1}{2 m} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2\)
4-3. 多元梯度下降法演练 I – 特征缩放 08:53
先把每个输入的特征归一化到特定的范围。 可以加快迭代收敛速度。
最简单的方法是令:${ {x}{n}}=\frac{ { {x}{n}}-{ {\mu}{n}}}{ { {s}{n}}}$,其中 ${\mu_{n}}$ 是平均值,${s_{n}}$ 是标准差。

4-4. 多元梯度下降法 II – 学习率 08:59
通常可以考虑尝试些学习率:
$\alpha=0.01,0.03,0.1,0.3,1,3,10$
4-5. 特征和多项式回归 07:40
尝试二次函数拟合。
4-6. 正规方程(区别于迭代方法的直接解法) 16:19
通过解偏导函数等于 0 的情况,直接求出最小值的 $\theta$。
\[\theta=(X^TX)^{-1}X^Ty\]矩阵求逆只能采用高斯消元法,时间复杂度 $O(n^3)$。
4-7. 正规方程在矩阵不可逆情况下的解决方法 06:00
$X^T*X$ 出现不可逆的情况原因可能是:
- 方阵中的两个维度之间存在线性变换关系,导致方阵不满秩(奇异或退化矩阵)
- n(特征数量)相较于 m(样本数量)过大,导致其产生的齐次方程组 $Ax=0$ 不只有零解
4-8. 导师的编程小技巧 03:34
完成了。Octave
5-1. 基本操作 14:00
5-2. 移动数据 16:08
5-3. 计算数据 13:16
伪逆矩阵 $pinv(A)$
5-4. 数据绘制 09:39
plot(t,y);
hold on;
plot(t,y2,'r');
A = magic(5)
imagesc(A)
imagesc(A), colorbar, colormap gray;
5-5. 控制语句:for,while,if 语句 12:57
定义函数:
function [y1,y2] = squareAndCubeThisNumber(x)
y1 = x ^ 2;
y2 = x ^ 3;
function J = costFunctionJ(x, y, theta)
m = size(X, 1);
predictions = X * theta;
sqrErrors = (predictions - y) .^ 2;
J = 1/(2*m) * sum(sqrErrors);
5-6. 矢量 13:49
$h_\theta (x)=\theta^Tx$
\[\theta=\left[\begin{array}{l} \theta_0 \\ \theta_1 \\ \theta_2 \end{array}\right] \quad x=\left[\begin{array}{l} x_0 \\ x_1 \\ x_2 \end{array}\right]\]6-1. 分类 08:09
logistic
6-2. 假设陈述 07:25
Sigmoid function & Logistic function
- $h_{\theta}(x)=g(\theta^Tx)$
- $g(z)=1/(1+e^{-z})$
$h_{\theta}(x) =P(y=1|x;\theta)$
\[\begin{array}{l}P(y=0 \mid x ; \theta)+P(y=1 \mid x ; \theta)=1 \\h_{\theta}(x)=P(y=1 \mid x ; \theta)=1-P(y=0 \mid x ; \theta)\end{array}\]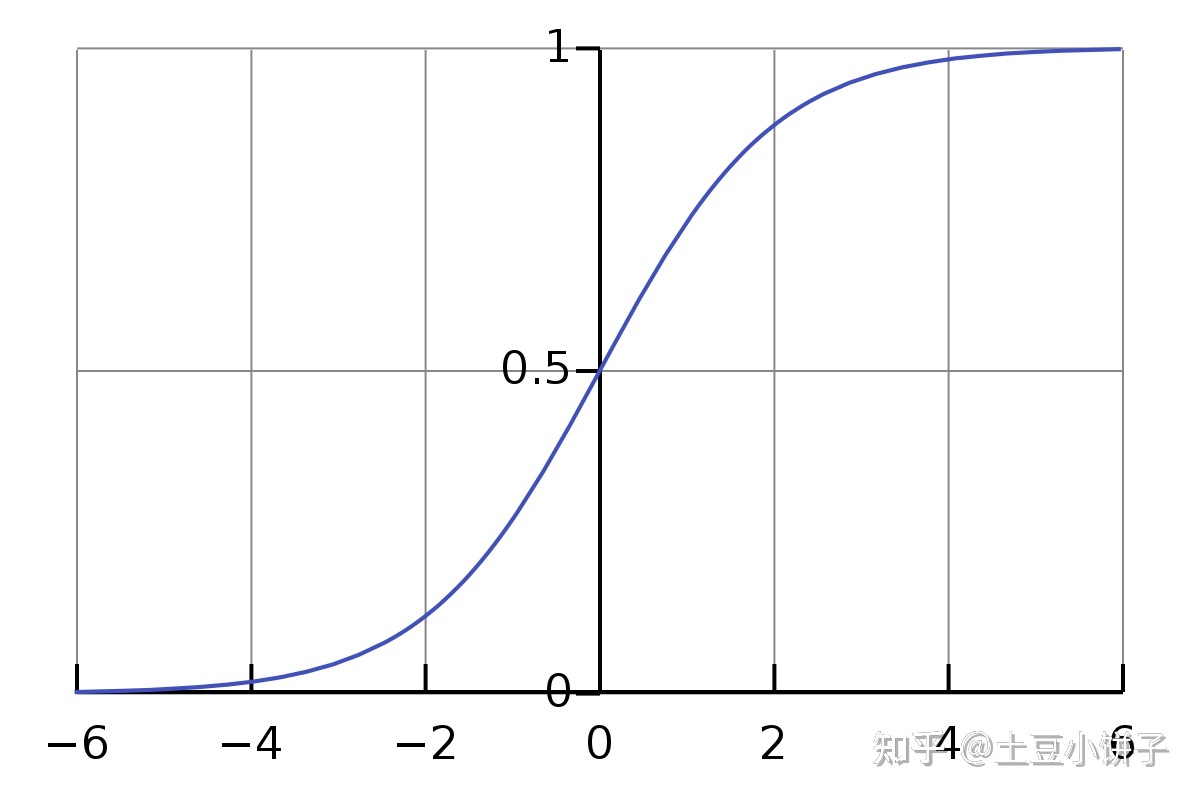
logistic function (S-shape)
Sigmoid 函数求导
基础知识:
- 若 $f\left( x \right)=\frac{1}{x}$,则 $f'\left( x \right)=-\frac{1}{x^{2}}$
- 若 $g\left( x \right)=e^{x}$,则 $g'\left( x \right)=e^{x}$
Sigmoid 函数: $S\left( x \right)=Sigmoid\left( x \right)=\frac{1}{1+e^{-x}}$
求导过程: \(S'\left( x \right)=-\frac{1}{(1+e^{-x})^2}\times(1+e^{-x})'=-\frac{1}{(1+e^{-x})^2}\times(-e^{-x})=\frac{1}{1+e^{-x}}\times\frac{e^{-x}}{1+e^{-x}}=\frac{1}{1+e^{-x}}\times\frac{1+e^{-x}-1}{1+e^{-x}}=S\left( x \right)(1-S\left( x \right))\)
故 Sigmoid 函数的求导结果为: \(S'\left( x \right)=S\left( x \right)(1-S\left( x \right))\)
Sigmoid 函数导数最大值为 0.25,因链式法则需要连乘,故进行反向传播时容易导致梯度消失。前边神经元的权重可能得不到更改。
6-3. 决策界限 14:50
决策边界
6-4. 代价函数 10:25
6-5. 简化代价函数与梯度下降 10:16
统计学中极大似然法得来的,快速寻找参数的方法。

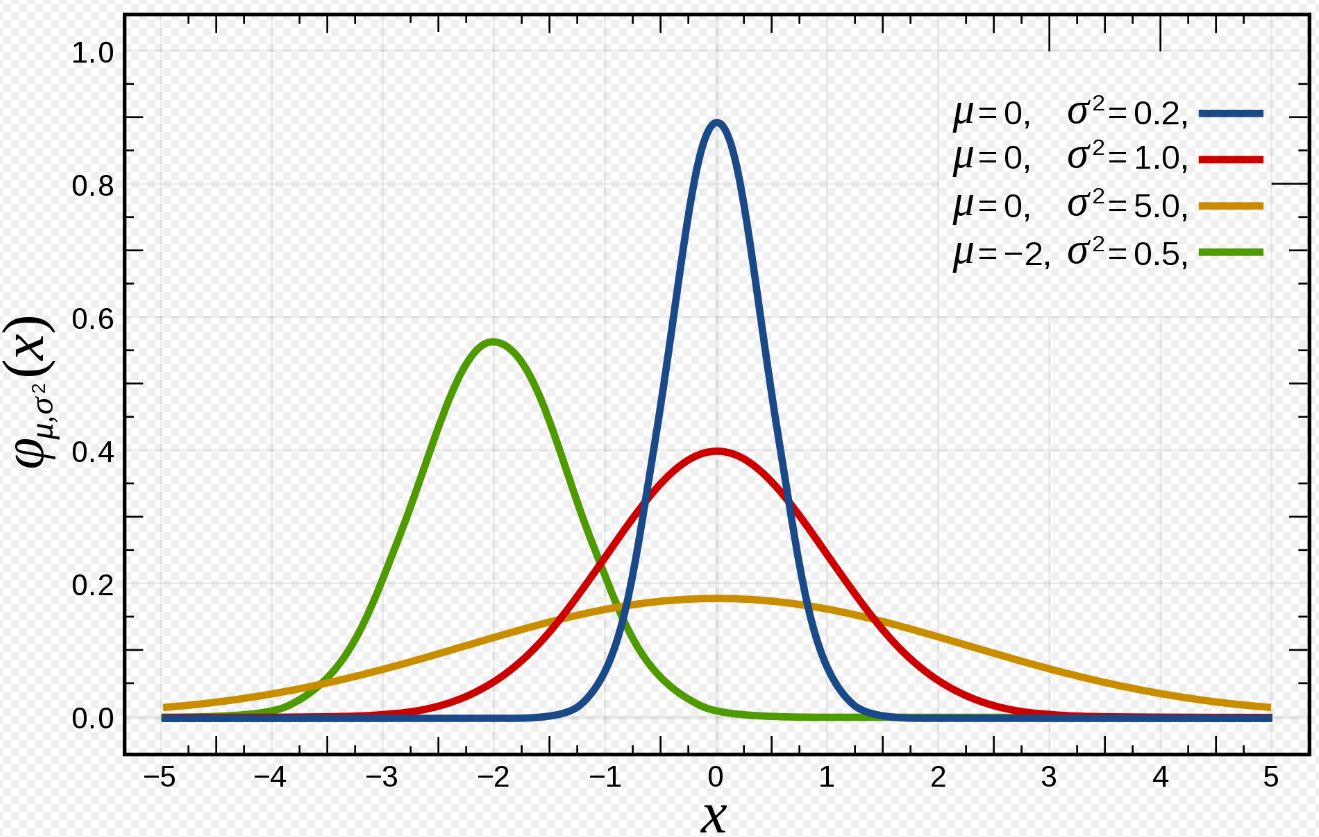
不同参数下高斯分布的形状
6-6. 高级优化 14:07
- Gradient descent
- Conjugate gradient
- BFGS 共轭梯度法
- L-BFGS
Example: \(\begin{aligned} &\theta=\left[\begin{array}{l} \theta_1 \\ \theta_2 \end{array}\right] \\ &J(\theta)=\left(\theta_1-5\right)^2+\left(\theta_2-5\right)^2 \\ &\frac{\partial}{\partial \theta_1} J(\theta)=2\left(\theta_1-5\right) \\ &\frac{\partial}{\partial \theta_2} J(\theta)=2\left(\theta_2-5\right) \end{aligned}\)
6-7. 多元分类:一对多 06:16
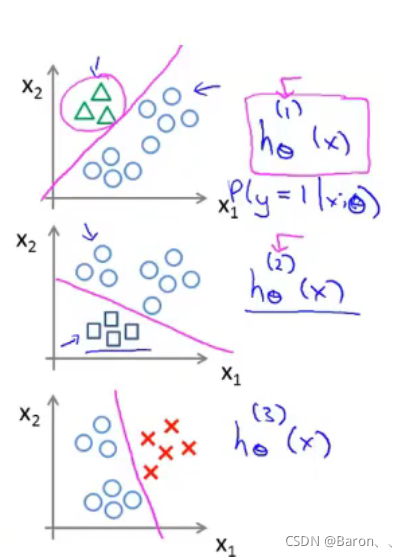
7-1. 过拟合问题 09:43
- undefit, high bias. 高偏差。
- just right.
- overfit, high variance.
过拟合问题(overfitting)
- Underfitting(欠拟合)–> high bias(高偏差)
- Overfitting(过拟合)–> high variance(高方差)
Overfitting: If we have too many features, the learned hypothesis(假设) may fit the training set very well, but fail to generalize to new examples (predict prices on new examples). 模型泛化能力差
addressing overfitting 解决过拟合的方法: options:
- reduce number of features(减少特征数量)
- Manually select which features to keep 人为的保留一些重要的特征值
- Model selection algorithm(模型选择算法)用特征选择算法进行特征的选择(PCA、层次分析法)
- regularization(正则化)
- keep all the features but reduce magnitude/values(但减少参数的大小 / 值)of parameters $\theta_j$.
- 通过对目标函数添加一个参数范数惩罚,限制模型的学习能力。(保留所有的特征,但是减少参数 $\theta$ 的大小)
- Works well when we have a lot of features, each of which contributes a bit to predicting $y$.
- 最终要找到一个平衡点,使得模型能够更好地拟合训练集并且同时具有良好的泛化能力。
- keep all the features but reduce magnitude/values(但减少参数的大小 / 值)of parameters $\theta_j$.
7-2. 代价函数 10:12
\[J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2+\lambda \sum_{j=1}^n \theta_j^2\right]\]7-3. 线性回归的正则化 10:41
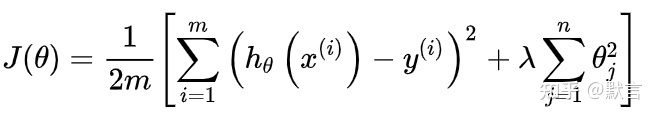
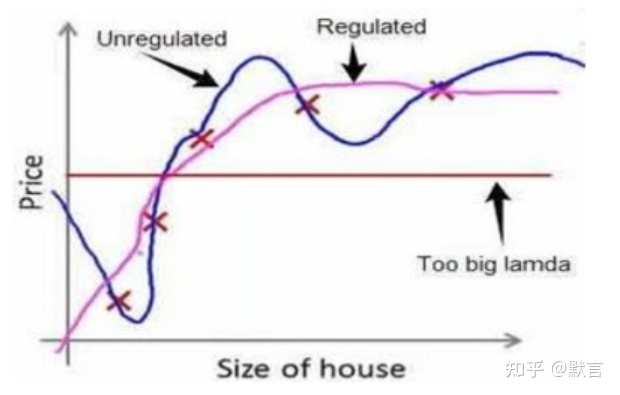
L1 和 L2 正则项
- 当正则化项为 $\lambda\sum_{j=1}^{n}{\theta_{j}^{2}}$ 时,称为 L2 正则化,也称为岭回归(Ridge 回归)。
- 可以防止过拟合。
- 当正则化项为 $\lambda\sum_{j=1}^{n}|{\theta_{j}}|$ 时,称为 L1 正则化,也称为 Lasso 回归。
- 可以产生稀疏模型。
相比 L2 正则化,L 正则化会产生更稀疏的解,此处稀疏性指的是最优值中的一些参数为 0,和 L2 正则化相比,L1 正则化的稀疏性具有本质的不同。
由 L1 正则化导出的稀疏性质已被广泛地用于特征选择机制,特征选择从可用的特征子集选择出有意义的特征,化简问题。 如 Lasso 回归中,L1 惩罚使得部分参数为 0,表明相应的特征可以被安全得忽略。
L1 和 L2 正则先验分别服从什么分布,L1 是拉普拉斯分布,L2 是高斯分布。
7-4. Logistic 回归的正则化 08:35
yes。
8-1. 非线性假设 09:37
8-2. 神经元与大脑 07:48
8-3. 模型展示 Ⅰ 12:02
8-4. 模型展示 Ⅱ 11:47
前向传播。
8-5. 例子与直觉理解 Ⅰ 07:16
AND / OR
8-6. 例子与直觉理解 Ⅱ 10:21
手写数字识别。
8-7. 多元分类 03:52
9-1. 代价函数 06:44
Cost function, Logistic regression: \(J(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2}\)
Neural network: \(\begin{array}{l} h_{\Theta}(x) \in \mathbb{R}^{K} \quad\left(h_{\Theta}(x)\right)_{i}=i^{t h} \text { output }\\ J(\Theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{k=1}^{K} y_{k}^{(i)} \log \left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}+\left(1-y_{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}\right)\right]\\+\frac{\lambda}{2 m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_{l}} \sum_{j=1}^{s_{l+1}}\left(\Theta_{j i}^{(l)}\right)^{2}\end{array}\)
9-2. 反向传播算法 12:00
为了计算代价函数的偏导数 $\frac{\partial}{\partial\Theta^{(l)}_{ij}}J\left(\Theta\right)$, 我们需要采用一种反向传播算法 ,也就是首先计算最后一层的误差,然后再一层一层反向求出各层的误差, 直到倒数第二层。
9-3. 理解反向传播 12:45
有监督学习,机器学习的本质就是数据拟合。 需要理解。你如果不理解,就只是一个调包侠,只有理解了,你才可能成长为一个 AI 算法工程师。 就比如以最简单的,神经网络正向和反向传播为例,你如果不理解整个传播过程,计算过程,就很难继续踏实的学习下去。 比如你如果不理解反向传播,你再往下学,就会感觉稀里糊涂的。
以下通过手动计算过程,模拟神经网络正向 / 反向传播过程,来理解,神经网络参数的更新过程。
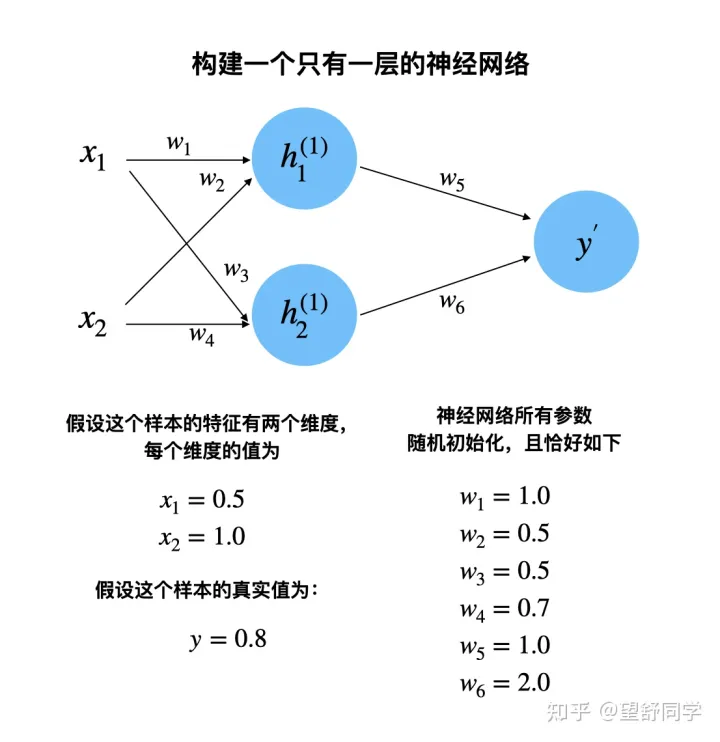
构建一个只有一层的神经网络
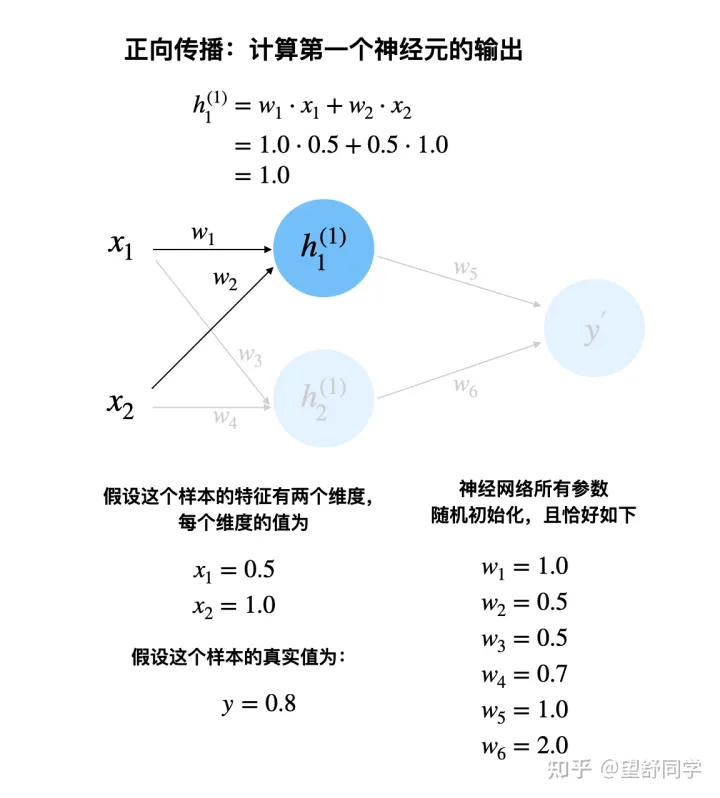
正向传播:计算第一个神经元的输出
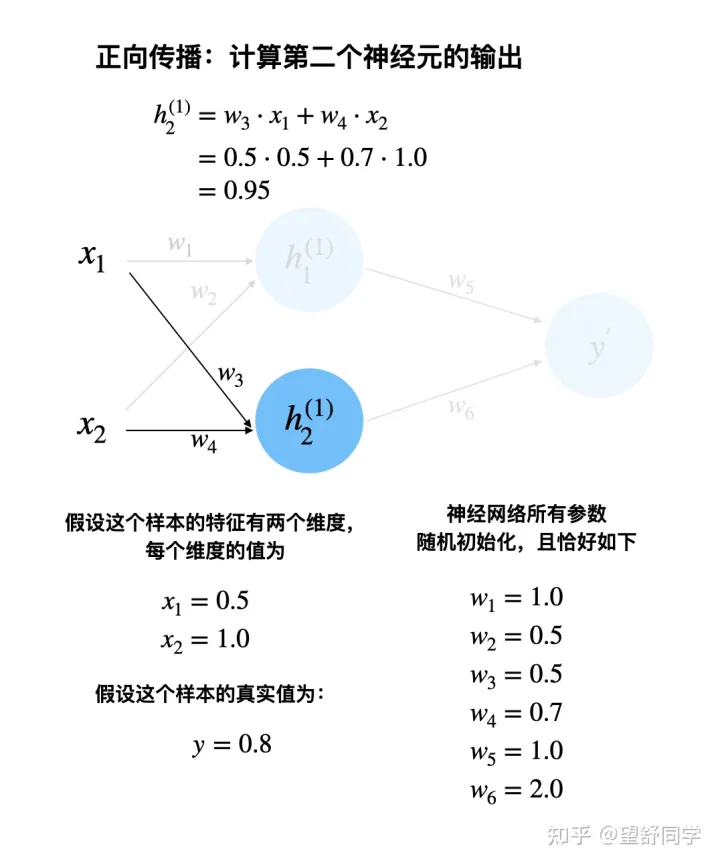
正向传播:计算第二个神经元的输出
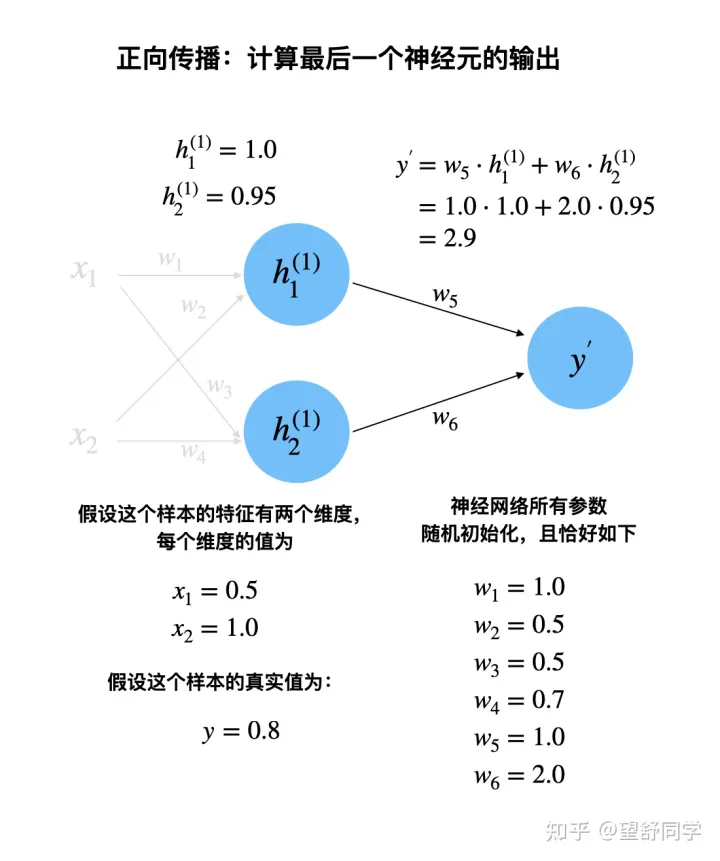
正向传播:计算最后一个神经元的输出
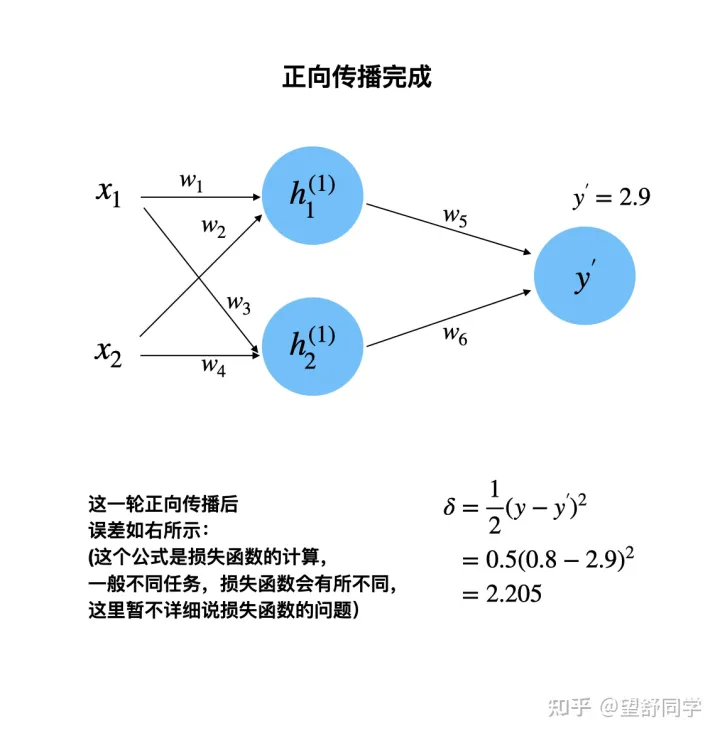
正向传播完成
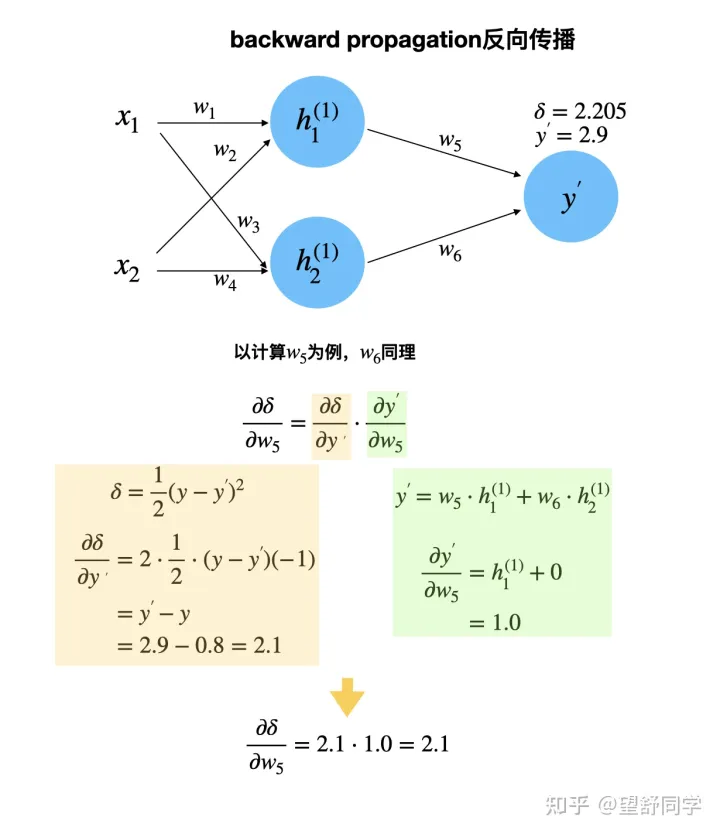
反向传播 第一次
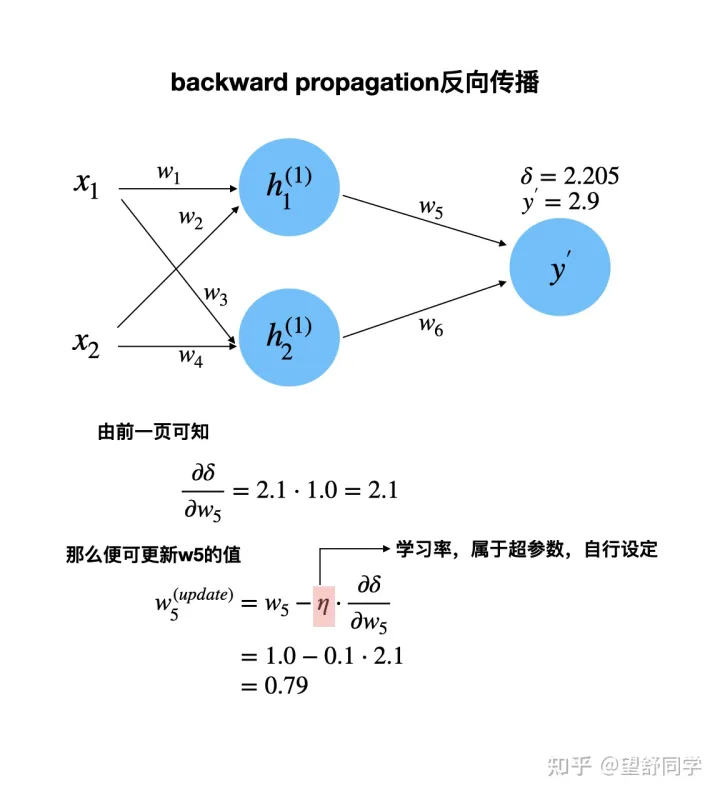
反向传播 第一次 数据更新
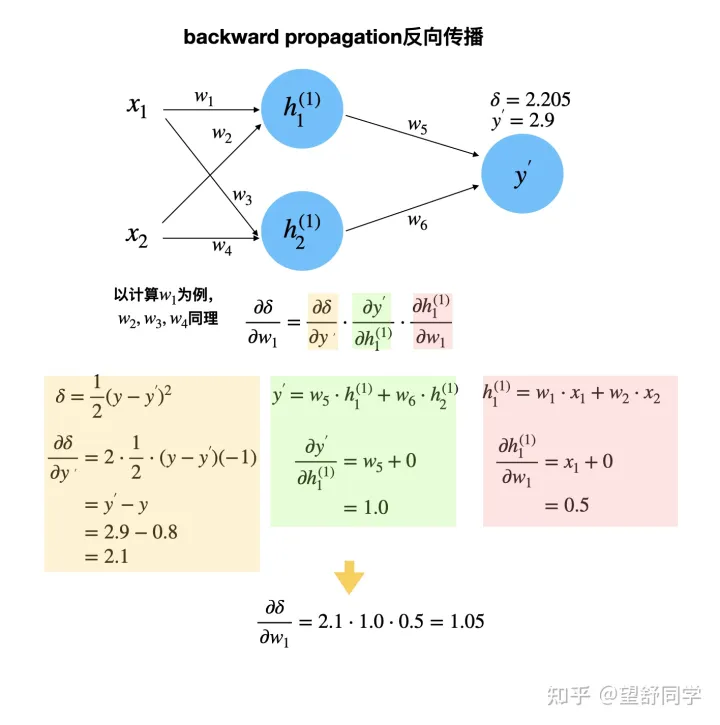
反向传播 其他数据
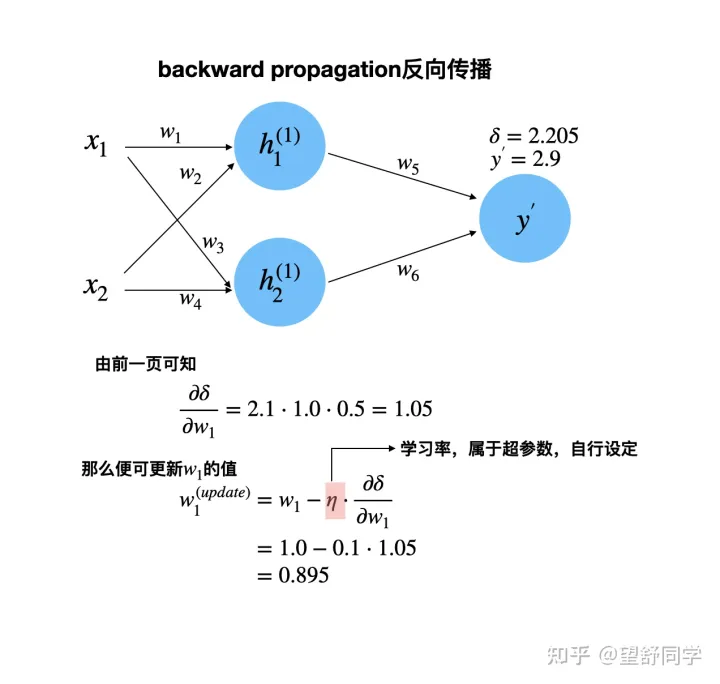
反向传播 最后一个数据
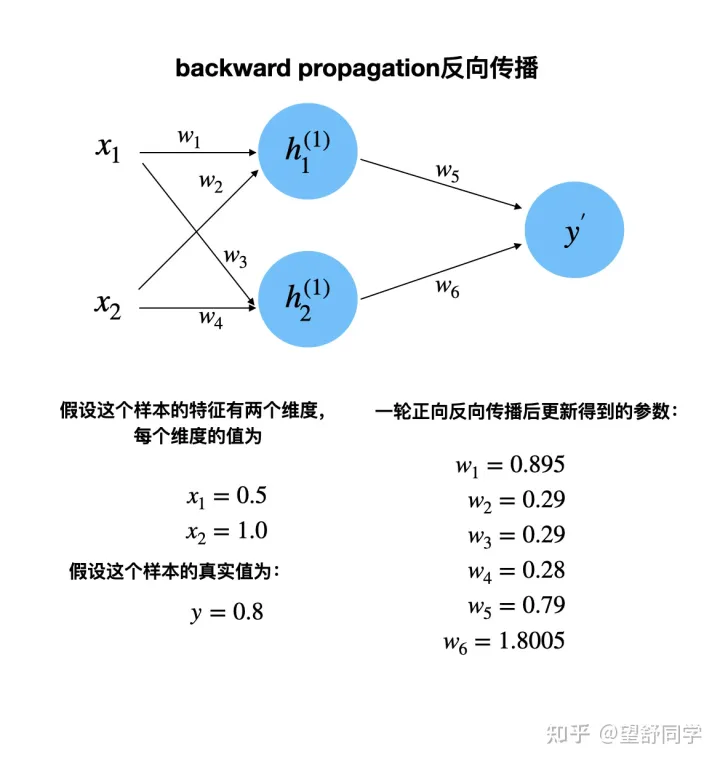
反向传播完成
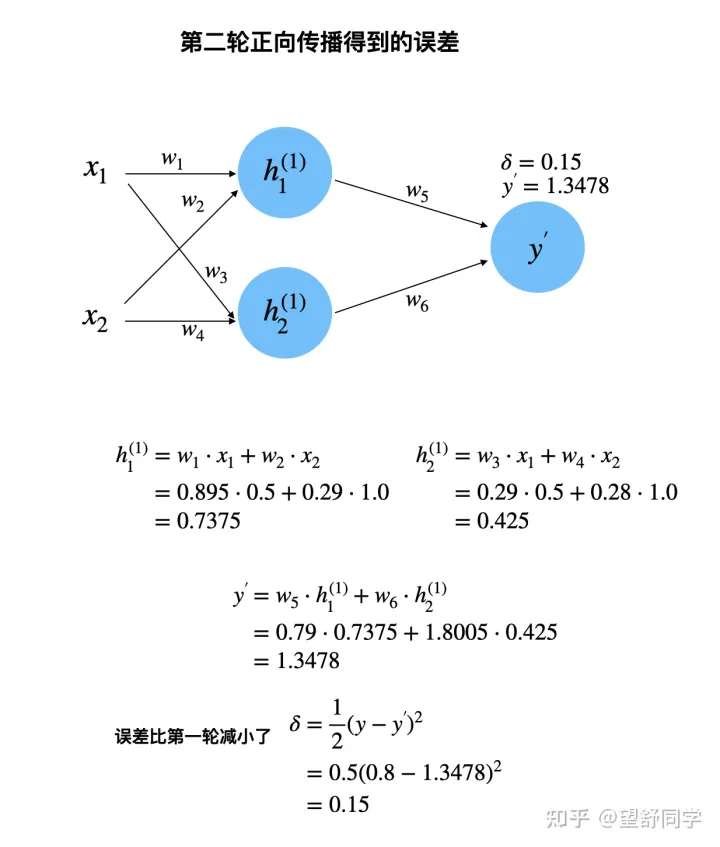
第二轮传播
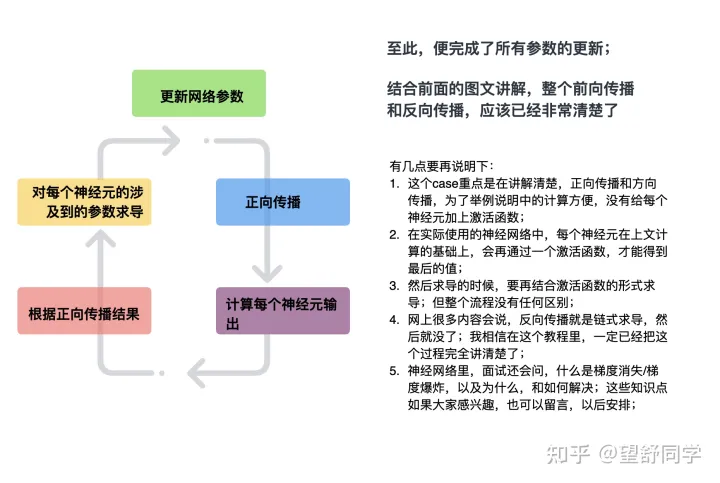
总结
9-4. 使用注意:展开参数 07:48
9-5. 梯度检测 11:38
梯度近似值: \(gradApprox = (J(\theta + \epsilon) – J(\theta - \epsilon)) / (2*\epsilon)\)
Implementation Note:
- Implement backprop to compute DVec (unrolled $D^{(1)}$, $D^{(2)}$, $D^{(3)}$).
- Implement numerical gradient check to compute gradApprox.
- Make sure they give similar values.
- Turn off gradient checking. Using backprop code for learning.
Important:
- Be sure to disable your gradient checking code before training your classifier. If you run numerical gradient computation on every iteration of gradient descent (or in the inner loop of costFunction(…))your code will be very slow.
9-6. 随机初始化 06:52
9-7. 组合到一起 13:24
网络结构:第一件要做的事是选择网络结构,即决定选择多少层以及决定每层分别有多少个单元。
第一层的单元数即我们训练集的特征数量。 最后一层的单元数是我们训练集的结果的类的数量。
如果隐藏层数大于 1,确保每个隐藏层的单元个数相同,通常情况下隐藏层单元的个数越多越好。 我们真正要决定的是隐藏层的层数和每个中间层的单元数。
训练神经网络:
- 参数的随机初始化
- 利用正向传播方法计算所有的 $h_{\theta}(x)$
- 编写计算代价函数 $J$ 的代码
- 利用反向传播方法计算所有偏导数
- 利用数值检验方法检验这些偏导数
- 使用优化算法来最小化代价函数
9-8. 无人驾驶 06:31
ALVINN ( Autonomous Land Vehicle In a Neural Network )是一个基于神经网络的智能系统,通过观察人类的驾驶来学习驾驶, ALVINN 能够控制 NavLab ,装在一辆改装版军用悍马,这辆悍马装载了传感器、计算机和驱动器用来进行自动驾驶的导航试验。 实现 ALVINN 功能的第一步,是对它进行训练,也就是训练一个人驾驶汽车。
10-1. 决定下一步做什么 05:51
10-2. 评估假设 07:36
评估是否过度拟合 为了检验算法是否过拟合,我们将数据分成训练集和测试集, 通常用 70% 的数据作为训练集,用剩下 30% 的数据作为测试集。 很重要的一点是训练集和测试集均要含有各种类型的数据, 通常我们要对数据进行“洗牌”,然后再分成训练集和测试集。
10-3. 模型选择和训练、验证、测试集 12:04
多个模型,怎么选择? 泛化能力。模型选择的方法为:
- 使用训练集训练出 10 个模型
- 用 10 个模型分别对交叉验证集计算得出交叉验证误差(代价函数的值)
- 选取代价函数值最小的模型
- 用步骤 3 中选出的模型对测试集计算得出推广误差(代价函数的值)
Train/validation/test error
Training error: \(J_{train}(\theta) = \frac{1}{2m}\sum_\limits{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2\)
Cross Validation error: \(J_{cv}(\theta) = \frac{1}{2m_{cv}}\sum_\limits{i=1}^{m}(h_{\theta}(x^{(i)}_{cv})-y^{(i)}_{cv})^2\)
Test error: \(J_{test}(\theta)=\frac{1}{2m_{test}}\sum_\limits{i=1}^{m_{test}}(h_{\theta}(x^{(i)}_{cv})-y^{(i)}_{cv})^2\)
10-4. 诊断偏差与方差 07:43
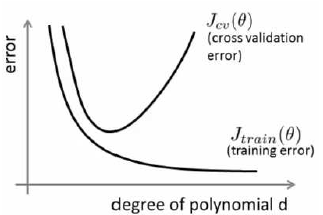
- 训练集误差和交叉验证集误差近似时:偏差 / 欠拟合
- 交叉验证集误差远大于训练集误差时:方差 / 过拟合
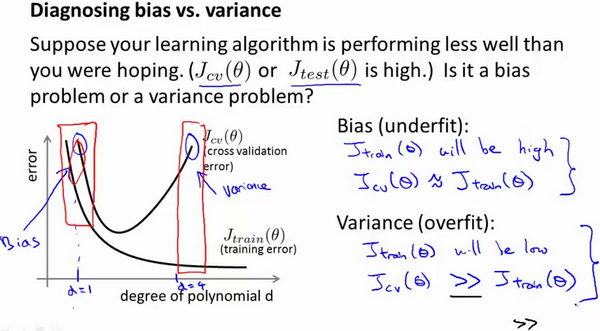
10-5. 正则化和偏差、方差 11:21

- 训练集误差和交叉验证集误差近似时:偏差 / 欠拟合
- 交叉验证集误差远大于训练集误差时:方差 / 过拟合
10-6. 学习曲线 11:54
10-7. 决定接下来做什么 06:51
- 获得更多的训练样本 —— 解决高方差
- 尝试减少特征的数量 —— 解决高方差
- 尝试获得更多的特征 —— 解决高偏差
- 尝试增加多项式特征 —— 解决高偏差
- 尝试减少正则化程度 λ —— 解决高偏差
- 尝试增加正则化程度 λ —— 解决高方差
11-1. 确定执行的优先级 09:30
垃圾邮件分类。
11-2. 误差分析 13:13
构建一个学习算法的推荐方法为:
- 从一个简单的能快速实现的算法开始,实现该算法并用交叉验证集数据测试这个算法
- 绘制学习曲线,决定是增加更多数据,或者添加更多特征,还是其他选择
- 进行误差分析:人工检查交叉验证集中我们算法中产生预测误差的样本,看看这些样本是否有某种系统化的趋势
11-3. 不对称性分类的误差评估 11:36
偏斜类。
查准率。 召回率。
查准率 ( Precision )和 查全率 ( Recall ) 我们将算法预测的结果分成四种情况:
- 正确肯定 ( True Positive, TP ):预测为真,实际为真
- 正确否定 ( True Negative, TN ):预测为假,实际为假
- 错误肯定 ( False Positive, FP ):预测为真,实际为假(假阳性)
- 错误否定 ( False Negative, FN ):预测为假,实际为真(假阴性)
则:查准率 = TP/(TP+FP) 。例,在所有我们预测有恶性肿瘤的病人中,实际上有恶性肿瘤的病人的百分比,越高越好。
查全率 = TP/(TP+FN) 。例,在所有实际上有恶性肿瘤的病人中,成功预测有恶性肿瘤的病人的百分比,越高越好。
这样,对于我们刚才那个总是预测病人肿瘤为良性的算法,其查全率是 0。
| 预测值 | |||
|---|---|---|---|
| Positive | Negtive | ||
| 实际值 | Positive | TP | FN |
| Negtive | FP | TN |
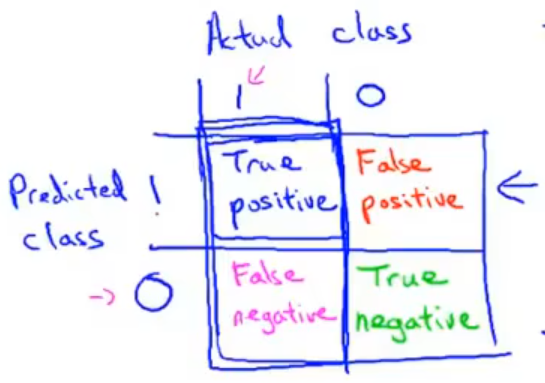
11-4. 精确度和召回率的权衡 14:06
$F_1$ Score (F score)
\[2\frac{PR}{P+R}\]11-5. 机器学习数据 11:10

- 参数多,特征多,保证低偏差。
- 数据样本多,就不太可能过拟合,保证低方差。
这是一个关键的假设:特征值有足够的信息量,且我们有一类很好的函数,这是为什么能保证低误差的关键所在。它有大量的训练数据集,这能保证得到更多的方差值,因此这给我们提出了一些可能的条件,如果你有大量的数据,而且你训练了一种带有很多参数的学习算法,那么这将会是一个很好的方式,来提供一个高性能的学习算法。
12-1. 优化目标 14:48
SVM Support Vector Machine
- 线性回归算法 Linear Regression
- 支持向量机算法 (Support Vector Machine, SVM)
- 最近邻居 / k-近邻算法 (K-Nearest Neighbors, KNN)
- 逻辑回归算法 Logistic Regression
- 决策树算法 Decision Tree
- k-平均算法 K-Means
- 随机森林算法 Random Forest
- 朴素贝叶斯算法 Naive Bayes
- 降维算法 Dimensional Reduction
- 梯度增强算法 Gradient Boosting
Boosting 和 AdaBoost Boosting 是一种集成技术,它试图从多个弱分类器中创建一个强分类器。 妈妈卡号 邮政 2080
12-2. 直观上对大间隔的理解 10:37
12-3. 大间隔分类器的数学原理 19:42
向量内积(点乘)的定义及几何意义
向量内积:一个向量在另外一个向量上的投影。 即:某个方向力 u,在 v 方向上的分量。结果是一个标量(无方向)。
12-4. 核函数 1 15:45
个人理解: 定义多个标记点,通过 kernal 函数 映射到另外一个空间 解决问题。
12-5. 核函数 2 15:44
12-6. 使用 SVM 21:03
liblinear libsvm
More esoteric: String kernel, chi-square kernel, histogram intersection kernel, … 字符串距离,卡方核函数,直方相交核函数。
sklearn 包括了分类,回归,降维和聚类等四大机器学习算法,还包括了特征提取,数据处理和模型评估者三大模块。 sk-learn 库,基于上述的 numpy 和 Scipy 的库。包含大量用于传统机器学习和数据挖掘相关的算法,集成了常见的机器学习功能。 Scikit-learn 主要用于各种数据建模概念,如回归、分类、聚类、模型选择等。 该库是在 Numpy、Scipy 和 matplotlib 之上编写的。Scikit-learn 易于集成,可以继承其他机器学习库实现特定目标。 比如 Numpy 和 Pandas 用于数据分析,Plotly 用于可视化。
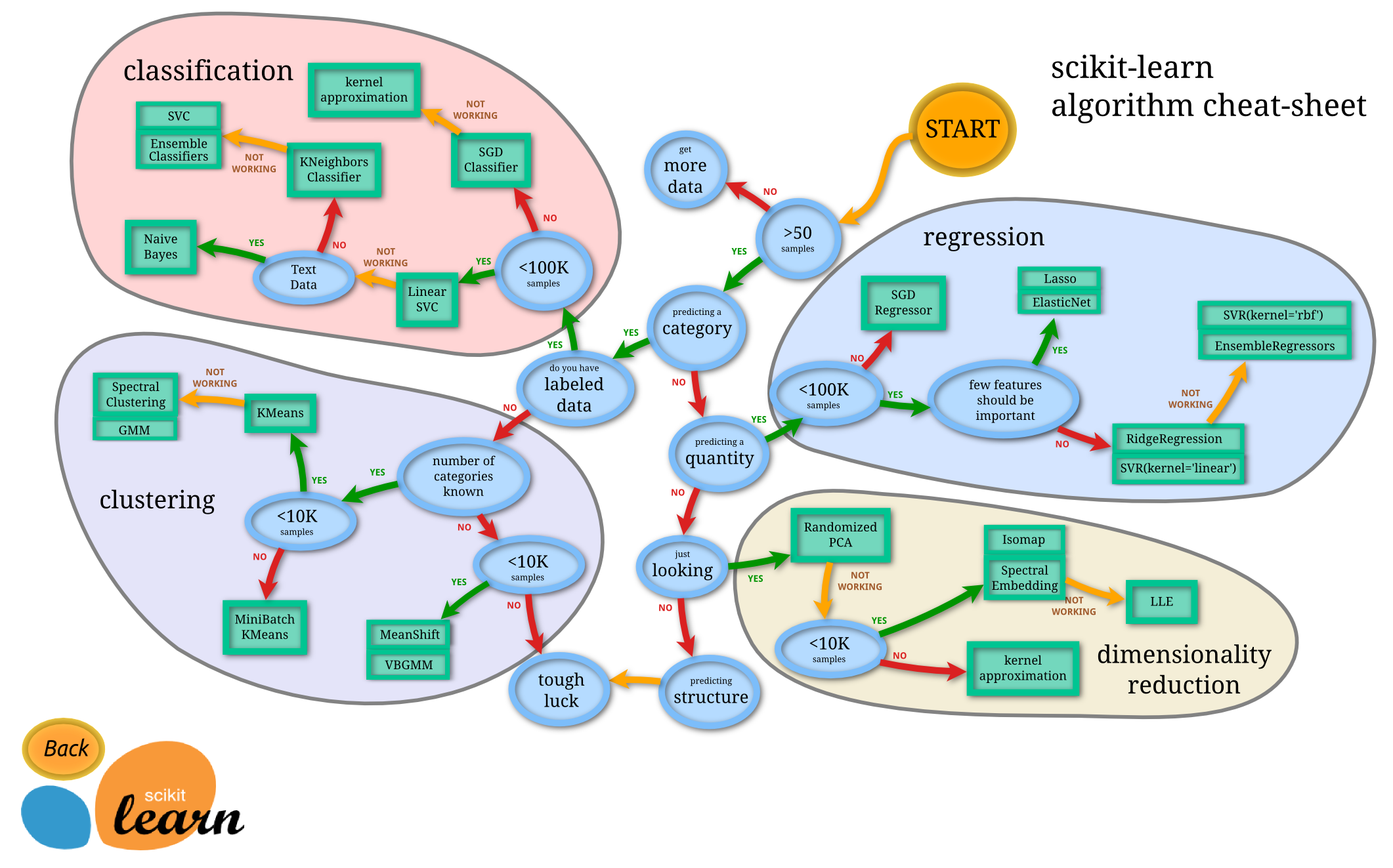
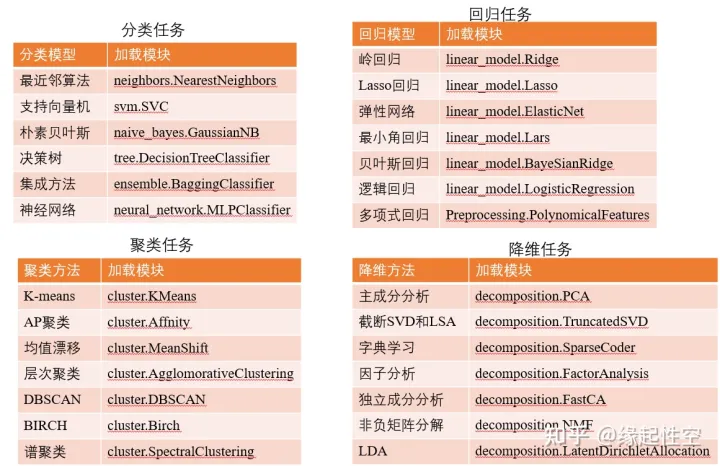
- sklearn 库主要模块功能和辅助函数
- sklearn 库机器学习 python 使用教程

- 1、分类学习 (classification),属于监督型
- 适用算法一:k 邻算法
- 适用算法二:支持向量机 (SVC)
- 2、回归学习 (regression),属于监督型
- 适用算法一:线性回归法
- 适用算法二:支持向量机 (SVR)
- 3、聚类学习 (clustering),不属于监督型
- 4、降维学习 (dimensionality reduction) 不属于监督型
- 1、分类学习 (classification),属于监督型
imgaug :机器学习实验中的图像增强库,特别是卷积神经网络。支持以多种不同方式增强图像、关键点 / 地标、边界框、热图和分割图。 Image augmentation for machine learning experiments.
下面是一些普遍使用的准则:
$n$ 为特征数,$m$ 为训练样本数。
- 如果相较于 $m$ 而言,$n$ 要大许多,即训练集数据量不够支持我们训练一个复杂的非线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。
- 如果 $n$ 较小,而且 $m$ 大小中等,例如 $n$ 在 1-1000 之间,而 $m$ 在 10-10000 之间,使用高斯核函数的支持向量机。
- 如果 $n$ 较小,而 $m$ 较大,例如 $n$ 在 1-1000 之间,而 $m$ 大于 50000,则使用支持向量机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
13-1. 无监督学习 03:18
13-2. K-Means 算法 12:33
从上面的分析可以看出,k-means 是随机的分配 k 个初始聚类中心。而聚类的结果高度依赖质心的初始化。如果初始聚类中心选的不好,k-means 算法最终会收敛到一个局部最优值,而不是全局最优值。为了解决这个问题,引入了 k-means++ 算法,它的基本思想就是:初始的聚类中心之间的相互距离要尽可能的远。而且在计算过程中,我们通常采取的措施是进行不止一次的聚类,每次都初始化不同的中心,以 inertial 最小的聚类结果作为最终聚类结果。
pyclusring 库下的 kmeans 聚类
13-3. 优化目标 07:05
13-4. 随机初始化 07:50
13-5. 选取聚类数量 08:23
常见的一种方法是 elbow method,x 轴为聚类的数量,y 轴为 WSS(within cluster sum of squares)也就是各个点到 cluster 中心的距离的平方的和。https://www.zhihu.com/question/29208148
对于 K-means 中 K 的选择,通常有 四种方法:
- 按需选择
- 观察法
- 手肘法
- Gap Statistics 方法
14-1. 目标 I:数据压缩 10:10
数据降维。投影。
14-2. 目标 II:可视化 05:28
数据可视化。
14-3. 主成分分析问题规划 1 09:06
主成分分析(PCA)
PCA is not linear regression
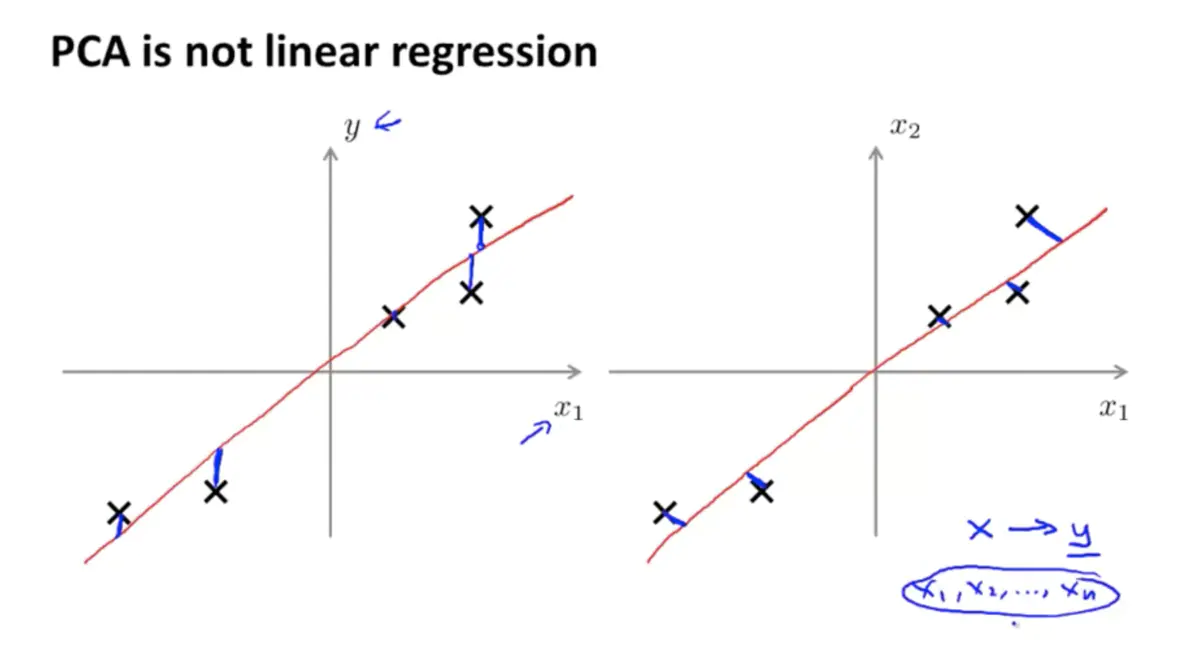
线性回归的 Cost function 重点在回归值和真实值的误差,而 PCA 着重样本与超平面的投影距离。
PCA 减少 $n$ 维到 $k$ 维:
第一步是均值归一化。我们需要计算出所有特征的均值,然后令 $x_j= x_j-μ_j$。如果特征是在不同的数量级上,我们还需要将其除以标准差 $σ^2$。
第二步是计算 协方差矩阵 ( covariance matrix )$Σ$: $\sum=\dfrac {1}{m}\sum^{n}_{i=1}\left( x^{(i)}\right) \left( x^{(i)}\right) ^{T}$
第三步是计算协方差矩阵 $Σ$ 的 特征向量 ( eigenvectors ):
在 Octave 里我们可以利用 奇异值分解 ( singular value decomposition )来求解, [U, S, V]= svd(sigma) 。
对于一个 $n×n$ 维度的矩阵,上式中的 $U$ 是一个具有与数据之间最小投射误差的方向向量构成的矩阵。如果我们希望将数据从 $n$ 维降至 $k$ 维,我们只需要从 $U$ 中选取前 $k$ 个向量,获得一个 $n×k$ 维度的矩阵,我们用 $U_{reduce}$ 表示,然后通过如下计算获得要求的新特征向量 $z^{(i)}$: \(z^{(i)}=U^{T}_{reduce}*x^{(i)}\)
其中 $x$ 是 $n×1$ 维的,因此结果为 $k×1$ 维度。注,我们不对方差特征进行处理。
14-4. 主成分分析问题规划 2 15:15
14-5. 主成分数量选择 10:31
方差检查,保留到 99%。 我们可以使用这个矩阵来计算平均均方误差与训练集方差的比例: \(\dfrac {\dfrac {1}{m}\sum^{m}_{i=1}\left\| x^{\left( i\right) }-x^{\left( i\right) }_{approx}\right\| ^{2}}{\dfrac {1}{m}\sum^{m}_{i=1}\left\| x^{(i)}\right\| ^{2}}=1-\dfrac {\Sigma^{k}_{i=1}S_{ii}}{\Sigma^{m}_{i=1}S_{ii}}\leq 1\%\)
也就是:\(\frac {\Sigma^{k}_{i=1}s_{ii}}{\Sigma^{n}_{i=1}s_{ii}}\geq0.99\)
在压缩过数据后,我们可以采用如下方法来近似地获得原有的特征:\(x^{\left( i\right) }_{approx}=U_{reduce}z^{(i)}\)
PCA 跟 傅里叶变换 有点神似,开始是低频,然后是高频。SVD 是 PCA 的一个快速算法求解实现。 傅里叶变换,PCA、SVD,从数学上来说都是矩阵变换,从一个矩阵乘以一个变换矩阵变为另一个矩阵,由于变换矩阵一般都具有特殊性,达到升降维的作用。从矩阵的角度来说都是基变换,就是从一个坐标系转换到另一个坐标系,坐标系维度也会发生变换。从应用角度来说,傅里叶变换其实是通过那个复杂的傅里叶变换函数产生无限个正交基,从而起到升维目的(记得是 1、cos、sin)这样信号中很多看不出来的东西就全部能看出来了,而 SVD、PCA 是反过程,特征太多了,但是有很多是没用的,只需要主要特征就可以了,这样求出特征值,压缩一下就好了。相当于 sift 中的尺度不变性吧,一个物体如果离得比较近,用小的高斯卷积核去平滑,这样细节更多了,相当于傅里叶变换了,这样很多细小的细节都能体现出来,分析起来就很容易了,但是有时候只需要整体把握就可以,那就要大点的卷积核去滤波,相当于站的比较远,这样细节就没了,相当于用 PCA 了,如果大的卷积核卷积仍然能看清的东西,那就是主要特征了吧。图像表征:离散傅里叶变换(DFT)、离散余弦变换(DCT)、主成分分析(PCA)。
14-6. 压缩重现 03:55
14-7. 应用 PCA 的建议 12:49
错误的主要成分分析情况:一个常见错误使用主要成分分析的情况是,将其用于减少过拟合(减少了特征的数量)。这样做非常不好,不如尝试正则化处理。
另一个常见的错误是,默认地将主要成分分析作为学习过程中的一部分,这虽然很多时候有效果,最好还是从所有原始特征开始,只在有必要的时候(算法运行太慢或者占用太多内存)才考虑采用主要成分分析。
古希腊几何学家阿波洛尼乌斯总结了圆锥曲线理论,一千八百年后德国天文学家开普勒将其应用于行星轨道理论。伽罗华公元 1831 年创立群论,一百多年后获得物理应用。公元 1860 年创立的矩阵理论在六十年后应用量子力学。数学家莱姆伯脱,高斯,黎曼,罗马切夫斯基等人提出并发展了非欧几何,高斯一生都在探索非欧几何的实际应用,但他抱憾而终。非欧几何诞生一百七十年后,这种在当时毫无用处的理论以及由之发展而来的张量分析理论成为爱因斯坦广义相对论的核心基础。世界沉默了,为了这些伤心的名字,为了这些伤心的名字后面那千百年的寂寞时光。
- P 类问题
- P 问题是初始问题,所有这类问题都可以用一个确定性算法在多项式时间内求出解。
- NP(Non-deterministic Polynomial,即多项式复杂程度的非确定性问题)问题
- NP 问题,能够多项式时间求得解,或者多项式时间内判断是否是正确的,P 包含于 NP。
- NP 完全问题(NPC)
- NPC 问题,全部 NP 问题在多项式时间内,可以约化到的问题,NPC 包含于 NP。
- NP-hard 问题(NPH,NP 困难问题)
- NPH 问题,NPC 问题在多项式时间内,可以约化到的问题,NPC 包含于 NPH,但 NPC 与 NP 和 P 无必然联系。
15-1. 问题动机 07:39
异常检测。
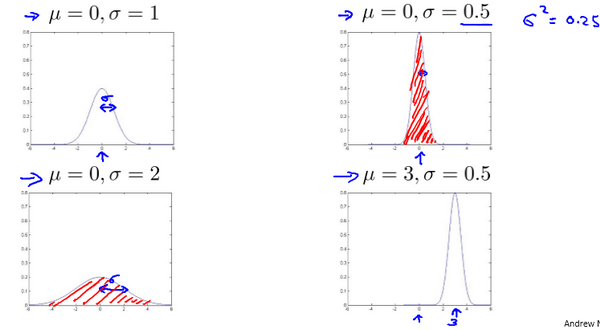
15-2. 高斯分布 10:28
\[f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{z^2}{2}}=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]通常如果我们认为变量 $x$ 符合高斯分布 $x \sim N(\mu, \sigma^2)$ 则其概率密度函数为: $p(x,\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$ 我们可以利用已有的数据来预测总体中的 $μ$ 和 $σ^2$ 的计算方法如下: $\mu=\frac{1}{m}\sum\limits_{i=1}^{m}x^{(i)}$
$\sigma^2=\frac{1}{m}\sum\limits_{i=1}^{m}(x^{(i)}-\mu)^2$
15-3. 算法 12:03
对于给定的数据集 $x^{(1)},x^{(2)},…,x^{(m)}$,我们要针对每一个特征计算 $\mu$ 和 $\sigma^2$ 的估计值。
$\mu_j=\frac{1}{m}\sum\limits_{i=1}^{m}x_j^{(i)}$
$\sigma_j^2=\frac{1}{m}\sum\limits_{i=1}^m(x_j^{(i)}-\mu_j)^2$
一旦我们获得了平均值和方差的估计值,给定新的一个训练实例,根据模型计算 $p(x)$:
$p(x)=\prod\limits_{j=1}^np(x_j;\mu_j,\sigma_j^2)=\prod\limits_{j=1}^1\frac{1}{\sqrt{2\pi}\sigma_j}exp(-\frac{(x_j-\mu_j)^2}{2\sigma_j^2})$
当 $p(x) < \varepsilon$ 时,为异常。
15-4. 开发和评估异常检测系统 13:08
15-5. 异常检测 VS 监督学习 07:37
| 异常检测 | 监督学习 |
|---|---|
| 非常少量的正向类(异常数据 $y=1$), 大量的负向类($y=0$) | 同时有大量的正向类和负向类 |
| 许多不同种类的异常,非常难。根据非常 少量的正向类数据来训练算法。 | 有足够多的正向类实例,足够用于训练 算法,未来遇到的正向类实例可能与训练集中的非常近似。 |
| 未来遇到的异常可能与已掌握的异常、非常的不同。 | |
| 例如: 欺诈行为检测 生产(例如飞机引擎)检测数据中心的计算机运行状况 | 例如:邮件过滤器 天气预报 肿瘤分类 |
15-6. 选择要使用的功能 12:18
15-7. 多变量高斯分布 13:47
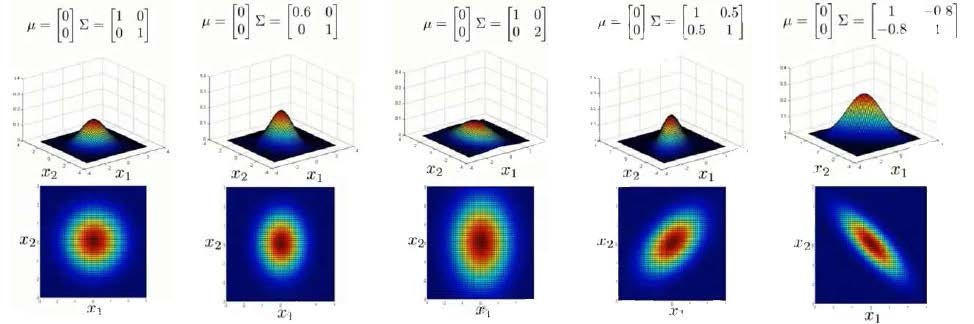
读 mu and sigma。 这玩意就是变换矩阵,对特征进行缩放拉伸。
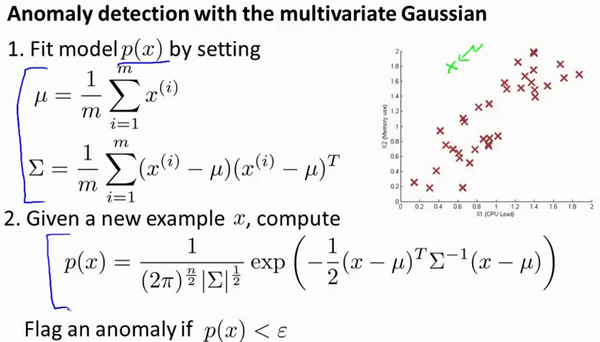
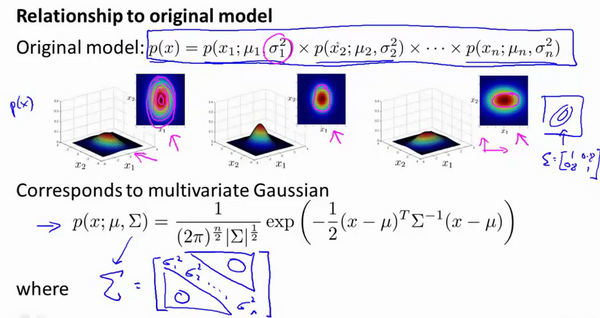
15-8. 使用多变量高斯分布的异常检测 14:04
16-1. 问题规划 07:55
16-2. 基于内容的推荐算法 14:32
假设我们采用线性回归模型,我们可以针对每一个用户都训练一个线性回归模型,如 ${ {\theta }^{(1)}}$ 是第一个用户的模型的参数。 于是,我们有:
$\theta^{(j)}$ 用户 $j$ 的参数向量
$x^{(i)}$ 电影 $i$ 的特征向量
对于用户 $j$ 和电影 $i$,我们预测评分为:$(\theta^{(j)})^T x^{(i)}$
代价函数
针对用户 $j$,该线性回归模型的代价为预测误差的平方和,加上正则化项: \(\min_{\theta (j)}\frac{1}{2}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2+\frac{\lambda}{2}\left(\theta_{k}^{(j)}\right)^2\)
其中 $i:r(i,j)$ 表示我们只计算那些用户 $j$ 评过分的电影。在一般的线性回归模型中,误差项和正则项应该都是乘以 $1/2m$,在这里我们将 $m$ 去掉。并且我们不对方差项 $\theta_0$ 进行正则化处理。
上面的代价函数只是针对一个用户的,为了学习所有用户,我们将所有用户的代价函数求和: \(\min_{\theta^{(1)},...,\theta^{(n_u)}} \frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2\) 如果我们要用梯度下降法来求解最优解,我们计算代价函数的偏导数后得到梯度下降的更新公式为:
\[\theta_k^{(j)}:=\theta_k^{(j)}-\alpha\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x_{k}^{(i)} \quad (\text{for} \, k = 0)\] \[\theta_k^{(j)}:=\theta_k^{(j)}-\alpha\left(\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x_{k}^{(i)}+\lambda\theta_k^{(j)}\right) \quad (\text{for} \, k\neq 0)\]16-3. 协同过滤 10:15
-
初始 $x^{(1)},x^{(1)},…x^{(nm)},\ \theta^{(1)},\theta^{(2)},…,\theta^{(n_u)}$ 为一些随机小值
-
使用梯度下降算法最小化代价函数
-
在训练完算法后,我们预测 $(\theta^{(j)})^Tx^{(i)}$ 为用户 $j$ 给电影 $i$ 的评分
通过这个学习过程获得的特征矩阵包含了有关电影的重要数据,这些数据不总是人能读懂的,但是我们可以用这些数据作为给用户推荐电影的依据。
16-4. 协同过滤算法 08:28
协同过滤优化目标:
给定 $x^{(1)},…,x^{(n_m)}$,估计 $\theta^{(1)},…,\theta^{(n_u)}$: \(\min_{\theta^{(1)},...,\theta^{(n_u)}}\frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2\)
给定 $\theta^{(1)},…,\theta^{(n_u)}$,估计 $x^{(1)},…,x^{(n_m)}$:
同时最小化 $x^{(1)},…,x^{(n_m)}$ 和 $\theta^{(1)},…,\theta^{(n_u)}$: \(J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)})=\frac{1}{2}\sum_{(i,j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(i)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2\)
\[\min_{x^{(1)},...,x^{(n_m)} \\\ \theta^{(1)},...,\theta^{(n_u)}}J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)})\]16-5. 矢量化:低轶矩阵分解 08:29
如果一位用户正在观看电影 $x^{(i)}$,我们可以寻找另一部电影 $x^{(j)}$,依据两部电影的特征向量之间的距离 $\left| { {x}^{(i)}}-{ {x}^{(j)}} \right|$ 的大小。
16-6. 实施细节:均值规范化 08:32
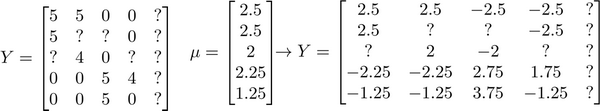
17-1. 学习大数据集 05:46
首先应该做的事是去检查一个这么大规模的训练集是否真的必要,也许我们只用 1000 个训练集也能获得较好的效果,我们可以绘制学习曲线来帮助判断。
17-2. 随机梯度下降 13:20
17-3. Mini-Batch 梯度下降 06:19
小批量梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法,每计算常数 $b$ 次训练实例,便更新一次参数 ${ {\theta }}$ 。
通常我们会令 $b$ 在 2-100 之间。这样做的好处在于,我们可以用向量化的方式来循环 $b$ 个训练实例,如果我们用的线性代数函数库比较好,能够支持平行处理,那么算法的总体表现将不受影响(与随机梯度下降相同)。
17-4. 随机梯度下降收敛 11:32
17-5. 在线学习 12:51
17-6. 减少映射与数据并行 14:09
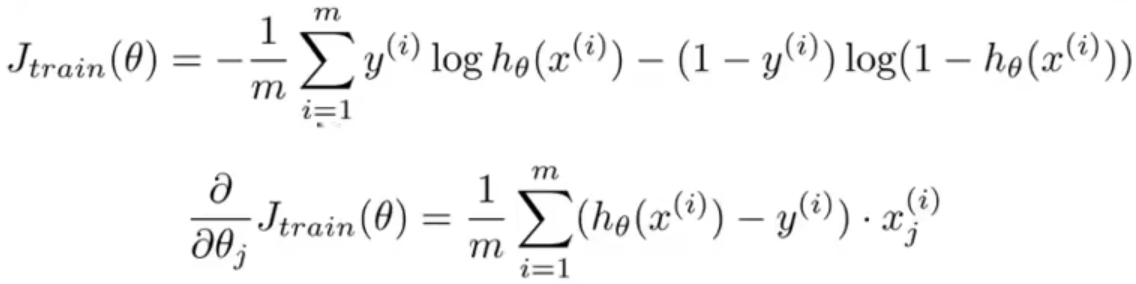
18-1. 问题描述与 OCR pipeline 07:03
- 文字侦测( Text detection ) —— 将图片上的文字与其他环境对象分离开来
- 字符切分( Character segmentation ) —— 将文字分割成一个个单一的字符
- 字符分类( Character classification ) —— 确定每一个字符是什么
可以用任务流程图来表达这个问题,每一项任务可以由一个单独的小队来负责解决:

18-2. 滑动窗口 14:41
18-3. 获取大量数据和人工数据 16:21
有关获得更多数据的几种方法:
- 人工数据合成
- 手动收集、标记数据
- 众包
18-4. 天花板分析:下一步工作的 pipeline 13:51
19-1. 总结与感谢 04:43
最后,在结束之前,我还想再多说一点:那就是,也许不久以前我也是一个学生,即使是现在,我也尽可能挤出时间听一些课,学一些新的东西。所以,我深知要坚持学完这门课是很需要花一些时间的,我知道,也许你是一个很忙的人,生活中有很多很多事情要处理。正因如此,你依然挤出时间来观看这些课程视频。我知道,很多视频的时间都长达数小时,你依然花了好多时间来做这些复习题。你们中好多人,还愿意花时间来研究那些编程练习,那些又长又复杂的编程练习。我对你们表示衷心的感谢!我知道你们很多人在这门课中都非常努力,很多人都在这门课上花了很多时间,很多人都为这门课贡献了自己的很多精力。所以,我衷心地希望你们能从这门课中有所收获!
最后我想说!再次感谢你们选修这门课程!
Andew Ng
参考资料快照
- https://mp.weixin.qq.com/s?__biz=MzU2NTUwNjQ1Mw==&mid=2247485091&idx=1&sn=8844a2dfafcd35ea45d1bf0146ba8a5a&chksm=fcbbfe59cbcc774f68a18bd11d529422e0048896ffa3a253c52a749fc6e45d7292e1791052da&scene=27
- https://www.bilibili.com/video/BV164411b7dx/
- https://www.coursera.org/specializations/deep-learning
- https://www.coursera.org/learn/machine-learning-course/home/week/1
- https://space.bilibili.com/388675845
- https://www.bilibili.com/video/BV1Kh411X7Qv/
- https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
- http://www.ai-start.com/ml2014/
- https://scruel.github.io/Notes-ML-AndrewNg/
- https://www.jianshu.com/p/682c88cee5a8
- https://cs.nyu.edu/~roweis/kica.html
- https://www.octave.org/
- https://cloud.tencent.com/developer/article/1650390
- https://octave.sourceforge.io/symbolic/index.html
- https://zhuanlan.zhihu.com/p/89074979
- https://docs.microsoft.com/zh-cn/azure/machine-learning/component-reference/one-vs-all-multiclass
- https://zhuanlan.zhihu.com/p/410358244
- https://zhuanlan.zhihu.com/p/464268270
- https://www.bilibili.com/video/BV1QV4y1E7eA/
- https://blog.csdn.net/qq_39783601/article/details/123365469
- https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html
- https://www.bilibili.com/read/cv12252018/
- https://blog.csdn.net/weixin_51111267/article/details/122628057
- https://imgaug.readthedocs.io/en/latest/
- https://www.zhihu.com/question/29208148
- http://sofasofa.io/forum_main_post.php?postid=1000282
- 机器学习 -- 大型语言模型简史:从 Transformers (2017) 到 DeepSeek-R1(2025) | 20 Feb 2025
- 机器学习 -- DALL·E 2 & 扩散模型 | 21 Dec 2024
- 机器学习 -- 学术论文解读系列(进行中) | 04 Oct 2024
- 机器学习 -- 经典论文 ViT (Vision Transformer) | 24 Jul 2024
- 机器学习 -- 跟李沐学 AI【论文精读】(进行中) | 09 Jul 2024
- 机器学习 -- Attention is all you need | 30 Jun 2024
- 机器学习笔记 -- 3Blue1Brown 深度学习 Deep Learning(已完成) | 29 Jun 2024
- 机器学习 -- 李宏毅 2021/2022 春机器学习课程(进行中) | 31 Aug 2023
- 机器学习 -- 实用机器学习 李沐(进行中) | 31 Aug 2023
- 机器学习 -- ChatGPT Prompt 提示词 吴恩达(进行中) | 28 Jul 2023
- 机器学习 -- 浙江大学 · 机器学习(已完成) | 12 Feb 2023
- 机器学习 -- 人工智能学习路线(进行中……) | 10 Feb 2023
- 机器学习 -- 北交 / 图像处理与机器学习(已完成) | 03 Dec 2022
- 机器学习笔记 -- 人工智能 机器学习 算法概览(已完成) | 13 Oct 2022
- 机器学习笔记 -- 神经网络内部发生了什么?深度学习可视化 | 13 Oct 2022
- 机器学习 -- 吴恩达机器学习 Review(已完成) | 31 Aug 2022
- 机器学习 -- 吴恩达深度学习(进行中) | 31 Aug 2022
- 机器学习 -- 吴恩达机器学习(已完成) | 31 Aug 2022
- 机器学习笔记 -- 神经网络和深度学习简史 | 26 Dec 2020


 .
.