机器学习笔记 -- 神经网络和深度学习简史
Andrey Kurenkov
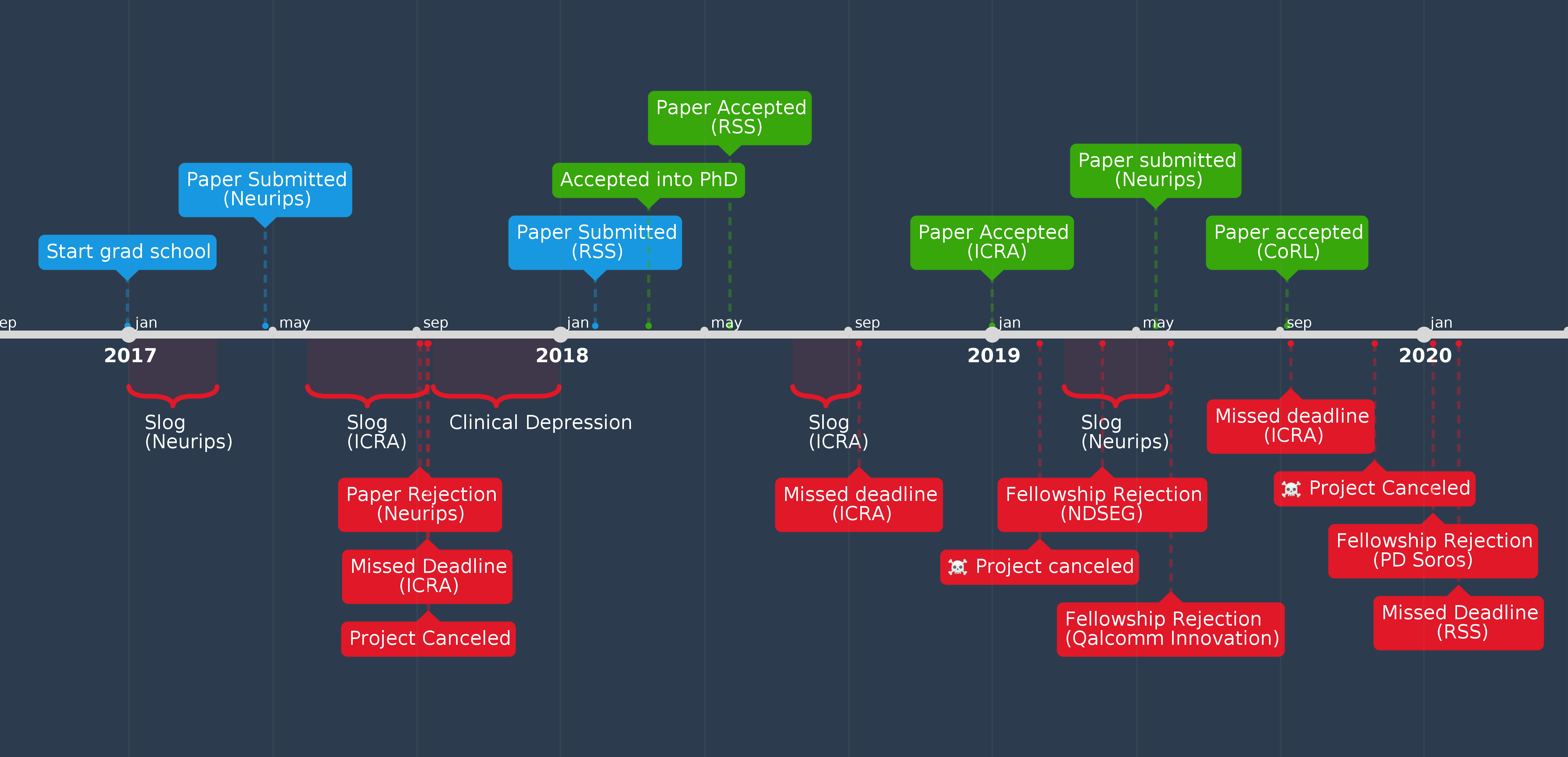
人工智能依然不会思考,但依靠亿万次运算也足够在很多工作上处理地比大多数人更好。人们讨论的新问题是,人工智能会不会强化偏见。
基哥视频有更详细的讲解。
浙江大学 · 机器学习
从感知机到 BP 算法 (1950s-1980s)
线性回归
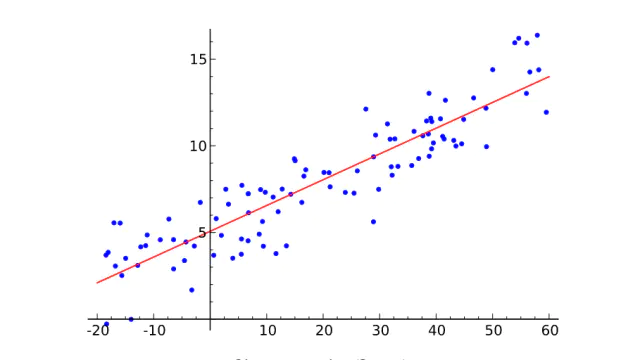
虚假承诺的荒唐
弗兰克 · 罗森布拉特 (Frank Rosenblatt) 的感知机 Perceptron。
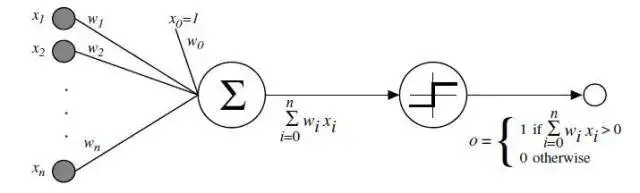
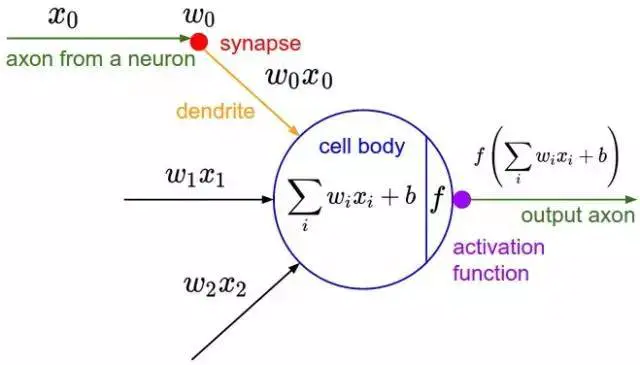
算法如下:
- 从感知机有随机的权重和一个训练集开始。
- 对于训练集中一个实例的输入值,计算感知机的输出值。
- 如若感知机的输出值和实例中默认正确的输出值不同:
- 若输出值应该为 0 但实际为 1,减少输入值是 1 的例子的权重。
- 若输出值应该为 1 但实际为 0,增加输入值是 1 的例子的权重。
- 对于训练集中下一个例子做同样的事,重复步骤 2-4 直到感知机不再出错。

康奈尔航天实验室的 Mark I 感知机,第一台感知机的硬件
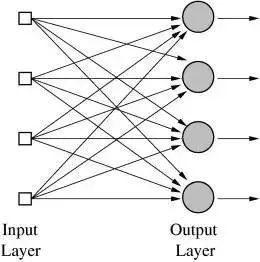
多层输出的神经网络
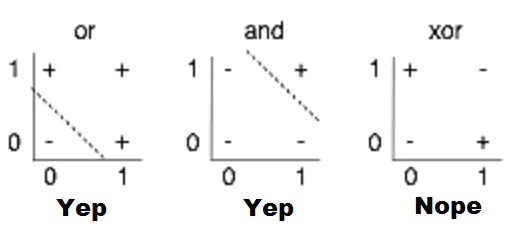
感知机局限性的视觉化。找到一个线性函数,输入 X,Y 时可以正确地输出 + 或 -,就是在 2D 图表上画一条从 + 中分离出 - 的线;很显然,就第三幅图显示的情况来看,这是不可能的。
人工智能冬天的复苏
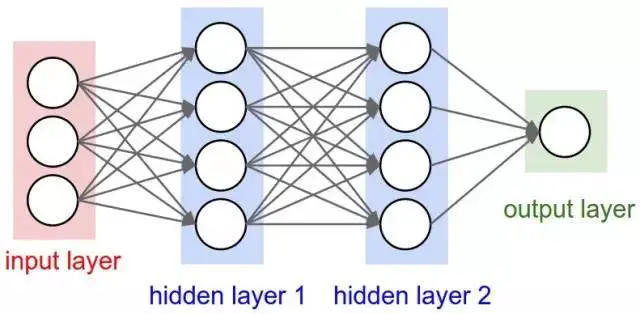
有两个隐藏层的神经网络
多个隐藏层是件好事,原因在于隐藏层可以找到数据内在特点,后续层可以在这些特点(而不是嘈杂庞大的原始数据)基础上进行操作。
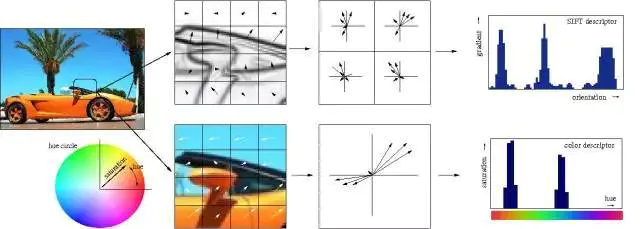
传统的特征的手工提取过程的视觉化
我们可以利用微积分将一些导致输出层任何训练集误差的原因分配给前一隐藏层的每个神经元,如果还有另外一层隐藏层,我们可以将这些原因再做分配,以此类推 —— 我们在反向传播这些误差。 典型的随机梯度下降,找出最小化误差的最佳权值。
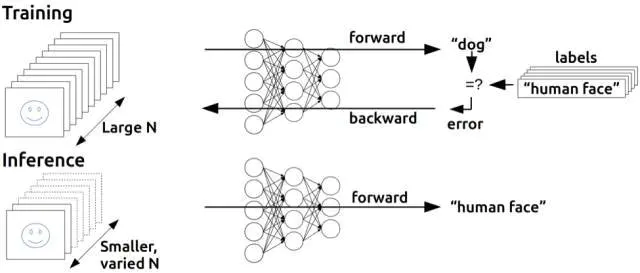
反向传播的基本思想
BP 算法之后的又一突破 —— 信念网络 (1980s-2000s)
神经网络获得视觉
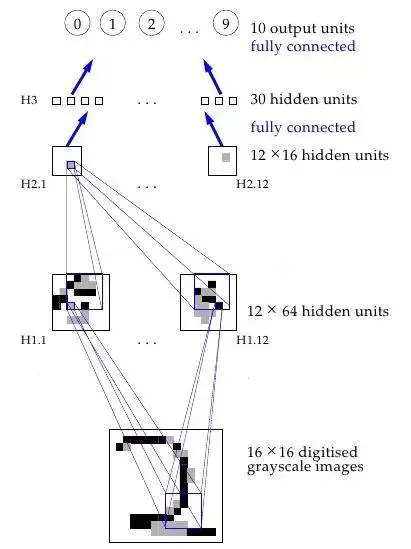
一个神经网络工作原理的可视化过程
多加了这两层 —— (卷积层和汇集层) —— 是卷积神经网络(CNNs/ConvNets)和普通旧神经网络的主要区别。
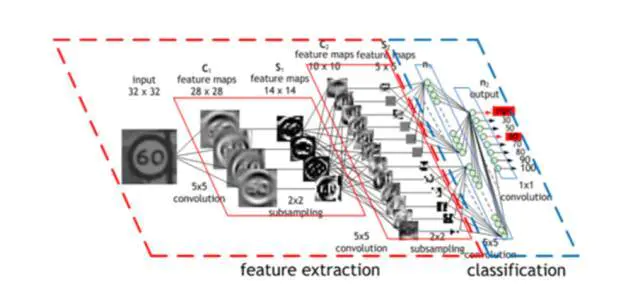
卷积神经网络(CNN)的操作过程
神经网络进入无监督学习时期
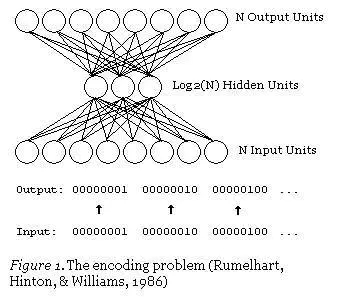
自编码神经网络

更明确地了解自编码压缩
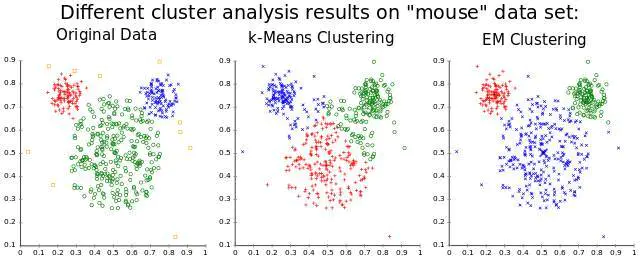
聚类,一种很常用的非监督式学习应用
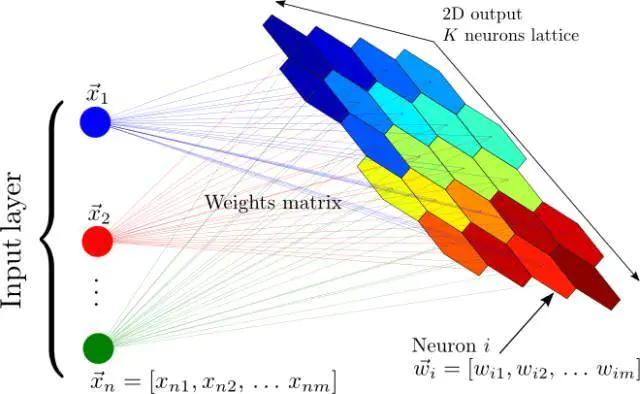
自组织映射神经网络
自组织映射神经网络:将输入的一个大向量映射到一个神经输出的网格中,在其中,每个输出都是一个聚类。相邻的神经元表示同样的聚类。
神经网络迎来信念网络
玻尔兹曼机器就是类似神经网络的网络,并有着和感知器(Perceptrons)非常相似的单元,但该机器并不是根据输入和权重来计算输出,在给定相连单元值和权重的情况下,网络中的每个单元都能计算出自身概率,取得值为 1 或 0。 因此,这些单元都是随机的 —— 它们依循的是概率分布而非一种已知的决定性方式。 玻尔兹曼部分和概率分布有关,它需要考虑系统中粒子的状态,这些状态本身基于粒子的能量和系统本身的热力学温度。 这一分布不仅决定了玻尔兹曼机器的数学方法,也决定了其推理方法 —— 网络中的单元本身拥有能量和状况,学习是由最小化系统能量和热力学直接刺激完成的。 虽然不太直观,但这种基于能量的推理演绎实际上恰是一种基于能量的模型实例,并能够适用于基于能量的学习理论框架,而很多学习算法都能用这样的框架进行表述。

一个简单的信念网络
一个简单的信念,或者说贝叶斯网络 —— 玻尔兹曼机器基本上就是如此,但有着非直接 / 对称联系和可训练式权重,能够学习特定模式下的概率。
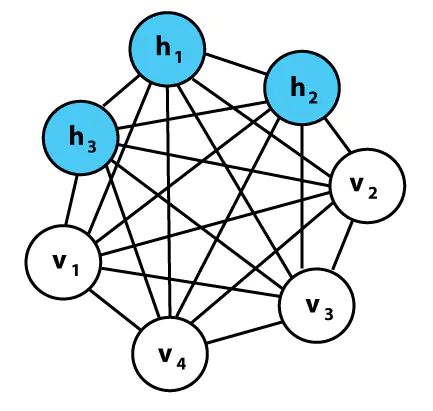
玻尔兹曼机器实例

An explanation of belief nets
90 年代的兴衰 —— 强化学习与递归神经网络 (2000s-2010s)
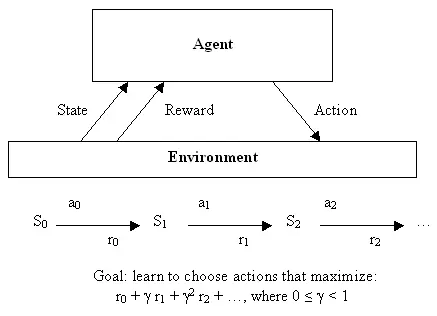
强化学习
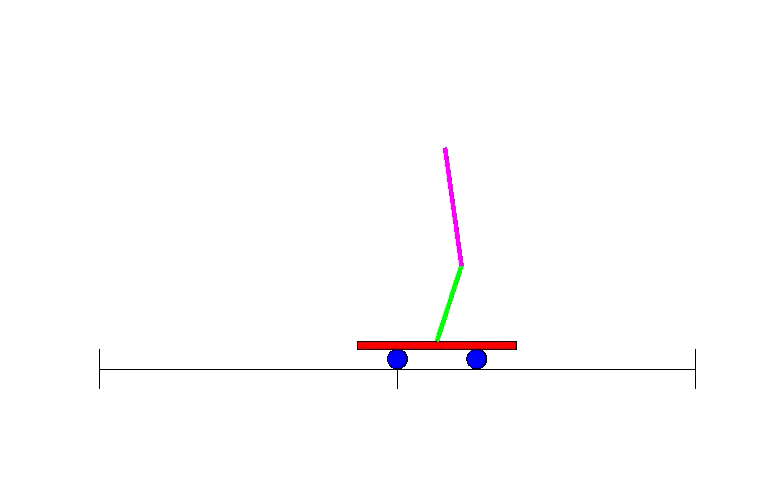
双摆控制问题
双摆控制问题 —— 单摆问题进阶版本,是一个经典的控制和强化学习任务。
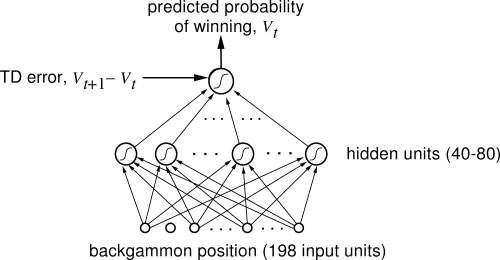
西洋双陆棋游戏中,掌握专家级别水平的神经网络
神经网络变得呆头呆脑
要解决理解语音的问题,研究人员试图修改神经网络来处理一系列输入(就像语音中的那样)而不是批量输入(像图片中那样)。
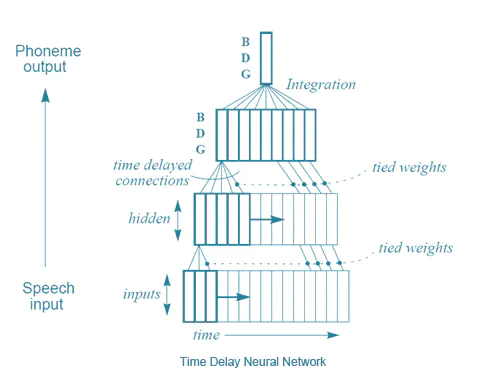
时延神经网络
将神经元回路接回神经网络,赋予神经网络记忆就被优雅地解决了。
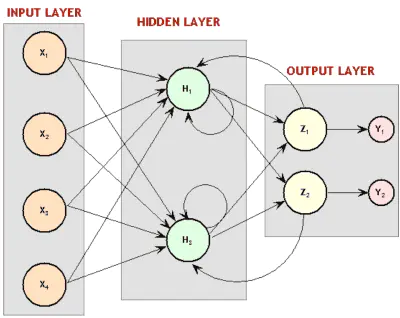
递归神经网络图。还记得之前的玻尔兹曼机吗?大吃一惊吧!那些是递归性神经网络。
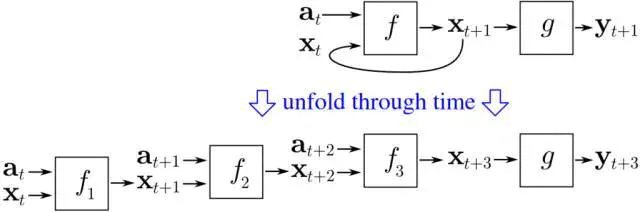
通过时间概念反向传播的直观图解
新的冬日黎明
用它们来工作是十分麻烦的 —— 电脑不够快、算法不够聪明,人们不开心。
深度学习终迎伟大复兴
试问机器学习领域的任何一人,是什么让神经网络研究进行下来,对方很可能提及这几个名字中的一个或全部:Geoffrey Hinton,加拿大同事 Yoshua Bengio 以及脸书和纽约大学的 Yann LeCun。
深度学习的密谋
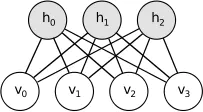
受限的玻尔兹曼机器
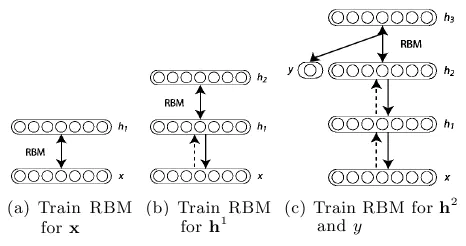
Hinton 引入的层式预训练
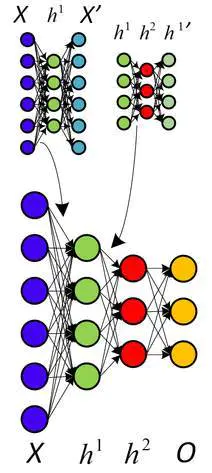
关于非监督式预训练的另一种看法,利用自动代码取代 RBM
蛮力的重要性
大型训练数据集与快速腭化计算的蛮力方法是一个关键。

谷歌最著名的神经网络学习猫。这是输入到一个神经元中最佳的一张
深度学习的上升
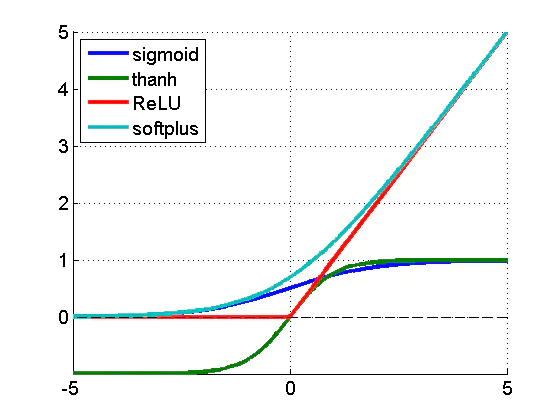
不同的激活函数。ReLU 是修正线性单元
深度学习 = 许多训练数据 + 并行计算 + 规模化、灵巧的的算法
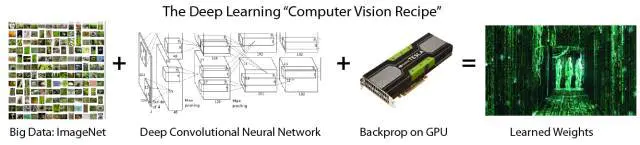
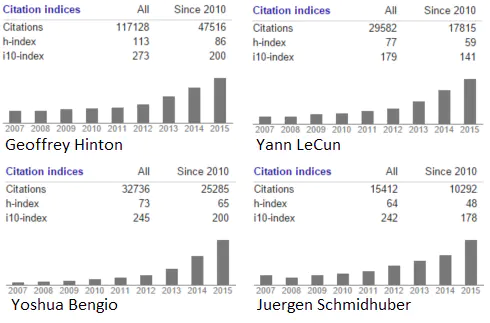
后记:现状
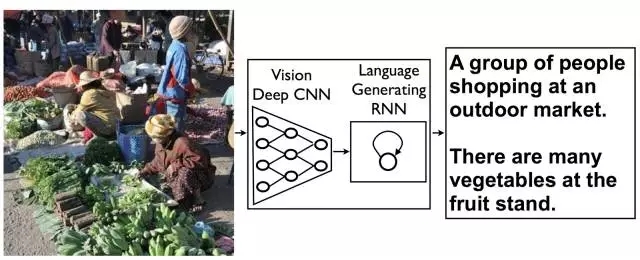
LTSM RNNs 的死灰复燃以及分布式表征的代表
参考
- [1] 深度|神经网络和深度学习简史(第一部分):从感知机到 BP 算法

- [2] 深度|神经网络和深度学习简史(第二部分):BP 算法之后的又一突破 —— 信念网络

- [3] 深度|神经网络和深度学习简史(第三部分):90 年代的兴衰 —— 强化学习与递归神经网络

- [4] 深度|神经网络和深度学习简史(第四部分):深度学习终迎伟大复兴

- [5] http://www.360doc.com/content/17/1207/08/1609415_710706921.shtml
- [6] https://www.skynettoday.com/overviews/neural-net-history
- [7] https://www.andreykurenkov.com/writing/life/lessons-learned-from-failures/
2022-04-23
从 记录 DeepLearning 学习过程 看到两篇非常好的文章。
Thinking
- 周志华:关于机器学习的一点思考
 (周老师的观点客观诚恳~)
(周老师的观点客观诚恳~) - 你知道为什么说深度学习是这时代的炼金术吗?

参考资料快照
- https://www.bilibili.com/video/BV1qf4y1x7kB/
- https://mp.weixin.qq.com/s/_lnyIzWDjzwkyBEjQ1gjtA
- https://www.jianshu.com/p/f90d923b73b5
- https://www.jianshu.com/p/9dc4c2320732
- https://www.jianshu.com/p/5db8170d4bcb
- https://www.jianshu.com/p/e1bac195f06d
- http://www.360doc.com/content/17/1207/08/1609415_710706921.shtml
- https://www.skynettoday.com/overviews/neural-net-history
- https://www.andreykurenkov.com/writing/life/lessons-learned-from-failures/
- https://github.com/xiaoweiChen/DeepLearning-Notes
- http://www.ruanyifeng.com/blog/2017/07/neural-network.html
- http://www.ruanyifeng.com/blog/2016/07/edge-recognition.html
- https://mp.weixin.qq.com/s/sEZM_o5D6AhyMgvocbsFhw
- https://mp.weixin.qq.com/s/y3KqZi68uoWnW_VHV-dtTg
- 机器学习 -- 大型语言模型简史:从 Transformers (2017) 到 DeepSeek-R1(2025) | 20 Feb 2025
- 机器学习 -- DALL·E 2 & 扩散模型 | 21 Dec 2024
- 机器学习 -- 学术论文解读系列(进行中) | 04 Oct 2024
- 机器学习 -- 经典论文 ViT (Vision Transformer) | 24 Jul 2024
- 机器学习 -- 跟李沐学 AI【论文精读】(进行中) | 09 Jul 2024
- 机器学习 -- Attention is all you need | 30 Jun 2024
- 机器学习笔记 -- 3Blue1Brown 深度学习 Deep Learning(已完成) | 29 Jun 2024
- 机器学习 -- 李宏毅 2021/2022 春机器学习课程(进行中) | 31 Aug 2023
- 机器学习 -- 实用机器学习 李沐(进行中) | 31 Aug 2023
- 机器学习 -- ChatGPT Prompt 提示词 吴恩达(进行中) | 28 Jul 2023
- 机器学习 -- 浙江大学 · 机器学习(已完成) | 12 Feb 2023
- 机器学习 -- 人工智能学习路线(进行中……) | 10 Feb 2023
- 机器学习 -- 北交 / 图像处理与机器学习(已完成) | 03 Dec 2022
- 机器学习笔记 -- 人工智能 机器学习 算法概览(已完成) | 13 Oct 2022
- 机器学习笔记 -- 神经网络内部发生了什么?深度学习可视化 | 13 Oct 2022
- 机器学习 -- 吴恩达机器学习 Review(已完成) | 31 Aug 2022
- 机器学习 -- 吴恩达深度学习(进行中) | 31 Aug 2022
- 机器学习 -- 吴恩达机器学习(已完成) | 31 Aug 2022
- 机器学习笔记 -- 神经网络和深度学习简史 | 26 Dec 2020
 .
.