MATHEMATICS --《概率论与数理统计》宋浩老师（已完成）

Posted on March 22, 2024 (珠海)
数学

机器学习的数学基础三部曲的最后一个：高等数学、线性代数、概率论与数理统计，加油。

概率论重新翻看了一遍，机器学习数学基础三部曲终于完成了。感觉概率论讲了三个事情：

已知概率分布，推结论；

根据抽样，反推概率分布；

假设检验，评估推出来的概率分布是否准确。

区间估计：参数未知，用统计量估计未知的参数。

假设检验：参数已知（假设已知），利用统计量检验已知的参数是否靠谱。

这 4 部分数学知识的作用分别是：

概率统计是利用数据发现规律、推测未知的思想方法。
线性代数是利用空间投射和表征数据的基本工具。
微积分与最优化是机器学习模型中最终解决方案的落地手段。
概率图和随机过程是构成机器学习中的核心思想和大量核心应用。

1.1.1 随机试验与随机事件【板书】 24:17

1.1.2 样本空间与事件的集合表示【板书】 11:04

1.1.3 事件间的关系【板书】 1:16:43

1.2.1 概率的初等描述【板书】 02:39

1.2.2 古典概型（排列组合）理论【板书】 32:33

1.2.2 古典概型（排列组合）例题【板书】 45:50

1.2.3 几何概型【板书】 32:21

1.2.4 频率与概率【板书】 11:00

完成。

1.2.5 公理化（理论）【板书】 32:35

完成。

1.2.5 公理化（例题）【板书】 30:23

完成。

1.3.1 条件概率【板书】 20:52

\[P(A \mid B)=\frac{P(A B)}{P(B)}\]

1.3.2 乘法公式【板书】 38:58

\[P(AB)=P(B|A)P(A)\]

1.4.1 全概率公式【板书】 28:41

\[P(B)=\sum_{i=1}^n P\left(A_i\right) P\left(B \mid A_i\right)\]

1.4.2 贝叶斯公式【板书】 36:29

\[\begin{align} P(A|B)&=\frac{P(AB)}{P(B)}\\ &=\frac{P(B|A)P(A)}{P(B)} \\ &= \frac{P(B|A)P(A)}{\sum P(B|A_i)P(A_i)} \end{align}\]

1.5.1 事件的独立性【板书】 08:41

\[P(A|B)=P(A)\]

1.5.1 事件的独立性 #2【板书】 37:37

\[A \cdot B \text { 独立 } \Leftrightarrow P(A B)=P(A) P(B)\]

1.5.1 事件的独立性 #3 例题【板书】 22:18

1.5.2 伯努利模型【板书】 21:52

二项概率公式： $P_n(k)=C_n^k p^k(1-p)^{n-k}=C_n^k p^k q^{n-k}$ $q=1-p$

2.1 随机变量的概念【板书】 13:01

2.2.1 离散型随机变量及其概率分布【板书】 21:05

2.2.2 连续性随机变量及其概率密度函数【板书】 1:06:50

概率为 0 的事件未必不可能事件。
概率为 1 的事件未必是必然事件。

2.2.2 分布函数的定义【板书】 23:56

2.2.2 离散型的分布函数【板书】 39:56

2.2.2 连续型的分布函数【板书】 24:17

2.2.3 0-1 分布【板书】 04:41

2.2.3 几何分布【板书】 04:26

2.2.3 二项分布【板书】 21:37

\[p(X=k)=C_{n}^{k}p^{k}(1-p)^{n-k},k=0,1,2,...n\]

2.2.3 泊松分布【板书】 28:37

\[\frac{\lambda^{k}}{k!}e^{-\lambda},k=0,1,2....\]

2.2.3 超几何分布【板书】 24:38

\[P(X=k)=\frac{C_{M}^{k}C_{n-k}^{N-M}}{C_{n}^{k}},k=0,1,2,....\]

二项分布，$n>=100$，$np<=10$，那个泊松分布近似计算 $\lambda=np$。
超几何分布，N 大，n/N 小，近似为二项分布，近似泊松分布。

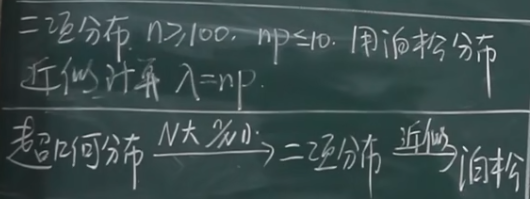
2.2.3 均匀分布【板书】 20:26

2.2.3 指数分布【板书】 24:25

2.2.3 正态分布【板书】 1:10:54

$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} \quad(\mu \in R, \sigma>0)$ 则称 X 服从参数为 $(\mu,\sigma^2)$ 的正态分布（normal distribution），记为 $X-N(μ,σ^2)$

通过新的变量 $z=\frac{x-u}{\sigma}$ 替换原有的变量 $x$ ，这样就完成了 $x\sim N(u,\sigma^2)$ 到 $z\sim N(0,1)$ 标准化。

2.3.1 随机变量函数的分布（离散型）【板书】 10:22

2.3.2 随机变量函数的分布（连续型）【板书】 1:12:36

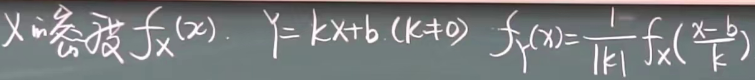
3.1.1 二维随机变量及其分布函数【板书】 34:21

3.1.2 二维离散型的联合分布和边缘分布【板书】 24:50

3.1.3 二维连续型的联合分布与边缘分布 1【板书】 35:00

3.1.3 二维连续型随机变量的边缘密度函数【板书】 32:01

3.2.1 条件分布的定义【板书】 14:32

3.2.2 离散型随机变量的条件分布【板书】 07:28

3.2.3 连续型随机变量的条件分布【板书】 25:25

3.2.4 随机变量的独立性【板书】 26:18

3.3.1 二维离散型随机变量函数的分布【板书】 12:46

泊松分布具有可加性。

3.3.2 二维连续型随机变量函数的分布 1:06:27

卷积公式。

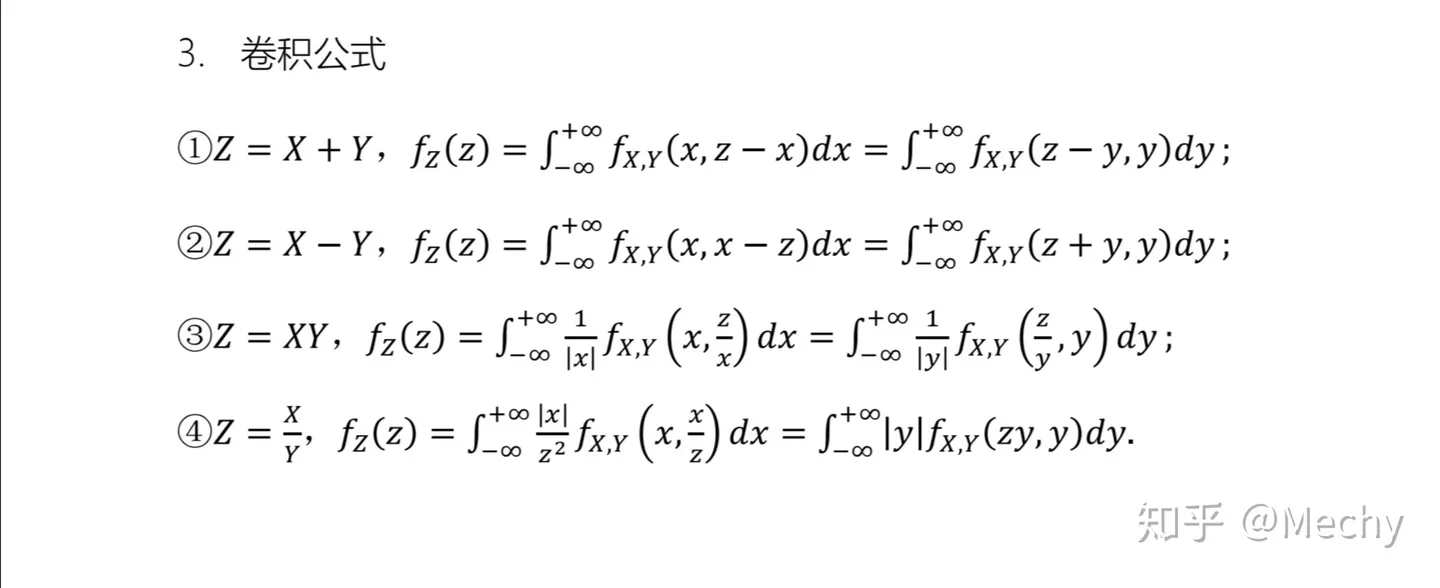
宋浩老师与韩帅的午餐之旅 07:19

4.1.1 离散型变量的数学期望 12:55

\[\begin{array}{l} 定义：\\ X 的分布律：P[X=x_{k}]=p_{k},k=1,2,...\\ X 的概率密度函数：f(x)\\ 随机变量 X 的期望 / 均值：\\ \mathbb{E}(X)=\sum_{k=1}^{\infty }x_{k}p_{k}\\ \mathbb{E}(X)=\int_{-\infty}^{\infty}xf(x)dx \\ 性质：\\ C 为常数 \\ \mathbb{E}(C)=C\\ \mathbb{E}(CX)=C\mathbb{E}(X)\\ \mathbb{E}(X+Y)=\mathbb{E}(X)+\mathbb{E}(Y)\\ X,Y 相互独立 \\ \mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y) \end{array}\]

4.1.2 连续型变量的数学期望 10:12

4.1.3 随机变量函数的数学期望 48:16

4.1.4 数学期望的性质 44:33

4.1.5 条件期望 08:23

4.2.1 方差的定义 16:03

偏离程度。 $\text { 方差 : } D(X) = E(X^2) − E(X)^2$

\[\begin{array}{l} 度量随机变量 X 与其均值 E(X) 的偏离程度 \\ E[\left | X-E(X) \right | ]\\ {\color{Red} 定义：} \\ 方差：D(X)=Var(X)=E([X-E(X)]^2)\\ 标准差：\sigma (X)=\sqrt{D(X)}\\ D(X)=E(X^2)-[E(X)]^2\\ {\color{Red} 性质：}\\ C 是常数 \\ D(C)=0\\ D(CX)=C^2D(X)\\ D(C+X)=D(X)\\ D(X+Y)=D(X)+D(Y)+2E[(X-E(X)(Y-E(Y)]\\ 若 X,Y 相互独立 \\ D(X+Y)=D(X)+D(Y)\\ {\color{Red} 标准化：}\\ 设 E(X)=\mu,D(X)=\sigma^2\\ 定义：X^*=\frac{X-\mu}{\sigma}\Longrightarrow E(X^*)=0，D(X^*)=1\\ \end{array}\]

4.2.2 方差的性质 16:41

4.3.1 常见离散型的期望与方差 39:04

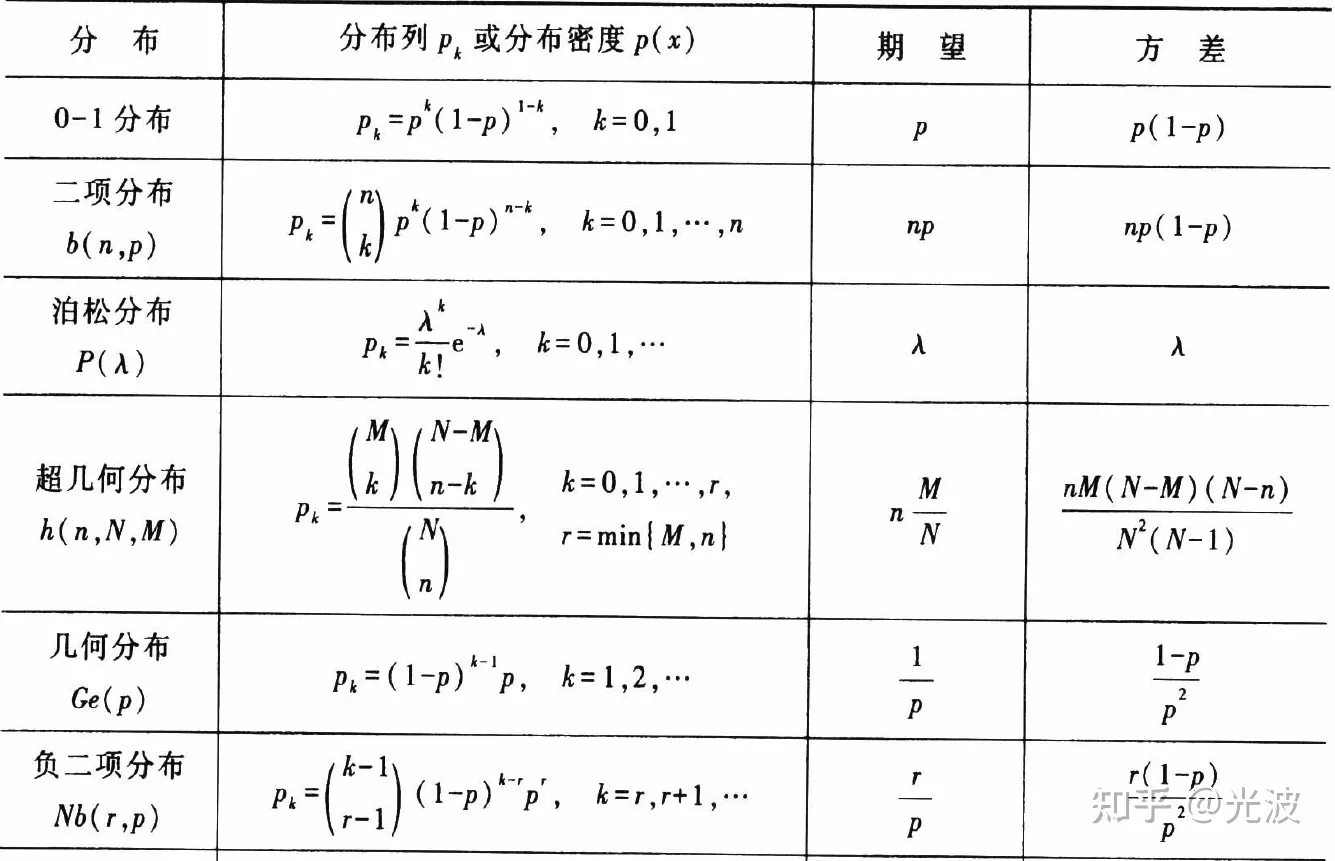
概率论六大分布：

（离散）0-1、二项、泊松
（连续）均匀、指数、正态

数理统计三大分布：

卡方分布、t 分布、F 分布

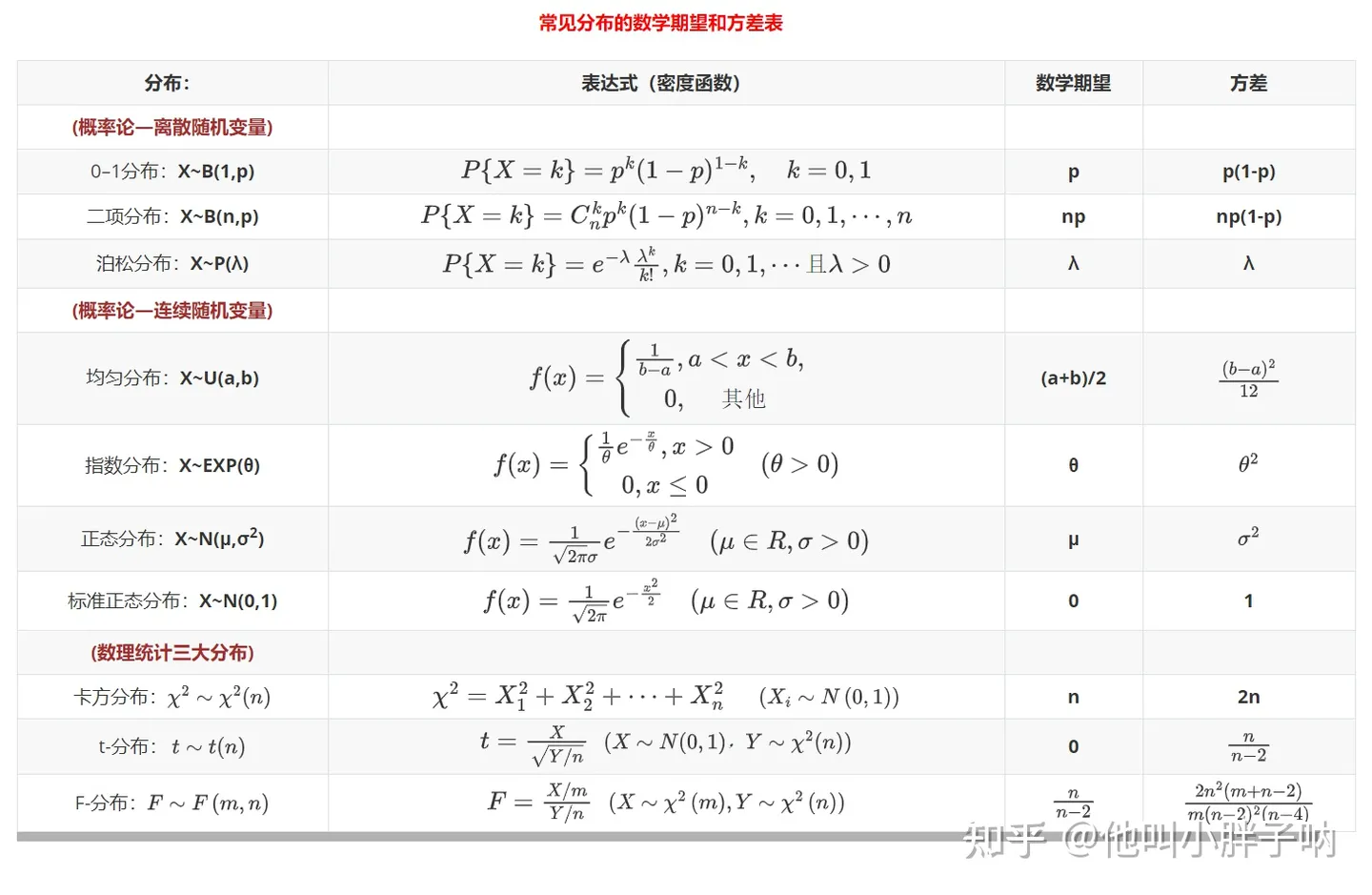
这集很有意思，每个分布的推导过程。

0-1。例如硬币投掷（正面或反面）、产品合格或不合格的检验等等。
二项。在二项分布中，每次试验有两种可能的结果，通常用 0 和 1 来表示（或者用其他两个互斥的值）。
几何。几何分布描述了在多次试验中首次成功所需要的试验次数的概率分布。
泊松。例如自然灾害的发生次数、客户到达商店的次数、电子邮件到达某个邮箱的次数等等。

4.3.2 常见连续型的期望与方差 26:13

这一段很有意思，反复套娃，老师讲着讲着突然来了句，“我讲的，都是些什么玩意？！”

【coindance】抖肩舞–宋老师友情出演 02:27

4.4.1 协方差 27:18

$D(X \pm Y)=D X+D Y \pm 2 \operatorname{Cov}(X . Y)$ $\operatorname{Cov}(X . Y)=E(X Y)-EXEY$

独立时，协方差一定等于零。协方差等于零不一定独立。因为有特殊情况。

特征工程里面消量纲。

\[\begin{array}{l} 定义 :\\ 协方差：Cov(X,Y)=E[(X-E(X)(Y-E(Y))]\\ 性质：\\ Cov(X,Y)=Cov(Y,X)\\ Cov(X,X)=D(X)\\ Cov(X,Y)=E(XY)-E(X)E(Y)\\ Cov(aX,bY)=abCov(X,Y)\\ Cov(X_{1}+X_{2},Y)=Cov(X_{1},Y)+Cov(X_{2},Y)\\ 标准化：\\ 相关系数（线性）：\rho _{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)} }\\ \left |\rho _{XY} \right |\le 1\\ \left |\rho _{XY} \right | 大 \Longrightarrow X,Y 线性相关程度好；\\ \rho _{XY}=0\Longrightarrow X,Y 线性不相关 \\ \end{array}\]

协方差矩阵

\[\begin{array}{l} 2 个随机变量 X_{1},X_{2}：\\ 协方差矩阵 \Sigma =\begin{Bmatrix} Cov(X_{1},X_{1}) & {\color{Red} Cov(X_{1},X_{2})} \\ {\color{Red} Cov(X_{2},X_{1})} & Cov(X_{2},X_{2}) \end{Bmatrix}\\ =\begin{Bmatrix} \sigma_{1}^2 & \sigma_{12}\\ \sigma_{21}& \sigma_{2}^2 \end{Bmatrix}\\ 3 个随机变量 X_{1},X_{2},X_{3}：\\ 协方差矩阵 \Sigma =\begin{Bmatrix} \sigma_{1}^2& \sigma_{12}& \sigma_{13}\\ \sigma_{21}& \sigma_{2}^2& \sigma_{23}\\ \sigma_{31}& \sigma_{32}& \sigma_{3}^2 \end{Bmatrix} \end{array}\]

4.4.2 相关系数 40:32

\[\rho=\frac{\operatorname{cov}(X, Y)}{\sqrt{D X} \sqrt{D Y}}=\frac{E(X Y)-E X E Y}{\sqrt{D X} \sqrt{D Y}}\]

4.5 中心矩与原点矩 05:11

5.1 大数定律 1:06:03

玄甲青梅竹马朝露春水桃花蛾眉朱雀黄桐蚍蜉金缕太阿

5.2 中心极限定理 46:12

二项分布。

n 大，np 适中。看成泊松分布。
n 大，np 大。看成正态分布。

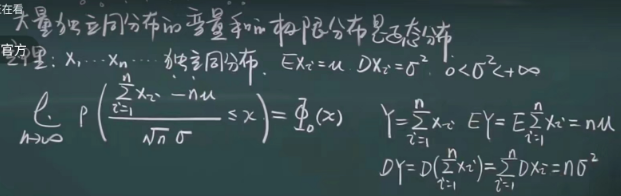
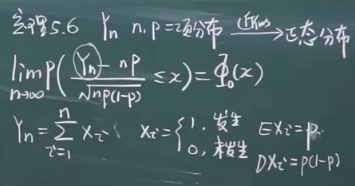
6.1 总体与样本 10:57

6.2.1 统计量的定义 06:25

6.2.2 常用统计量 23:24

6.3.1 抽样分布 1:10:12

卡方分布

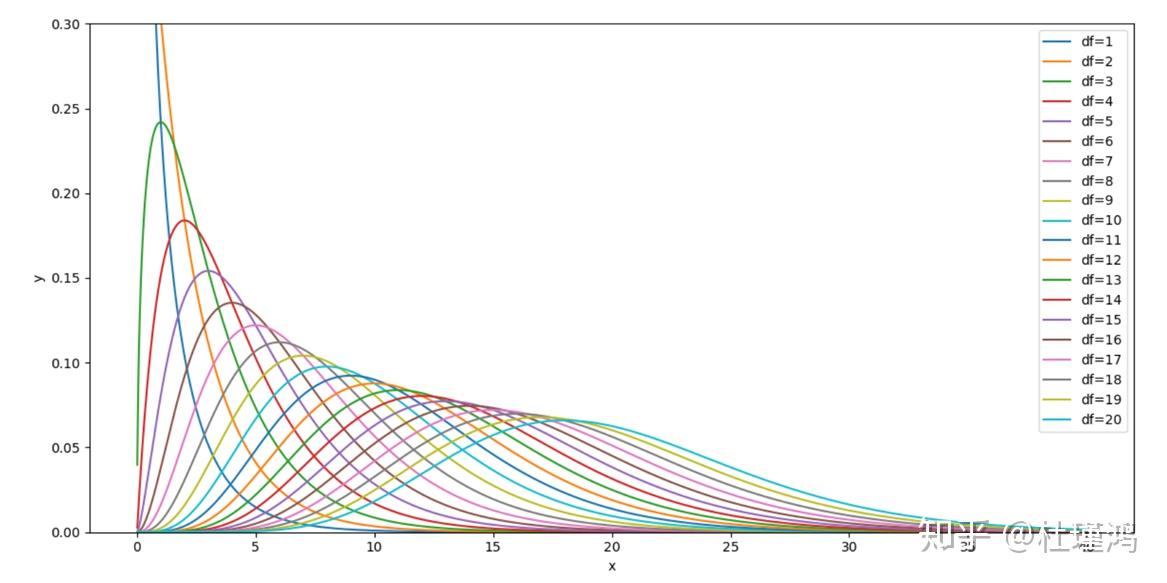
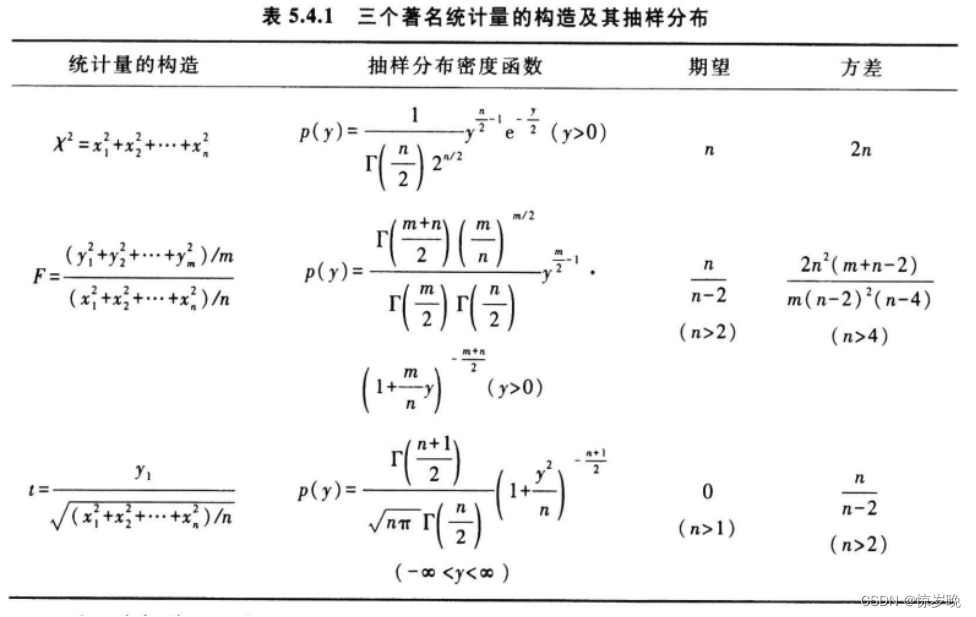
$\chi^{2}$ 分布是由 $n$ 个相互独立的标准正态分布的平方和确定的分布，记作 $\chi^2\sim\chi^2(n)$，即 $\chi^{2}\:=\:\sum_{i}^{n}\:(\:N(0,1)\:)_{i}^{2}\:\sim\chi^{2}\:(n)$。

$t$ 分布的分子是一个 $N(0,1)$，分母是自由度为 $n$ 的 $\chi^{2}$ 分布与自由度 $n$ 的比值再开方确定的分布，记作 $t\:\sim\:t\left(n\right)$，即 $t\:=\:\frac{N\left(0,1\right)}{\sqrt{\chi^{2}\left(n\right)/n}}\:\sim\:t\left(n\right)$。

$F$ 分布是由两个 $\chi^{2}$ 分布与其自由度比值的比值确定的分布，记作 $F\sim F(n_1,n)$。

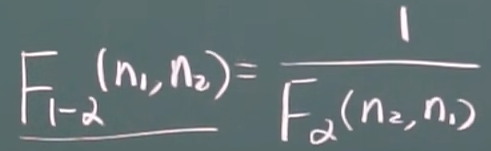
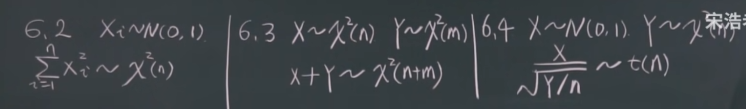
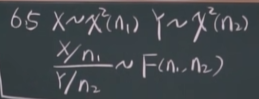
宋浩劝学 宋浩老师讲了一段，我们为什么要努力？生活是现实，不是童话，主要是让家人更体面一点，更舒服一点。

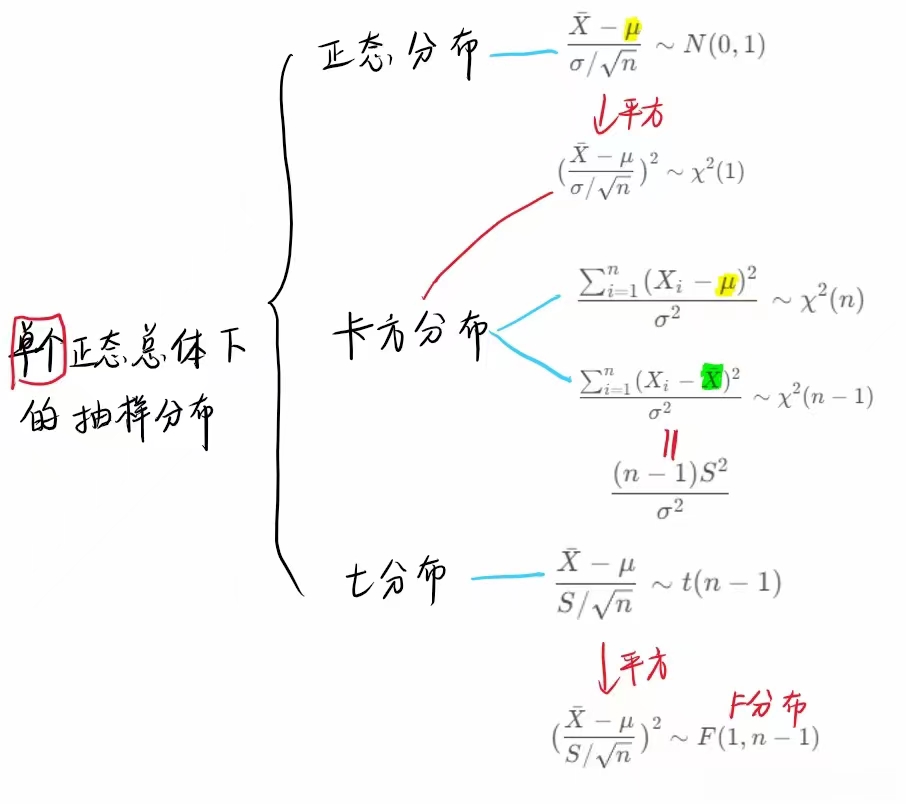
6.3.2 正态总体下的抽样分布 45:32

7.1.1 参数估计 · 矩估计法 38:30

7.1.2 参数估计 · 极大似然估计 59:26

总体的概率（离散）/ 密度（连续）函数。
写似然函数 $L(\lambda)$，参数是 $\lambda$。
两边取的 ln $\ln L(\lambda)$
对 $\lambda$ 求导，令导数 $=0$。

7.2 点估计的优良性准则 30:44

无偏性、有效性、一致性。

求期望： $\text { 无偏性 } E \hat{\theta}=\theta$

求方差： $\text { 有效性 } D\left(\hat{\theta}_1\right) \leq D\left(\hat{\theta}_2\right)$

求极限： $\lim _{n \rightarrow+\infty} P(|\hat{\theta}-\theta|<\varepsilon)=1$

财富 radio 宋浩：数学有意思【精华版】 03:58

7.3.1 置信区间与枢轴变量的定义 31:24

枢轴

机关运转的中轴。比喻中央权力机关或相位。
喻中枢，中心。

7.3.2 一个正态总体的期望和方差的区间估计 40:11

8.1【1】假设检验问题 36:14

这个不好，后面的姜老师黑板书版本更好。

8.1【2】假设检验的基本概念 09:46

8.1【3】假设检验的基本思想 24:40

8.1【4】两类错误 11:25

8.2【1】均值的假设检验 1:04:41

\[U=\frac{\bar{x}-\mu_0}{\sigma_0 / \sqrt{n}} \sim N(0,1)\] \[T=\frac{\bar{X}-\mu_0}{S / \sqrt{n}} \sim t(n-1)\]

8.2【2】方差的假设检验 40:06

8.3【1】均值的差异性检验 42:55

8.3【2】方差的差异性检验 47:13

山东教育电视台–宋浩老师 00:26

8.1 【姜老师】假设检验的基本概念 1 45:45

这个是黑板板书版本。

8.1 【姜老师】假设检验的基本概念 2 48:17

8.2 【姜老师】一个正态总体的参数假设检验（1） 1:18:45

8.2 【姜老师】一个正态总体的参数假设检验（2） 37:58

8.3【姜老师】两个正态总体的参数假设检验 1:23:01

区间估计：参数未知，用统计量估计未知的参数。
假设检验：参数已知（假设已知），利用统计量检验已知的参数是否靠谱。

【以下旧版 PPT】

1.1 随机事件 1:00:07
1.2 （0）排列组合的补充知识 52:01
1.2 古典概型 23:33
1.2 几何概率模型 32:31
1.2 公理化定义 32:40
1.3 条件概率 15:23
1.3 乘法公式 35:16
1.4 全概率公式 28:00
1.4 贝叶斯公式 38:36
1.5 独立性 1:12:05
1.5 伯努利概型 28:09
2.1 随机变量的概念 14:01
2.3.1 常见离散型变量的分布 1:26:12
2.3.1 超几何分布 17:27
2.3.2 均匀分布指数分布 30:08
2.3.2 正态分布 1:02:23
2.4.1 离散变量函数的分布 12:16
2.4.2 连续函数变量函数的分布 OK 35:19
3.1.1 二维随机变量及其分布函数 17:53
3.1.2 二维离散型的联合概率分布和边缘概率分布 22:17
3.1.3 二维连续型的联合概率密度及其边缘概率密度 1:15:26
3.2.1 条件分布的概念 16:13
3.2.2 离散型的条件概率分布 17:47
3.2.3 连续型的条件分布 43:57
3.2.4 随机变量的独立性 25:19
3.3.1 二维离散型随机变量函数的分布 12:21
3.3.2 二维连续型随机变量函数的分布 44:47
4.1.1 离散型随机变量的数学期望 05:51
4.1.2 连续型变量的数学期望 12:12
4.1.3 随机变量函数的期望 20:32
4.1.4 数学期望的性质 18:18
4.1.5 条件数学期望 07:02
4.2.1 方差的概念 26:18
4.2.2 方差的性质 19:29
4.3.1 常见离散型分布的数学期望和方差 16:29
4.3.2 常见连续型的期望和方差 16:45
4.4.1 协方差 24:38
4.4.2 相关系数 30:00
4.5 随机变量的矩 14:11
5.1 大数定律 42:28
5.2 中心极限定理 39:59
6.1 总体与样本 11:09
6.2 统计量 27:33
6.3.1 重要分布 36:01
6.3.2 正态总体下的抽样分布 17:26
7.1.1 矩估计法 40:04
7.1.2 极大似然估计法 25:47
7.2 点估计优良性准则 40:15
7.3.1 置信区间的概念 13:55
7.3.2 一个正态总体参数的区间估计 32:37
7.3.3 两个正态总体参数的区间估计 10:21
【1】加法原理乘法原理 08:39
【2】排列 17:57
【3】组合 16:47

参考资料快照

机器学习的数学基础系列文章

MATHEMATICS -- 生成模型数学 —— 概率论基础 | 27 Sep 2024
MATHEMATICS --《线性代数》奇异值分解（SVD） | 04 Apr 2024
MATHEMATICS --《概率论与数理统计》宋浩老师（已完成） | 22 Mar 2024
MATHEMATICS -- 难懂的数学（已完成） | 10 Sep 2022
MATHEMATICS --《线性代数》宋浩老师（已完成） | 23 Aug 2022
MATHEMATICS --《高等数学》同济版宋浩老师（已完成） | 13 Aug 2022
机器学习笔记 -- 环境搭建 & 数学基础 | 29 Aug 2020