MATHEMATICS --《线性代数》奇异值分解（SVD）

Posted on April 4, 2024 (珠海)
数学

奇异值分解本质上是 特征值分解的一个扩展 ，就是将一个 $m \times n$ 的矩阵分解成三个矩阵相乘。

矩阵分解动画讲解，其实也很简单！ https://www.bilibili.com/video/BV1zqYpzwEaQ/
代数明珠–奇异值分解（SVD）生动动画演示！ https://www.bilibili.com/video/BV1n5YyztEVk/
用可视化看懂 SVD 奇异值分解 https://www.bilibili.com/video/BV1Rrp3zYE3i/

特征值分解

特征值和特征向量

\[Av=\lambda v\]

其中 A 是一个 n 维的方阵，v 是 n 维特征向量，$\lambda$ 是个数字（特征值）。每一个特征值都对应一个特征向量。

上面式子也可以理解为：A 为对 v 向量的变换矩阵，由于 $\lambda$ 仅仅是一个数值，所以这个变换 只有拉伸没有旋转 。

特征值分解

如果方阵 A 的秩为 m，那么就有 m 个特征值，也对应 m 个特征向量（正交）。每一个都满足表达式 $Av=\lambda v$。那么，就可以写成如下形式

\[AV=V\zeta\]

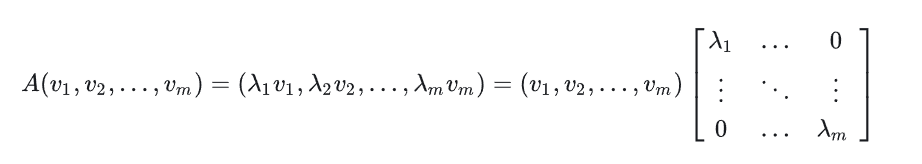
V 是特征向量组成的矩阵，$\zeta$ 是对角线上元素为特征值的的对角阵。方程两边同时乘以 V 矩阵的逆得到：

\[A=V\zeta V^{-1}\]

如果矩阵 A 不是方阵，那么就用到了奇异值分解。

奇异值分解

定义

\[A=U\Sigma V^{-1}\]

A 是将要分解的大小为 $m \times n$ 的矩阵。U 是 m 维的方阵。V 是 n 维的方阵。 $\Sigma$ 是除主对角线元素以外全为 0 的矩阵，大小为 $m \times n$。示意图如下：

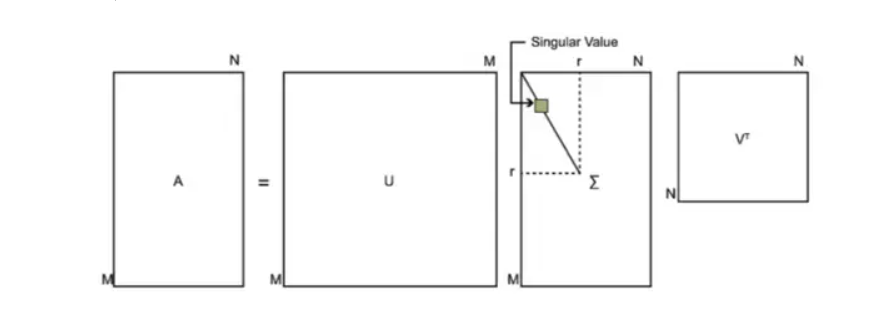
求解

还是按照特征值求解的思路，现在的矩阵 A 不是方阵，如果将其乘以自己的转置矩阵就变成了方阵，是方阵就可以求其特征值和特征向量。

$\Sigma$ 主对角线上的元素就是矩阵对应的奇异值，按从大到小的顺序排列，奇异值越大代表其对应的特征向量包含的特征越多。利用这一点，可以对数据进行降维，压缩等应用。

奇异值分解代表的物理意义

一个矩阵可以理解为一个线性变换，如果矩阵是对角阵，那么对应的变换是拉伸。如果矩阵是由正交向量组成的，那么对应的变换是旋转。所以，奇异值分解就是将一个线性变换分解成先旋转，后拉伸，最后再旋转的一个过程。

为什么一般的线性变换不能只用“拉伸”（对角矩阵）来表示，而一定要引入“旋转”？

为什么一般的线性变换不能只用“拉伸”（对角矩阵）来表示，而一定要引入“旋转”？

从几何自由度和线性代数结构两条线解释。

1️⃣ “直接拉伸”在数学上意味着什么？

“只拉伸、不旋转”对应的矩阵形式是：

\[A = D\]

其中 $D$ 是一个对角矩阵：

\[D = \begin{pmatrix} \lambda_1 & 0 & \cdots \\ 0 & \lambda_2 & \cdots \\ \vdots & & \ddots \end{pmatrix}\]

几何意义是：

沿着固定的坐标轴方向
分别缩放（拉伸/压缩）

👉 关键限制： 拉伸方向必须是当前坐标轴方向，而且彼此正交

2️⃣ 但一般的线性变换“拉伸方向”并不对齐坐标轴

现实中的线性变换 $A$ 往往：

把一个方向映射到斜着的方向
拉伸方向不是原坐标轴
不同方向之间还可能发生“混合”

举个 2D 的例子：

\[A = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}\]

这是一个剪切（shear）变换：

x 方向会“带着 y 一起跑”
没有任何坐标轴方向是“纯拉伸”的

👉 你找不到一个坐标系，能让它在原坐标下表现为“只拉伸”

3️⃣ SVD 的关键洞察：

👉 “那我先换一套正交坐标系不就行了？”

这正是 SVD 的本质。

\[A = U \Sigma V^\top\]

几何解释：

$V^\top$：把输入空间旋转到一个“合适的坐标系”
$\Sigma$：在这个新坐标系中 纯拉伸
$U$：再把结果旋转到输出空间

👉 核心点：

不是不能拉伸，而是要在“对的方向”上拉伸

4️⃣ 为什么“两个旋转 + 一个拉伸”是最省事的？

这是一个自由度匹配的问题。

在 n 维空间中：

一般线性变换： 👉 $n^2$ 个自由度
对角矩阵（纯拉伸）： 👉 只有 $n$ 个自由度
正交矩阵（旋转）： 👉 $n(n-1)/2$ 个自由度

\[n + 2 \cdot \frac{n(n-1)}{2} = n^2\]

👉 刚好补齐所有自由度

所以：

“只拉伸”不够表达力
“拉伸 + 两次旋转”刚好能表达所有线性变换

5️⃣ 直觉版总结一句话

一般线性变换不是“沿坐标轴拉伸”，而是“沿某些斜着的正交方向拉伸”。

SVD 的旋转只是帮你把坐标轴转到这些“真正的拉伸方向”上。

6️⃣ 一句话终极答案

奇异值分解中的旋转并不是多余的，它们用于将线性变换对角化到合适的正交基下；只有在这些特征方向上，线性变换才能表现为纯拉伸。

参考资料快照

机器学习的数学基础系列文章

参考资料快照

本文短链接：
If you have any questions or feedback, please reach out