MATHEMATICS -- 难懂的数学（已完成）

难懂的数学 傅里叶、拉普拉斯、卷积、欧拉方程、梯度散度、拉格朗日方程、奈奎斯特采样、虚数等抽象难懂数学一网打尽。

P1 傅里叶变换、傅立叶级数和频谱 15:46

https://blog.csdn.net/weixin_48524215/article/details/122802096

我们将无限个振幅无限小的正弦波叠加在一起就可以测量叠加后波的频率密度，这就是我们说的波形频谱（Frequency Spectrum）。

傅里叶变换可以看作傅里叶级数的极限形式。 傅里叶级数针对的是周期性函数，傅里叶变换针对的是非周期性函数，它们在本质上都是一种把信号表示成复正选信号的叠加。

2023.09.02 2024.06.05

P2 拉普拉斯变换直观理解 19:56

Fourier 变换时常会遇到的问题就是积分不收敛，当加上那个指数下降的项之后大多情形都解决了。

单边拉普拉斯变换和傅里叶变换的定义如下：

\[\begin{array}{l} F(s)=\int_{0}^{\infty} f(t) \mathrm{e}^{-s t} \mathrm{~d} t \quad \operatorname{Re}[s]>\sigma_{0} \\ F(\mathrm{j} \omega)=\int_{-\infty}^{\infty} f(t) \mathrm{e}^{-\mathrm{j} \omega t} \mathrm{~d} t \end{array} \\\]

没怎么彻底看懂。mark 2023.09.05

听完一头雾水，茅塞更堵了。 2024.06.05

P3 梯度和偏导数 Gradients and Partial Derivatives 05:24

2024.06.05

P4 散度和旋度 Divergence and Curl 25:33

散度 – 空间上 旋度 – 曲面上 2023.09.06 2024.06.05

P5 欧拉-拉格朗日方程 Euler-Lagrange equation explained intuitively - Lagrangian Mechanics 18:23

欧拉-拉格朗日方程（Euler-lagrange equation）：

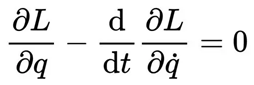
泛函分析，没完全看懂。2023.09.08

花里胡哨的动画，还是没怎么看懂。 2024.06.07

P6 卷积和单位脉冲响应 09:22

P7 特征值和特征向量，虚实 Eigenvalues and Eigenvectors, Imaginary and Real 12:42

P8 点积和叉积的直观解释 04:08

P9 曲率和奇异 Intrinsic Curvature and Singularities 11:37

2024.06.08

P10 积分基础解释 Calculus – The foundation of modern science 19:04

微积分 区域函数拆解与求和的总过程。

This is the foundation allowing us to write equations describing how all objects in the universe behave.

This is the language in which the fundamental laws of the universe are written in.

Mathematics is not the language of the universe. Mathematics is the language we, humans, use to explain the universe.

The universe must have some regularities, some patterns, in order for life to exist. A chaotic universe could not support life.

So, we exist, we must exist in a universe with patterns, regularities, laws. And mathematics is th language we use to describe those laws.

P11 二重积分和极积分 Double integrals and Polar integrals_ Explained with 3D visualizations 16:02

P12 虚数和复数变量直观解释 Imaginary Numbers, Functions of Complex Variables_ 3D animations. 14:33

复数域的函数很难三维表示，这个图突然解开了多年的疑惑，输入是实部虚部的 XY 坐标，输出是长度角度的极坐标，其中角度用颜色表示，图上再取了一个 log。

复数的四种表示形式：

1. 代数形式：$F=a+jb$；
2. 三角形式：$F=|F|(cos(φ)+jsin(φ))$，这里的 $|F|$ 是 $F$ 的模；
3. 指数形式：$F=|F|e^(jφ)$，$jφ$ 是 $e$ 的指数角标；
4. 极坐标形式：$F=|F|∠φ$；

P13 指数爆炸哲学 Exponential Growth and its Philosophical Implications 07:12

完成。

P14 概率-量子与经典 Probability - Quantum and Classical 22:48

这个简单。 2024.06.12

P15 张量协变、逆变、秩直观解释 Tensors Explained Intuitively_ Covariant, Contravariant, Rank 11:44

P16 奈奎斯特采样定理 17:19

P17 欧拉公式 14:31

P18 三维代数学 Algebra and Mathematics. Explained with easy to understand 3D animations. 40:00

P19 四维球体、四面体和立方体的四维旋 Fourth Dimension rotation of 4D spheres, tetrahedrons, and cubes 03:48

P20 绘制第 4、5、6 和 7 维空间 Drawing the 4th, 5th, 6th, and 7th dimension 03:51

完成。

P21 大地测量学之美 09:59

完成。

P22 虚数是真的（1） 05:48

完成。

P23 虚数是真的（2） 05:17

完成。

P24 虚数是真的（3） 04:42

完成。 \(x^3=15 x+4\)

\[\begin{aligned} & x^3=15 x+4 \\ & x=\sqrt[3]{\frac{d}{2}+\sqrt{\frac{d^2}{4}-\frac{c^2}{27}}}+\sqrt[3]{\frac{d}{2}-\sqrt{\frac{d^2}{4}-\frac{c^2}{27}}} \\ & x=\sqrt[3]{\frac{4}{2}+\sqrt{\frac{43}{4}-\frac{16^2}{27}}}+\sqrt[3]{\frac{4}{2}-\sqrt{\frac{4^2}{4}-\frac{15^2}{27}}} \\ & x=\sqrt[3]{2+\sqrt{4-125}}+\sqrt[3]{2-\sqrt{4-125}} \\ & x=\sqrt[3]{2+(\sqrt{-121})}+\sqrt[3]{2 \cdot(\sqrt{-121})} \\ & \end{aligned}\]

而答案就是 4。

P25 虚数是真的（4） 02:57

完成。

P26 虚数是真的（5） 04:38

完成。 虚数是在研究三次方程的通解的过程中被发现的。

P27 虚数是真的（6） 03:39

完成。

P28 三角学直观解释 Trigonometry - Easy to understand 3D animation 16:29

完成。

P29 拉普拉斯方程 05:31

梯度的散度。 可以对应山峰和山谷。 对应函数的最大值或者最小值。 2024.06.20

---

参考资料快照

• https://www.bilibili.com/video/BV1kX4y1u7GJ
• https://blog.csdn.net/weixin_48524215/article/details/122802096