MATHEMATICS --《高等数学》同济版 宋浩老师(已完成)
重新学了一遍《高数》,给宋浩老师冲了 100 块钱。宋浩老师的《高数》累计播放量上亿,是 B 站播放量第一的视频。 每天睡觉前,学习一小时,日拱一卒 功不唐捐,76 小时的视频,看了三个月。
- 《线性代数》
- 《微积分》
- 《概率论与数理统计》
- 《高等数学》
从新学习,并用 mathjax 做笔记。
mathjax
html2text
公式及时编辑
在线函数图像
这 4 部分数学知识的作用分别是:
- 概率统计是利用数据发现规律、推测未知的思想方法。
- 线性代数是利用空间投射和表征数据的基本工具。
- 微积分与最优化是机器学习模型中最终解决方案的落地手段。
- 概率图和随机过程是构成机器学习中的核心思想和大量核心应用。
1.1 映射 47:15
定义域 $D_f$ Domain 值域 $R_f$ Range
实数 $\mathbb{R}$
【口误修正】Rg 包含于 Df 01:04
1.1 函数 12:22
1.1 函数的几种特性 34:20
note $ \exists $ \exists 存在 $ \forall $ \forall 任给(Any)
\forall x \in X, \quad \exists y \leq \epsilon
\(\forall x \in X, \quad \exists y \leq \epsilon\)
from  连加:$\sum$: \sum
连乘:$\prod$: \prod
连加:$\sum$: \sum
连乘:$\prod$: \prod
-
求和符号
\sum显示为 $\sum$ -
\sum_{i=0}^n显示为 $\sum_{i=0}^n$ -
极限符号
\lim显示为 $\lim$ -
\lim_{x\to\infty}显示为 $\lim_{x\to\infty}$ -
\displaystyle\lim_{x\to\infty}显示为 $\displaystyle\lim_{x\to\infty}$ -
连乘
\prod_{i=1}^{n} a_i显示为 $\prod_{i=1}^{n} a_i$
并非每个周期函数都有最小周期
函数 $f(x)$ 满足以下形式: $f(n+T)=f(n)$ 称函数为周期函数。
狄利克雷(Dirichlet)函数
\[D(x)=\left\{ \begin{array}{ll} 1, & x \in Q \\ 0, & x \in Q^C \end{array}\right.\]显然该函数是以任何正有理数 $r$ 为周期的周期函数,所以它没有最小正有理数周期。
1.1 反函数 复合函数 初等函数 18:56
对数运算符 \log \ln \lg
- $\log_{e}{x} = \ln{x}$
- $\log_{10}{x} = \lg{x}$
1.2 数列极限的定义 32:29
对数列 $\{x_n\}$,若存在常数 $a$,对于任意 $ε>0$,总存在正整数 $N$,使得当 $n>N$ 时,$|x_n-a|<ε$ 成立,那么称 $a$ 是数列 $\{x_n\}$ 的极限。
1.2 收敛数列的性质 25:26
唯一性、有界性定义、保号性。
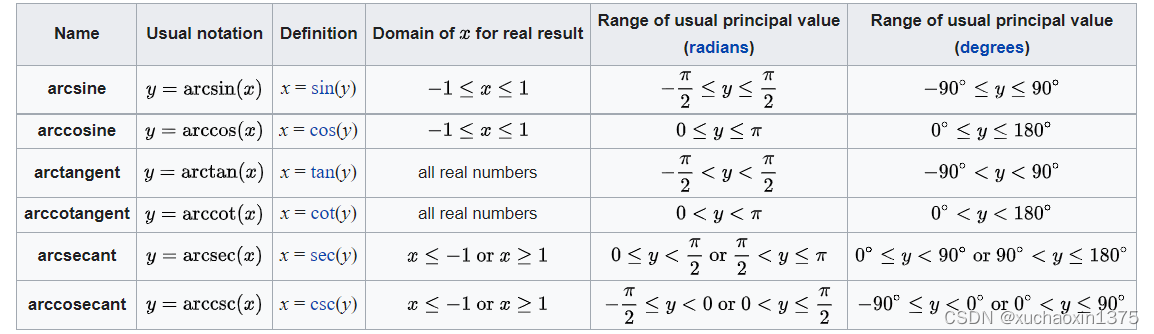
反三角函数介绍 20:23
基本初等函数包括幂函数、指数函数、对数函数、三角函数、反三角函数和常数函数。
1.3 函数极限 1:22:36
设函数 $f(x)$ 在点 $x_0$ 的某一去心邻域内有定义,如果存在常数 $A$,对于任意给定的正数 $\epsilon$ (无论它多么小),总存在正数 $\delta$,使得当 $x$ 满足不等式 $0<|x-x_0|<\delta$ 时,对应的函数值 $f(x)$ 都满足不等式:
\[|f(x)-A|<\epsilon\]那么常数 $A$ 就叫做函数 $f(x)$ 当 $x \to x_0$ 时的极限,记作
\[\lim_{x\to x_0}f(x)=A\]- 函数极限的唯一性
- 局部保序性
- 局部保号性
- 局部有界性
人生到处知何似,应似飞鸿踏雪泥。
泥上偶然留指爪,鸿飞那复计东西。
老僧已死成新塔,坏壁无由见旧题。
往日崎岖还记否,路长人困蹇驴嘶。
1.4 无穷小与无穷大 20:01
note
首先我们要正确认识无穷小,简单来说无穷小就是以 $0$ 为极限的函数。
1.5 极限运算准则(修后)42:04

1.6 极限存在准则 两个重要极限 48:48
- 准则 1:夹逼准则(放缩思想)
- 准则 2:单调有界数列必有极限
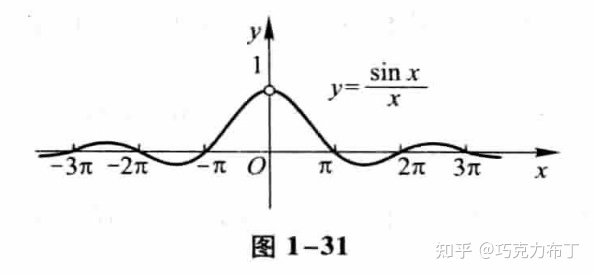
- 重要极限 1:$\lim_{x \rightarrow 0}{\frac{sinx}{x}} = 1$
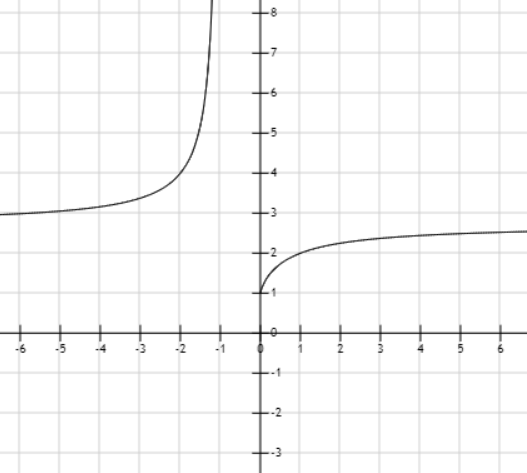
- 重要极限 2:$\lim_{x \rightarrow \infty}{(1+\frac{1}{x})^{x}} = e$
- 柯西极限存在准则
定义:数列 $\{x_n\}$ 收敛 $\Leftrightarrow$ 对于任意给定的正数 $\varepsilon$,存在任意小正整数,使得当 $m>N$,$n>N$ 时,有 \(|x_{n}-x_{m}|<\varepsilon\)
1.7 无穷小的比较 32:59
两个无穷小之比的极限反映了出不同的无穷小趋近于零的“快慢”程度。
知乎
两个无穷小量之间又分为 高阶无穷小,低阶无穷小,同阶无穷小,等价无穷小。
假设在自变量同一个变化过程中,有 $\alpha$,$\beta$ 两个无穷小,且 $\alpha\ne0$,$\lim\frac{\beta}{\alpha}$ 也是这个过程中的极限,有如下定义:
- 高阶的无穷小,记作 $\beta=o(\alpha)$;
- 低阶的无穷小;
- 同阶无穷小;
- $k$ 阶无穷小;
- 等价无穷小,记作 $\alpha \sim \beta$。
- 定理 1:$\beta$ 与 $\alpha$ 是等价无穷小的充分必要条件是 $\beta=\alpha+o(\alpha)$。
- 定理 2:设 $\alpha\sim\alpha'$,$\beta\sim\beta'$,且 $\lim\frac{\beta'}{\alpha'}$ 存在,则 $\lim\frac{\beta}{\alpha}=\lim\frac{\beta'}{\alpha'}$。
- 定理 2 表明,求两个无穷小之比的极限时,分子及分母可用等价无穷小代替,适当选择等价无穷小可简化计算。
等价无穷小的使用条件是:
- 被代换的量在取极限的时候极限值为 0。
- 被代换的量,作为被乘或者被除的元素时可以用等价无穷小代换,但是作为加减的元素时就不可以。
等价无穷小是无穷小之间的一种关系,指的是:在同一自变量的趋向过程中,若两个无穷小之比的极限为 1,则称这两个无穷小是等价的。无穷小等价关系刻画的是两个无穷小趋向于零的速度是相等的。
1.8 函数的连续性与间断点 39:27
积化和差 \({\displaystyle \sin \alpha \cos \beta ={\sin(\alpha +\beta )+\sin(\alpha -\beta ) \over 2}} \\ {\displaystyle \cos \alpha \sin \beta ={\sin(\alpha +\beta )-\sin(\alpha -\beta ) \over 2}} \\ {\displaystyle \cos \alpha \cos \beta ={\cos(\alpha +\beta )+\cos(\alpha -\beta ) \over 2}} \\ {\displaystyle \sin \alpha \sin \beta =-{\cos(\alpha +\beta )-\cos(\alpha -\beta ) \over 2}} \\\)
和差化积 \({\displaystyle \sin \alpha +\sin \beta =2\sin {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}} \\ {\displaystyle \sin \alpha -\sin \beta =2\cos {\alpha +\beta \over 2}\sin {\alpha -\beta \over 2}} \\ {\displaystyle \cos \alpha +\cos \beta =2\cos {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}} \\ {\displaystyle \cos \alpha -\cos \beta =-2\sin {\alpha +\beta \over 2}\sin {\alpha -\beta \over 2}}\)
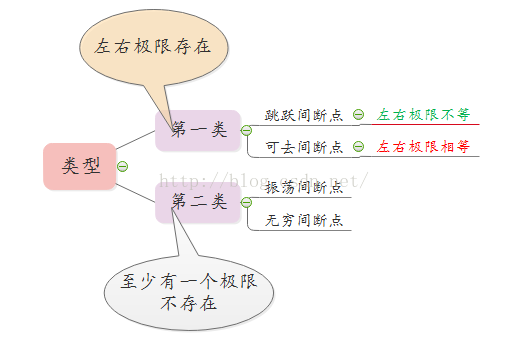
- 在 $x_0$ 无定义;
- $\lim_{x \to x_0}f(x)$ 不存在;
- $\lim_{x \to x_0}f(x) \neq f(x_0)$
1.9 闭区间连续函数的性质 2 28:03
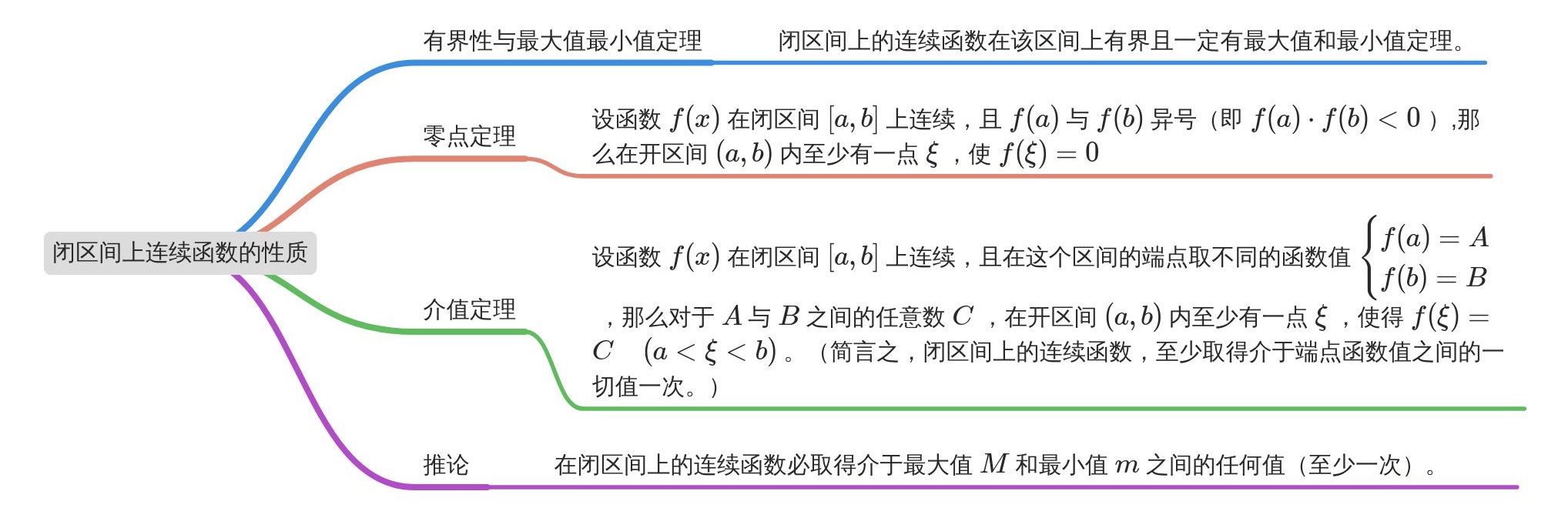
2.1 导数定义 23:28
几种记法:
- \[\left.y^{\prime}\right|_{x={x_0}}\]
- \[f^{\prime}\left(x_{0}\right)\]
- \[\left.\frac{d y}{d x}\right|_{x=x_{0}}\]
- \[\left.\frac{d f(x)}{d x}\right|_{x=x_{0}}\]
2.1 常用求导公式举例 34:17
常见函数的导数
- $f(x)=C$,$C$ 是常数,$f'(x)=0$。
- $f(x)=x^n$,$f'(x)=nx^{n-1}$
- $f(x)=\sin x$,$f'(x)=\cos x$
- $f(x)=\cos x$,$f'(x)=-\sin x$
- $f(x)=a^x$,$f'(x)=a^x\ln a$
- $f(x)=\log_ax$,$f'(x)=\frac{1}{x\ln a}, (a > 0, a \neq 0)$
- $f(x)=\ln x$,$f'(x)=\frac{1}{x}$
- 常数函数的导数处处为零。
- $(x^{\mu})'=\mu x^{\mu-1}$
- $(\sin x)'=\cos x$
- $(\cos x)'=-\sin x$
- $(\tan x)'=\sec^{2}x$
- $(\cot x)'=-\csc^{2}x$
- $(\sec x)'=\tan x\sec x$
- $(\csc x)'=-\cot x\csc x$
- $(a^{x})'=a^{x}\ln a$
- $(e^{x})'=e^{x}$
- $(\log_{a}^{x})'=\frac{1}{x\ln a}$
- $(\ln x)'=\frac{1}{x}$
- $(\arcsin x)'=\frac{1}{\sqrt{1-x^{2}}}$
- $(\arccos x)'=-\frac{1}{\sqrt{1-x^{2}}}$
- $(\arctan x)'=\frac{1}{1+x^{2}}$
- $(arccot x)'=\frac{1}{1+x^{2}}$
- $(arcsecx)'=\frac{1}{x\sqrt{x^{2}-1}}$
- $(arccscx)'=-\frac{1}{x\sqrt{x^{2}-1}}$
2.1 单侧导数 08:32
2.1 导数的几何含义 16:26
导数的几何意义是该函数曲线在这一点上的切线斜率。
- 切线:$y-y_0=f'(x_0)(x-x_0)$
- 法线:$y-y_0=-\frac{1}{f'(x_0)}(x-x_0)$
练习题:导数定义 切线 法线(后期插入)
2.1 可导与连续的关系 09:53
$y=x^{1/3}$ 在 $0$ 点,连续不可导数。
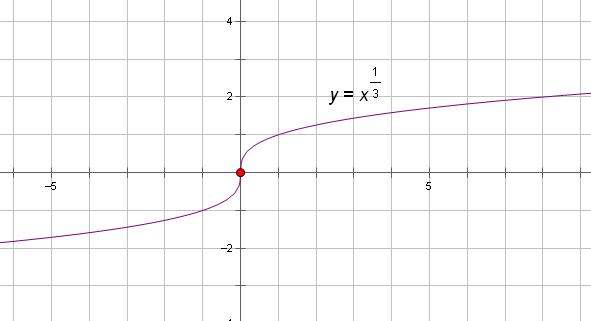
2.2 求导法则(和差积商)28:03
如果函数 $u=u(x)$ 及 $v=v(x)$ 都在点 $x$ 具有导数,那么它们的和、差、积、商(除分母为零的点外)都在点 $x$ 具有导数,且有 \(\begin{cases} [u(x)\pm v(x)]'=u'(x)\pm v'(x) \\ [u(x)v(x)] '=u'(x)v(x)+u(x)v'(x) \\ [\frac{u(x)}{v(x)}]'=\frac{u'(x)v(x)-u(x)v'(x)}{v^2(x)}(v(x)\ne 0) \end{cases}\)
2.2 反函数的求导法则 39:14
反函数的导 $(d\check{a} o)$ 数等于直接函数的导数的倒 $(d \grave{a} o)$ 数。
复合函数求导法则 26:31
链式法则
复合函数求导(补充)03:43
$y=x^x$ 的导数是什么?
\((x^x)'=(e^{x\ln x})'=(1+\ln x)x^x\)
导数公式表 12:24
- $(C)'=0$
- $(x^{\mu})'=\mu x^{\mu-1}$
- $(\sin x)'=\cos x$
- $(\cos x)'=-\sin x$
- $(\tan x)'=\sec^{2}x$
- $(\cot x)'=-\csc^{2}x$
- $(\sec x)'=\tan x\sec x$
- $(\csc x)'=-\cot x\csc x$
- $(a^x)'=a^x\ln a$
- $(e^{x})'=e^{x}$
- $(\log_{a}^{x})'=\frac{1}{x\ln a}$
- $(\ln x)'=\frac{1}{x}$
- $(\arcsin x)'=\frac{1}{\sqrt{1-x^{2}}}$
- $(\arccos x)'=-\frac{1}{\sqrt{1-x^{2}}}$
- $(\arctan x)'=\frac{1}{1+x^{2}}$
-
$(arccot x)'=\frac{1}{1+x^{2}}$
- $(arcsecx)'=\frac{1}{x\sqrt{x^{2}-1}}$
- $(arccscx)'=-\frac{1}{x\sqrt{x^{2}-1}}$
高阶导数 32:17
- $y'$
- $\frac{dy}{dx}$
- $y''$
- $\frac{d}{dx}({\frac{dy}{dx}})$
- $\frac{d(\frac{dy}{dx})}{dx}$
- $\frac{d^2y}{dx^2}$
- $(\frac{dy}{dx})^2$
隐函数求导 28:44
参数方程求导 08:49
练习:高阶导数 参数方程 隐函数求导(后期插入)
微分的定义 23:28
基本微分公式与法则 16:36
$dy=f'(x)dx$
微分的几何意义 12:59
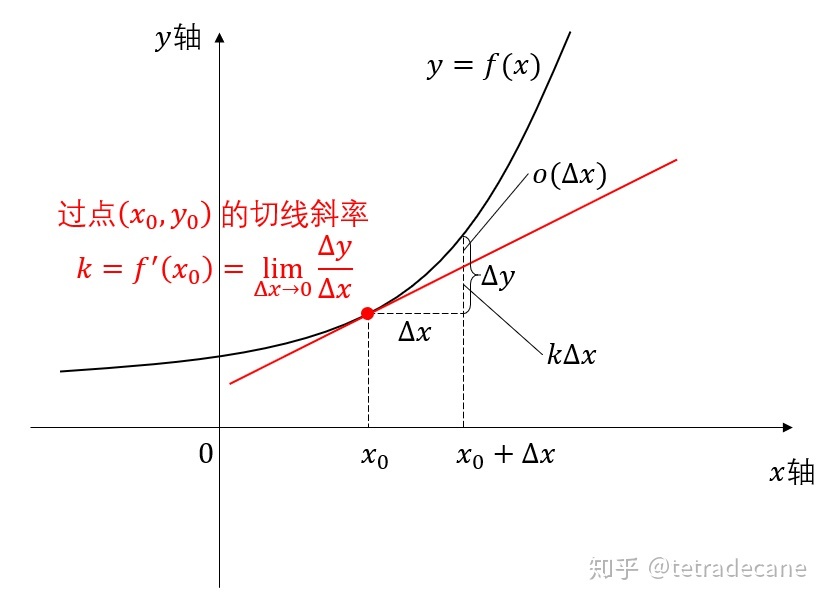
微分在近似计算中的应用 41:26
近似计算公式 $f(x_0+\Delta x)\approx f(x_0)+f'(x_0)\cdot \Delta x$
- $(1+x)^\alpha\approx1+\alpha x$
- $\sin(x)\approx x$ ($x$ 取弧度制)
- $\tan(x)\approx x$
- $e^x\approx x+1$
- $\ln(1+x)\approx x$
微分中值定理 21:31
- 费马引理
- 罗尔中值定理
- 设函数满足以下三个条件:
- $f(x)$ 在闭区间 $[a,b]$ 上连续
- $f(x)$ 在开区间 $(a,b)$ 上可导
- $f(a)=f(b)$
- 则存在 $\xi \in (a,b)$,使得 $f'(\xi)=0$
- 设函数满足以下三个条件:
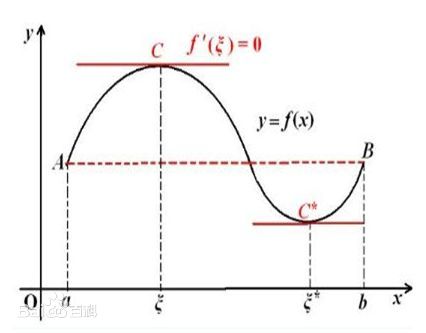
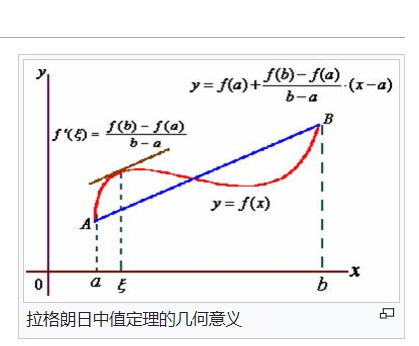
- 拉格朗日中值定理
- 设函数满足以下两个条件:
- $f(x)$ 在闭区间 $[a,b]$ 上连续
- $f(x)$ 在开区间 $(a,b)$ 上可导
- 则存在 $\xi\in (a,b)$,使得 $f'(\xi)=\frac{f(b)-f(a)}{b-a}$
- 设函数满足以下两个条件:
- 柯西中值定理
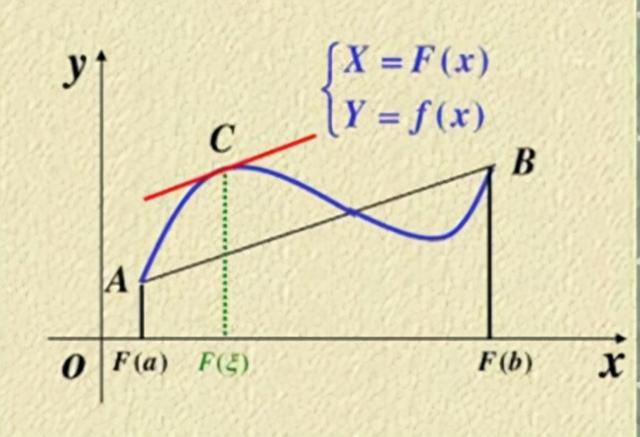
柯西中值定理 14:54
设函数 $f(x),g(x)$ 满足以下条件:
- $f(x),g(x)$ 在闭区间 $[a,b]$ 上连续
- $f(x),g(x)$ 在开区间 $(a,b)$ 上可导
- $\forall x\in(a,b)$ 有:$g'(x)\neq 0$ 则存在 $\xi \in (a,b)$,使等式 \(\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(\xi)}{g'(\xi)}\\\) 成立。
三大微分中值定理的联系与区别:
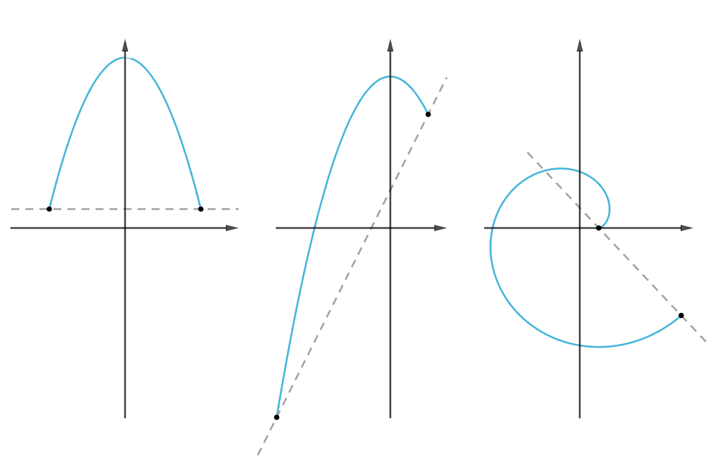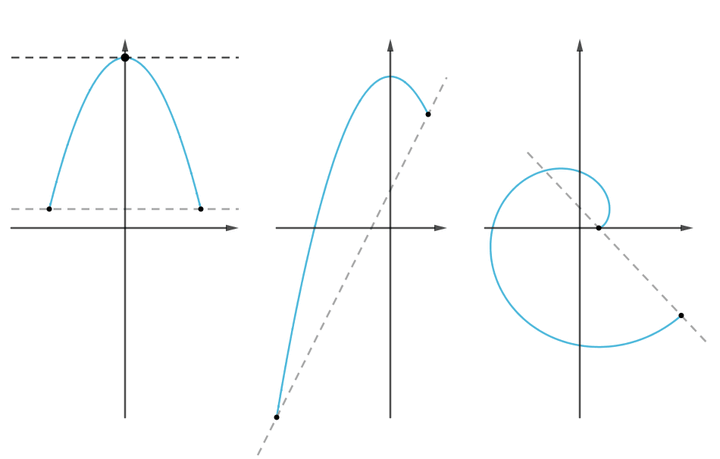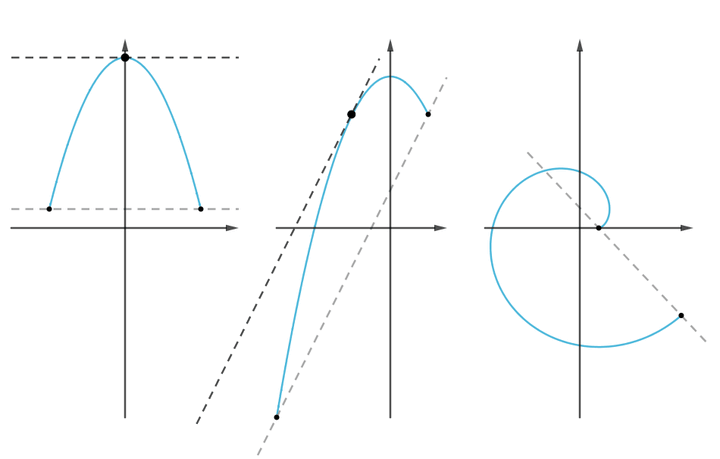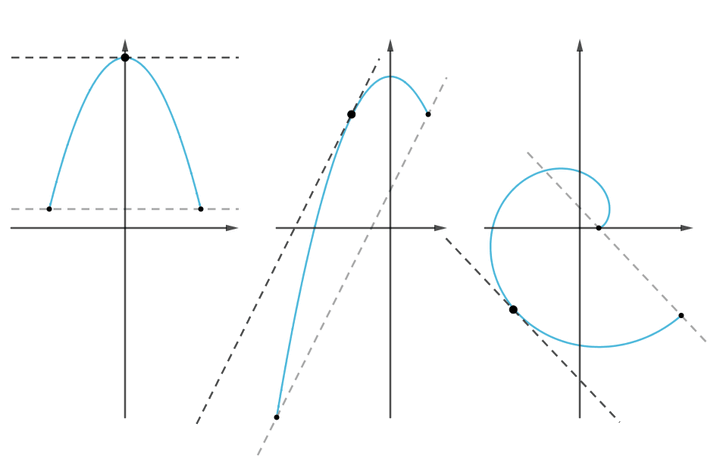
洛必达法则 48:19
洛必达法则的本质是一个定理,它规定,如果一个形如 $\displaystyle \lim_{x \to a}\frac{f(x)}{F(x)}$ 的极限,如果它满足:
- $x$ 趋向于常数 $a$ 时,函数 $f(x)$ 和 $F(x)$ 都趋向于 $0$
- 在点 $a$ 的去心邻域内,$f(x)$ 和 $F(x)$ 的导数都存在,并且 $F'(x) \neq 0$
- $\displaystyle \lim_{x \to 0}\frac{f'(x)}{F'(x)}$ 存在
那么: \(\displaystyle \lim_{x \to a}\frac{f(x)}{F(x)}= \lim_{x \to a}\frac{f'(x)}{F'(x)} \\\)
也就是当变量趋向于一个常数时,如果分子分母函数的导数存在,那么我们可以用导数的极限比值来代替原函数的比值。
求极限之前,先要检查是否满足 $0/0$ 或 $∞/∞$ 型构型,不然滥用洛必达法则会出错。当不存在时(不包括 $∞$ 情形),就无法用洛必达法则,这时称洛必达法则不适用,得从另外途径求极限,例如利用泰勒公式去求解。
$x \rightarrow+\infty$ $\ln x$ < $x^{n}$ < $e^{x}$
泰勒公式 44:29
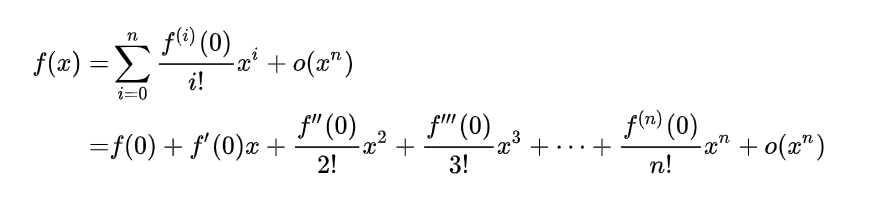
泰勒公式,是一个用函数在某点的信息描述其附近取值的公式。 如果函数满足一定的条件,泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。
泰勒定理(Taylor's Theorem)
皮亚诺(Peano)余项的麦克劳林(Maclaurin)公式 设 $f(x)$ 在 $x=0$ 附近有 $n$ 阶导数,则在 $x=0$ 附近有 $f(x)=\sum_{i=0}^n a_ix^i+o(x^n)$,其中 $a_i=\frac{f^{(i)}(0)}{i!}$, 称 $R_n(x)=o(x^n)$ 为皮亚诺余项。
麦克劳林公式(Maclaurin's series)是泰勒公式的一种特殊形式。 泰勒公式,当 $x_0=0$ 时,就是 麦克劳林公式。
八个常用泰勒公式
- $e^x=1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+o(x^3)$
- $\ln(1+x)=x-\frac{1}{2}x^2+\frac{1}{3}x^3+o(x^3)$
- $\sin x=x-\frac{x^3}{3!}+o(x^3)$
- $\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}+o(x^4)$
- $\arcsin x=x+\frac{x^3}{3!}+o(x^3)$
- $\tan x=x+\frac{x^3}{3}+o(x^3)$
- $\arctan x=x-\frac{x^3}{3}+o(x^3)$
- $(1+x)^m=1+mx+\frac{m(m-1)}{2}x^2+o(x^2)$
函数的单调性 24:33
$y=f(x)$,$[a,b]$ 连续,$(a,b)$ 可导。
- $f'(x)\geq 0$ 等号在有限点,单调增加。
$f'(x)$
- $f'(x)=0$ 驻点 。
- 导数不存在的点。
函数的凹凸性和拐点(后期插入)
极值及其求法 39:28
- 极值,领域内,最小(大),不唯一。
- 最值,整个区域内,最小(大),唯一。
步骤:
- 求 $f'(x)$
- 求驻点和不可导点
- 考查左右导数符号是否变化
函数图形的绘制 1:00:50
求定义域、求间断点、求渐近线、求导计算单调性、求二阶导研究凹凸性……
函数曲线的上升或下降反映了函数的单调性,而曲线在上升或下降过程中,还存在一个弯曲方向的问题,如图:
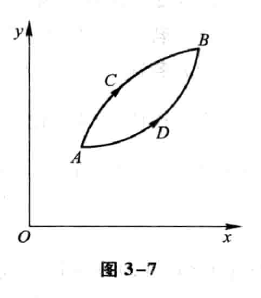
曲率 29:54
曲线的曲率(curvature)就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。 曲率越大,表示曲线的弯曲程度越大。曲率的倒数就是曲率半径。
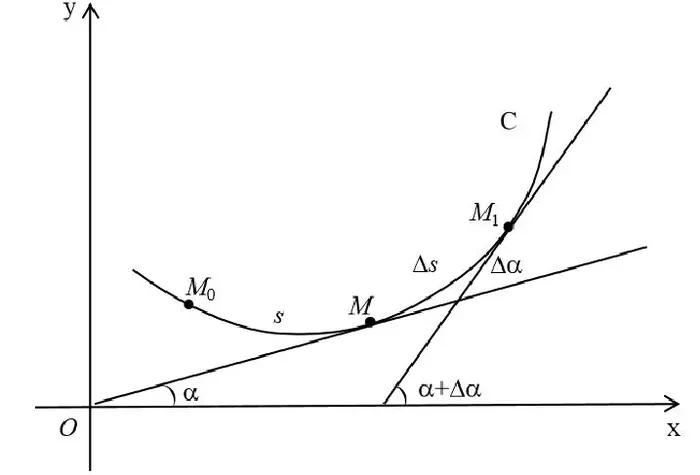
已知函数 $f(x)$ 在 $x_0$ 点有二阶导数 $f''(x_0)$,且 $f''(x_0)\ne 0$,则此点有密切圆,其半径为: \(r=\frac{\left(1+\left(f'(x_0)\right)^2\right)^\frac{3}{2}}{\left|f''(x_0)\right|}\\\) 此时,曲线的 曲率 也就是密切圆的曲率,为: \(K=\frac{1}{r}=\frac{\left|f''(x_0)\right|}{\left(1+\left(f'(x_0)\right)^2\right)^\frac{3}{2}}\\\) 所以密切圆也称为曲线的 曲率圆,半径 $r$ 称为 曲率半径。
不定积分的定义 29:44
连续的函数一定有原函数。
积分表 14:41
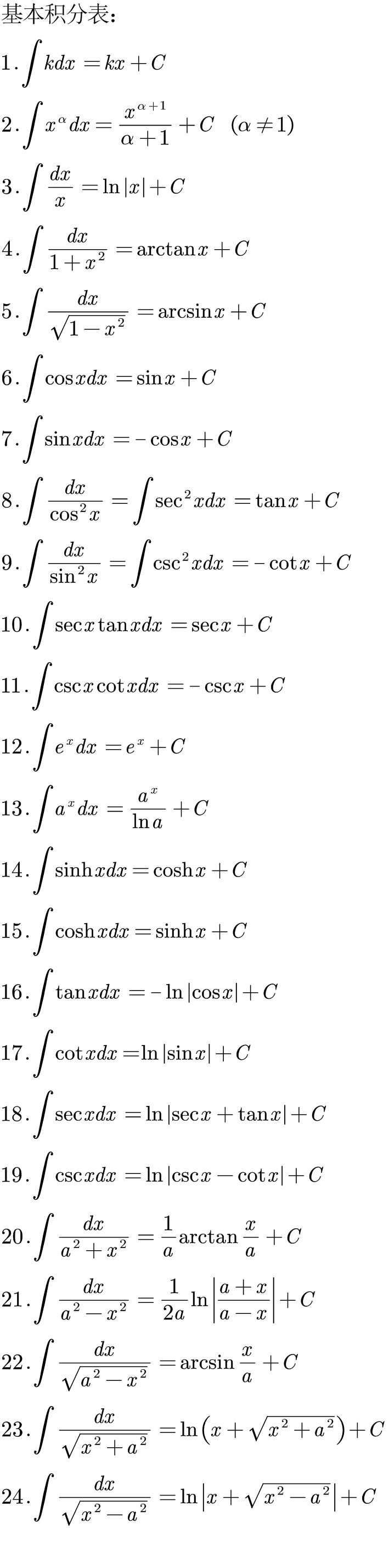

抖肩舞 02:27
不定积分的性质 34:23
完成。
$(1/1)^2+(1/2)^2+(1/3)^2+……=(π^2)/6$,为什么结果与 $π$ 有关?
第一类换元积分法 1:02:03
凑。
- $d$ 的里面可以任意加减常数。
第二类换元积分法 53:16
第一、二类积分法分别从积分变量和被积函数的角度,对积分式进行变形,从而做到了简化积分计算的目的。 为方便理解,我喜欢把两类换元法叫凑微分和拆微分。
- 第一类换元积分为凑微分。拆被积函数给后面凑一个好用的 $dx$。
- 第二类为拆微分。被积函数中的 $x$ 通通换元为 $Ψ(u)$,后面的 $dx$ 拆为 $ ψ′(u)du$。
e 和 π 之间竟有一种意想不到的联系
涉及到空间的必有 $π$(包括但不限于曲线、并列、共同存在等) 涉及到时间的必有 $e$(包括但不限于变化、递进、稠密连续等) 另外,涉及到信息的必有有理数。
baidu 圆周率派表达的其实就是时空性质,派本身表平滑时空,大于派是扩散也就是凸面时空,也就是大尺度上的星云星系相互加速远离现象,而小于派则相反,表现为引力时空,所有非平滑时空都会趋向于平滑继而向相反的方向发展,此既宇宙生生不息的根本,而理想的平滑时空本身是不存的,就象直线亦不存在一样,同理,所有正统的欧氏几何空间也是不存在的,它们只是一种抽象的用来探索真正存在的时空的工具,作为参照物而存在。
分部积分法 55:33
令 $u$ 与 $v$ 是两个以 $x$ 为自变量的可微函数,那么 \((uv)'=u'v+uv'\) \(uv=\int (uv)' dx=\int u'vdx+\int uv'dx\)
优先级:
- $e^x$
- $\sin x$ $\cos x$
- $x^n$
有理函数积分 40:39
形如 $\int \frac{P_{n}(x)}{Q_{m}(x)} \mathrm{d} x(n<m)$ 的积分称为有理函数的积分,其中 $P_{n}(x)$,$Q_{m}(x)$ 分别是 $x$ 的 $n$ 次多项式和 $m$ 次多项式。方法 先将 $Q_{m}(x)$ 因式分解,再把 $\frac{P_{n}(x)}{Q_{m}(x)}$ 拆成若干干最简有理分式之和。
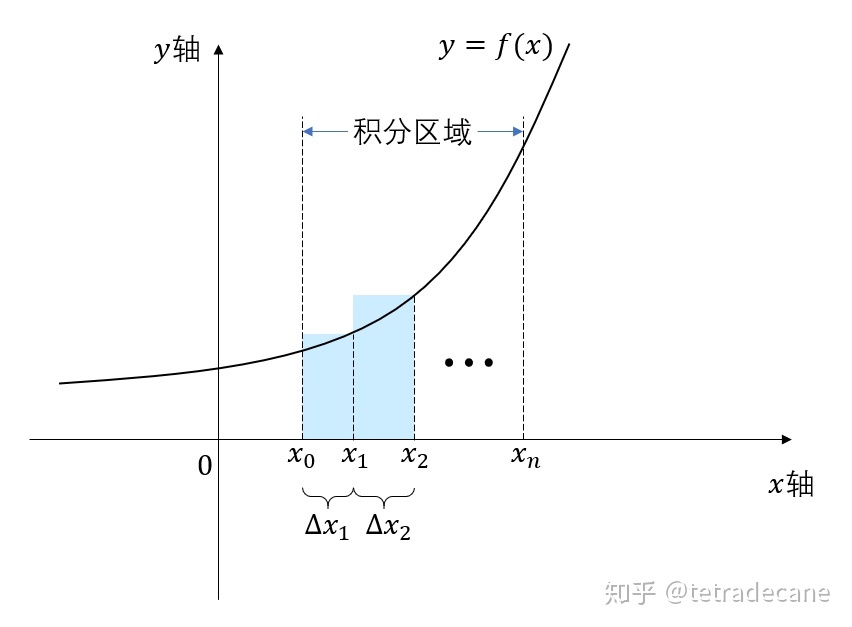
【五-1】定积分的概念 46:38
【五-2】定积分的性质 32:15
完成。
【五-3】微积分基本公式 52:15
令 $u=\varphi(x)$,那 $\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}=\frac{d}{du}\int_{0}^{u}f(t)dt\cdot u'=f(u)u'=f(\varphi(x))\varphi'(x)$
\[\Phi(x)=\int_{a}^{x} f(t) d t\] \[\Phi^{\prime}(x)=\frac{d}{d x} \int_{a}^{x} f(t) d t=f(x)\]牛顿莱布尼茨定积分公式
\({\color{red }{\boxed {\int_{a}^{b}f(x){\rm d}x =F(b)-F(a)} }}\)
连续函数 $f(x)$
在推导中学习 —— 牛顿-莱布尼茨公式
【五-4】定积分的换元法 1:34:25
\[\int_{a}^{b} f(x) d x=\int_{\alpha}^{\beta} f[\varphi(t)] \varphi^{\prime}(t) d t\]- 引入换元函数
- 上下限也跟着变
解答:
令 $x=a\sin t$,$dx=a\cos t d t$,$x=0$ 时,$t=0$ 时,$x=a$,$t=\frac{\pi}{2}$。
则 \(\int_{0}^{a} \sqrt{a^{2}-x^{2}} d x= \int_{0}^{\pi/2} \sqrt{a^2-a^2\sin^2 t} a \cos t dt= \frac{\pi}{4} a^2\)
三角恒等式
- $sin^2x+cos^2=1$
- $1+tan^2x=secx$
- $1+cot^2x=cscx$
三角函数辅助角公式 asinx+bcosx=√(a²+b²)[asinx/√(a²+b²)+bcosx/√(a²+b²)] asinx+bcosx=√(a+b)sin[x+arctan(b/a)](a>0)。
【五-5】定积分的分部积分法 18:36
\[\int_{a}^{b} u dv = \left. uv \right|_{a}^{b} - \int_{a}^{b} v du\]【五-6】无穷限的反常积分 26:08
from
\(\begin{align*} \int_0^{+\infty}\frac{x}{e^x+1}{\rm d}x &=\int_0^{+\infty}x\sum_{n=1}^{\infty}(-1)^{n+1}e^{-nx}{\rm d}x\\ &=\sum_{n=1}^{\infty}(-1)^{n+1}\int_0^{+\infty}xe^{-nx}{\rm d}x\\ &=\sum_{n=1}^{\infty}\frac{(-1)^{n}}{n}\int_0^{+\infty}x{\rm d}e^{-nx}\\ &=\sum_{n=1}^{\infty}\frac{(-1)^n}{n}\left(xe^{-nx}\bigg|_0^{+\infty}-\int_0^{+\infty}e^{-nx}{\rm d}x\right)\\ &=\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}\\ &=\frac{\pi^2}{12}. \end{align*}\\\)
【五-7】无界函数的反常积分 27:29
反常积分:注意瑕点。
瑕积分的欺骗性,一定要关注 瑕点。
【五-8】伽马函数 07:01

伽马函数满足以下递推关系: \(\Gamma(z+1)=z\Gamma(z)\)
当 $z$ 为整数时,有 \(\color{red}{\Gamma(z+1)=z(z-1)\cdots 2\cdot1=z!}\)
【六-1】定积分的应用-元素法 16:11
不规则 求 面积 & 体积。
【六-2】定积分应用–求面积 37:45
【六-3】定积分应用–求面积(二)10:22
【六-4】定积分应用–求面积极坐标情形 05:43
极坐标下的面积。
找交点,确定角度,计算面积 若 $0<\rho<\rho(\theta)$,$\alpha<\theta<\beta$: 则此曲线所围绕面积为
\[S=\frac{1}{2}\int_{\alpha}^{\beta}\rho^{2}(\theta)d\theta\]【六-5】定积分应用–旋转体体积 1:16:42
为什么用定积分求椭圆绕 x 轴旋转的体积和绕 y 轴旋转的体积不一样?
找一个狭长的椭圆,按短轴转可以转出一个大圆盘,按长轴转只是一个细棒。 不需要微积分,拉伸变换拉一拉就出来了。
- 长轴半长 $a$ 短轴半长 $b$
- 圆盘体积 \(4\pi/3*a^3*(b/a)~a^2*b\)
- 细棒体积 \(4\pi/3*b^3*(a/b)~a*b^2\)
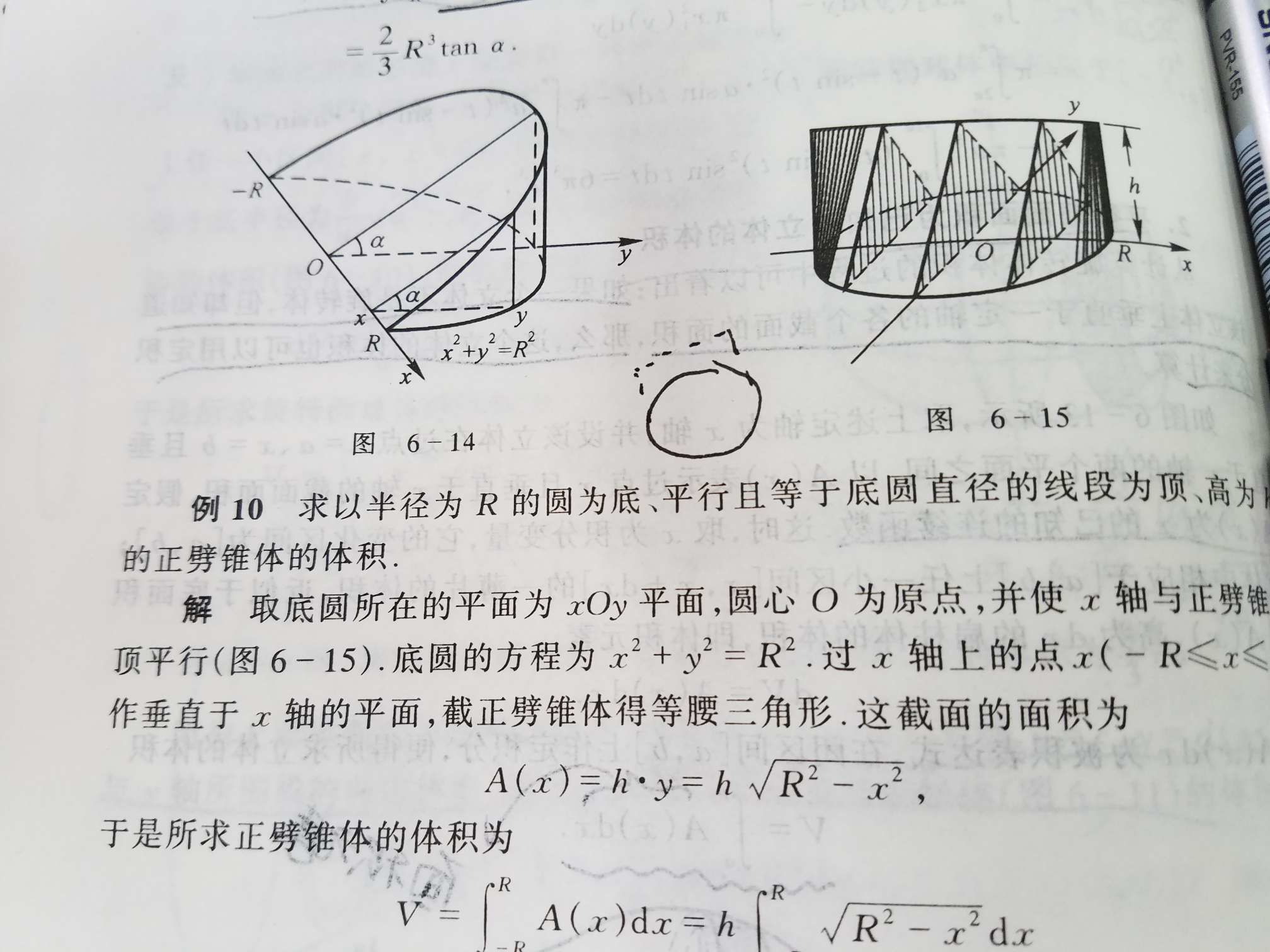
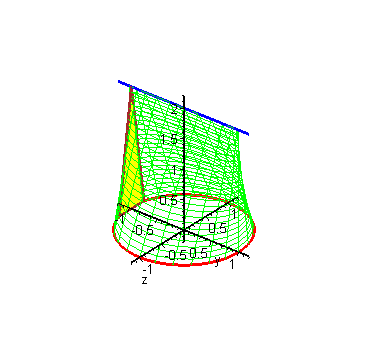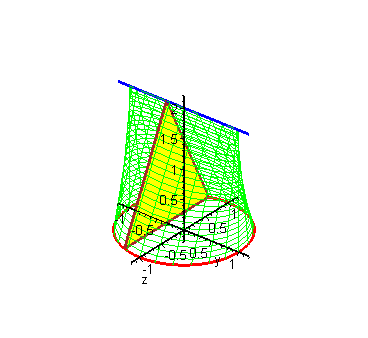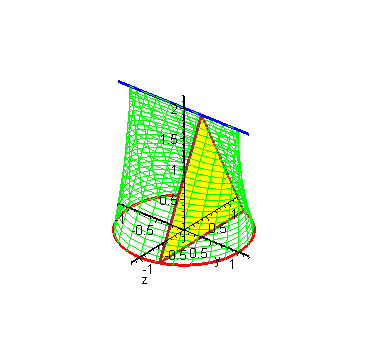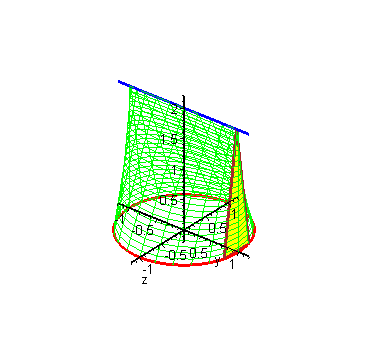
正劈锥体
【六-6】定积分应用–平面曲线的弧长 41:05
完成。
【新】定积分应用–物理学 34:13
完成。
【七-1】微分方程的基本概念 08:50
完成。
【七-2】可分离变量的微分方程 12:28
完成。
【七-3】齐次方程 31:20
$ y/x$ 整体出现。
- $u=y/x$
- $y=xu$
- $dy/dx=u+x(du/dx)$
可转化为齐次的方程 :
\(\frac{dy}{dx}=\frac{a_{1}x+b_{1}y+c_{1}}{a_{2}x+b_{2}y+c_{2}}\tag1\)
将微分方程转换为齐次方程,再将齐次方程转换为可分离变量方程,进而求解微分方程。
【七-4】一阶线性微分方程 28:23
\[\frac{dy}{dx}+p(x)y=Q(x)\]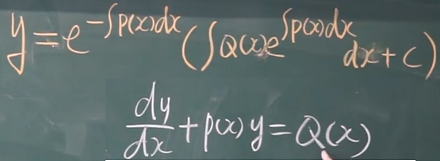
伯努利 方程 \(\frac{\mathrm dy}{\mathrm dx}+P(x)y=Q(x)y^n(n\not=0,1).\)
【七-5】可降阶的高阶微分方程 17:23
\[y^{(n)}=f(x)\]$\frac{d p}{d y} \cdot \frac{d y}{d x}$ 理解为求导,不可以消掉,但是你理解为微分,就可以消掉了。
【七-6】常系数线性齐次微分方程 24:17
$y^{\prime \prime}+p y^{\prime}+q y=0$
特征方程:$r^2+pr+q=0$
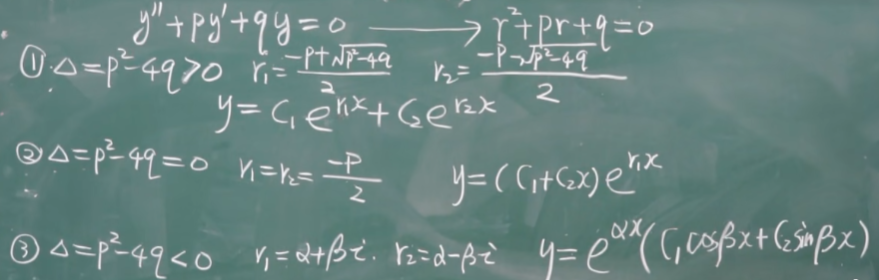
解特征方程实际上是在寻找线性变换的“轴”。
note
【七-7】补充证明过程(可略)22:05
【八-1】向量及线性运算 40:23
【八-2】空间直角坐标系 23:16
【八-3】向量模 两点距离 05:59
【八-4】方向角方向余弦 45:59
方向角和方向余弦公式是 $a°=(cosα)i+(cosβ)j+(cosγ)k$,方向余弦是指在解析几何里,一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。

【八-5】数量积 30:05
- 点乘,也叫数量积。结果是一个向量在另一个向量方向上投影的长度,是一个标量。
- 叉乘,也叫向量积。结果是一个和已有两个向量都垂直的向量。模等于由向量 $a$ 和向量 $b$ 构成的平行四边形的面积。
以我比较熟悉的图形学而言,一般点乘用来判断两个向量是否垂直,因为比较好算。也可以用来计算一个向量在某个方向上的投影长度,就像定义一样。
叉乘更多的是判断某个平面的方向。从这个平面上选两个不共线的向量,叉乘的结果就是这个平面的法向量。 在二维空间中,叉乘还有另外一个几何意义就是:$|a \times b|$ 的模等于由向量 $a$ 和向量 $b$ 构成的平行四边形的面积。
人类对于高维世界是缺乏想象的,唯一个工具就是数学。 线性代数和向量空间理论可以帮助我们理解二维和多维空间中的向量运算和线性变换。 微积分和拓扑学可以用于研究高维空间中的函数、曲线和曲面的性质。 在物理学和量子力学中,高维度空间的数学模型被用来描述粒子和场的行为。
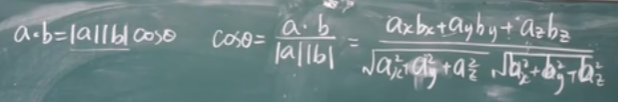
未来几年,将是改革开放以来就业形势最严峻的时刻。 如果不能妥善解决这个问题,未来 5 年每年继续积累 500 万青年失业人员的话,意味着到 2028 年社会可能积压 5000 万左右的青年失业人员。 那么失业将会成为一个普遍性的社会问题,每四五个家庭就有一个失业人员,进而引发一系列深层危机。
【八-6】向量积 33:05
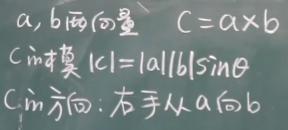
【八-7】平面及其方程 43:59
克莱姆法则:如果一个方程组符合以下两个条件:
- n 个方程,n 个未知量;
- 系数行列式 D 不等于 0。那么其中一个未知量 m 的值为 $\frac{D_m}{D}$。
齐次方程组: 定理 1:如果一个方程组是齐次方程组,方程个数与未知量个数相等,并且系数行列式不等于 0,那么这个方程组只有零解。 定理 2:方程个数与未知量个数相同的齐次方程组有非零解,是,该方程组的系数行列式等于 0,的充分必要条件。
【八-8】平面的一般方程 17:15
截距式方程。
【八-9】两平面的夹角 19:50
【八-10】空间直线及其方程 15:02
【八-11】两直线的夹角 & 直线与平面的夹角 12:12
完成。
杂例 50:49
平面束。
曲面及其方程 14:03
旋转曲面 29:59
柱面 07:28
二次曲面 32:13
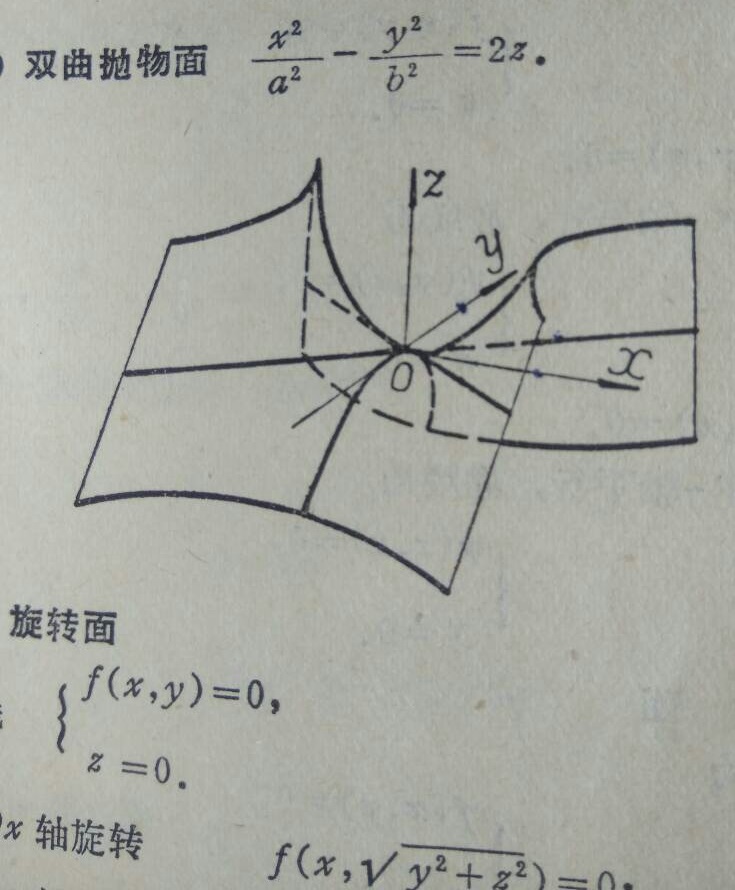
马鞍面就是双曲抛物面
空间曲线及其方程 26:23
【九-1】多元函数的基本概念–平面点集 23:34
【九-2】n 维空间 09:59
【九-3】多元函数的极限 34:39
【九-4】偏导数 43:41
【九-6】全微分 46:01
偏导数存在是可微的必要不充分条件。
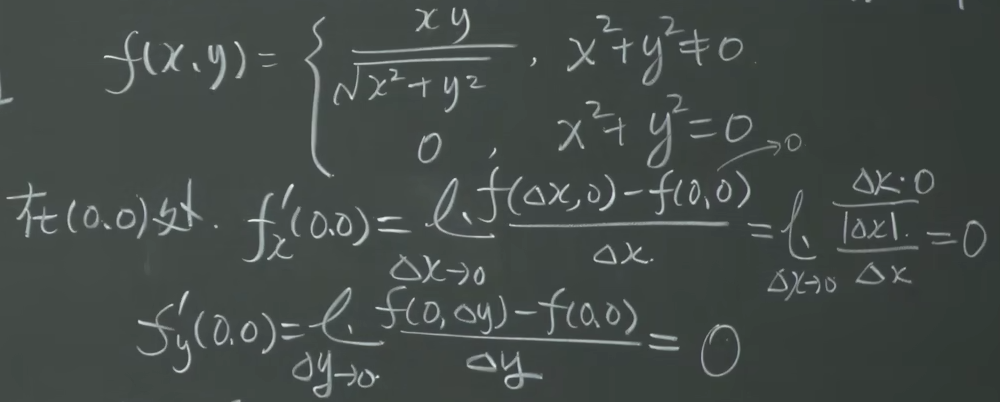
近似计算:
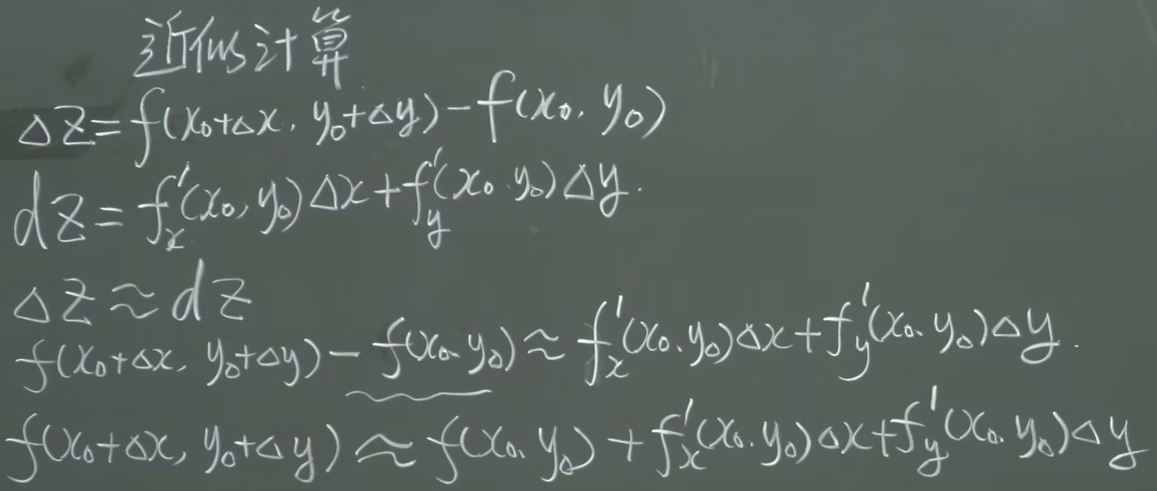
【九-7】多元复合函数求导(理论讲解)30:32
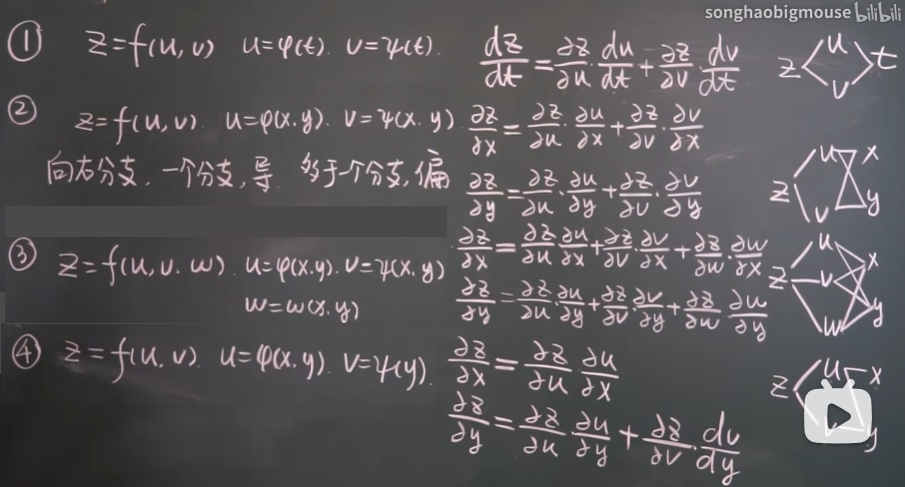
【九-8】多元复合函数求导(例子讲解)11:59
【九-9】隐函数求导(一个方程)28:31
【九-10】隐函数求导(方程组)37:27
【9-10】隐函数求导(方程组)例 3 符号更正 00:21
【九-11】一元向量值函数及其导数 46:56
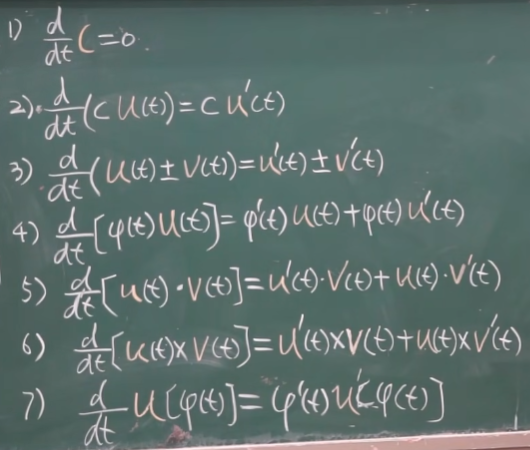
【九-12】空间曲线的切线与法平面 26:32
克莱姆法则,又译克拉默法则(Cramer's Rule)是线性代数中一个关于求解线性方程组的定理。
已知 \(\begin{matrix} ax+by=e \\ cx+dy=f \\ \end{matrix}\),矩阵表示为 \(\left [\begin {matrix} a&b\\ c&d \end{matrix} \right ] \left [\begin {matrix} x\\ y \end{matrix} \right ]= \left [\begin {matrix} e\\ f \end{matrix} \right ]\), 当 \(\left |\begin {matrix} a&b\\ c&d \end{matrix} \right |\ne 0\) ,x 和 y 可以根据克莱姆法则求出:
\[x={\frac{\left |\begin {matrix} e&b\\ f&d \end{matrix} \right |} {\left |\begin {matrix} a&b\\ c&d \end{matrix} \right |}} ={\frac{ed-bf}{ad-bc}}\] \[y={\frac{\left |\begin {matrix} a&e\\ c&f \end{matrix} \right |} {\left |\begin {matrix} a&b\\ c&d \end{matrix} \right |}} ={\frac{af-ec}{ad-bc}}\]【九-13】空间曲面的切平面与法线 13:55
【九-14】方向导数 53:04
-
方向导数存在,偏导不一定存在,一个直线,一个射线。
- 多元函数,偏导存在,并不一定连续。
- 可微,则 偏导一定存在。
- 偏导存在且连续,则 可微。
- 可微,则 连续,方向导数必存在。
【九-15】梯度 30:42
【九-16】方向导数和梯度的解释 11:24
【九-17】梯度(例题 #1)14:22
【九-18】梯度(例题 #2)06:36
【九-19】多元函数的极值 20:50

【九-20】数量场向量场 36:46
【九-21】多元函数的最值 09:10
【九-22】条件极值 拉格朗日乘数法(理论讲解)19:29

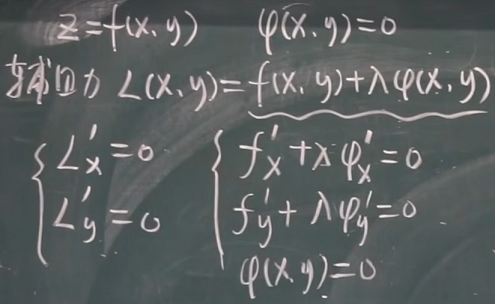
https://www.zhihu.com/zvideo/1385266955763380224
【九-23】极值例题 15:14
【十-1】二重积分的定义 24:21
【十-2】二重积分的性质 14:43
【十-3】二重积分的计算(直角坐标系)1:20:22
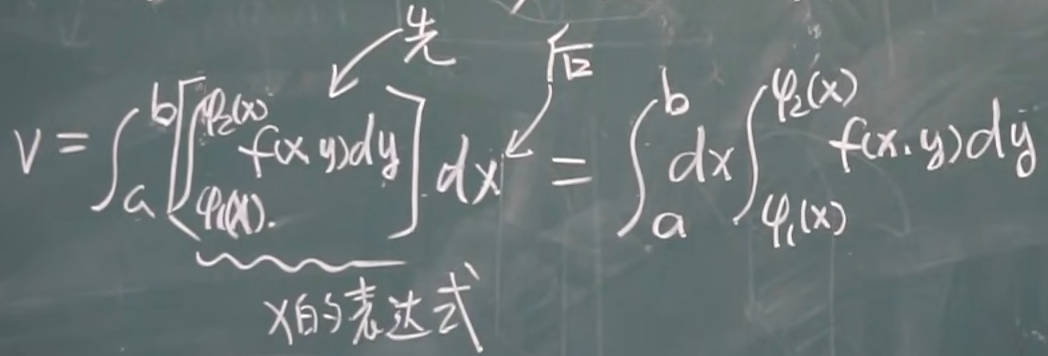
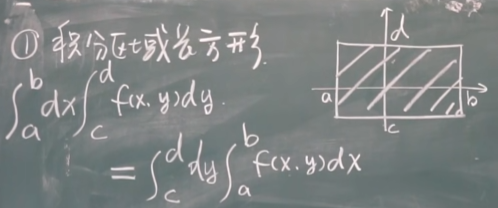
【十-4】极坐标介绍 1 35:25
【十-5】极坐标介绍 2 21:32
【十-6】二重积分(极坐标)58:30
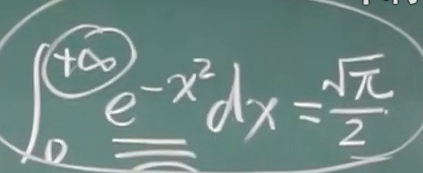
而先生每每讲到精妙之处,学生皆不禁有所共鸣,掌声不绝于耳,报以妙哉之言语。
什么时候用极坐标:
- 积分区域是圆、圆环或者扇形。
- 被积表达式是 $f(x^2+y^2)$、$f(x/y)$、$f(y/x)$。
【十-7】极坐标例题 07:13
【十-8】二重积分的换元法 1:00:05

这个例题经典,雅可比行列式就是两个空间变换的拉伸比。
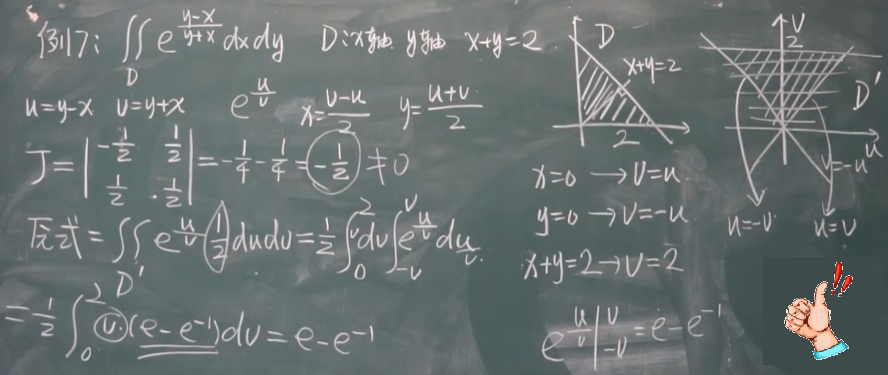
什么时候用?
- 被积函数不好积分;
- 积分区域不好表示。
【十-9】三重积分的定义 14:23
一维是长度,二维是面积,三维是体积,四维是啥?
\[\int_a^b f(x) d x\] \[\iint_D f(x, y) d \sigma\] \[\iiint_{\Omega} f(x, y, z) d v\]【十-10】密度均匀 && 不均匀的理解 14:05
【十-11】三重积分的计算(直角坐标系)35:55
【十-12】例 2 11:12
【十-13】柱面坐标 30:40
【十-14】三重积分球面坐标(插入了新例题 )28:34
\[d v=d x d y d z=r^2 \sin \varphi d r d \varphi d \theta\]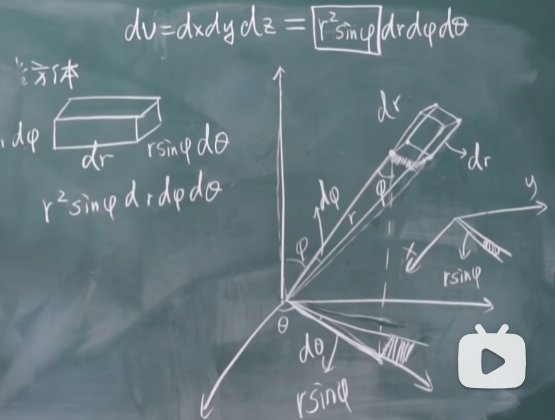
【十-15】三重积分的应用(求曲面的面积)新增加了证明 19:58
【十-16】重积分应用(求质心)16:03
【十-17】重积分应用(求转动惯量)04:34
【十-18】重积分应用(求引力)16:05
【十一(1)】对弧长的曲线积分(概念与性质)14:17
【十一(2)】曲线积分的计算 26:32
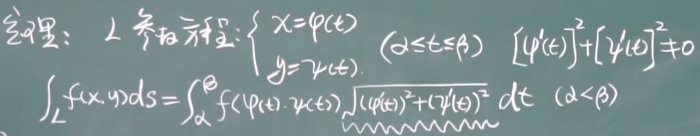
【十一(3)】对坐标的曲线积分(概念和性质)26:08
【十一(4)】对坐标的曲线积分(计算)20:44
【十一(5)】例题 30:08
【十一(6)】两类曲线积分的联系 18:01

【十一(7)】格林公式的定义和证明 1:02:08
\[\oint_{L^+}Pdx+Qdy=\iint\limits_{D}(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy.\] \[\oint_{C}Pdx+Qdy=\iint_D\left( \frac{\partial Q}{\partial x} -\frac{\partial P}{\partial y}\right)dxdy\]
【十一(8)】格林公式的计算 44:53
格林公式的计算。老师说:你吃了一个胡萝卜,然后又吃了一只鸡蛋,第二天出来的东西,大概能知道什么东西。但是反过来就非常困难,并不能推断出你昨天吃了啥。

【十一(9)】对面积的曲面积分 1:08:13
| 积分学 | 定积分 | 二重积分 | 三重积分 | 曲线积分 | 曲面积分 |
| 积分域 | 区间 | 平面域 | 空间域 | 曲线弧 | 曲面域 |
- 曲线积分
- 对弧长的曲线积分(一型)
- 对坐标的曲线积分(二型)
- 曲面积分
- 对面积的曲面积分(一型)
- 对坐标的曲面积分(二型)
【十一(10)】第二类曲面积分的计算及两类曲面积分的关系 1:33:29
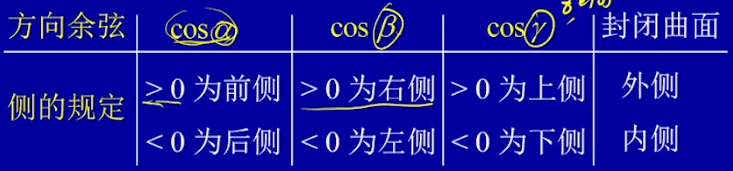
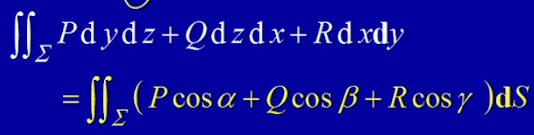
【十一(11)】高斯公式 散度 通量 52:28
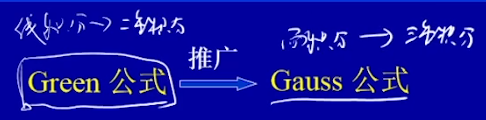
高斯公式(Gauss formula)
- 定积分的概念从计算“曲边梯形的面积”等问题引入
- 二重积分从计算“曲顶柱体体积”引入
- 三重积分则是从求“三维空间中的有界物体的质量”引入的
- 第一类曲线积分从求“物质曲线的质量”中引入
- 第二类曲线积分从计算“力场做功问题”引入
- 第一类曲面积分从求“物质曲面质量问题”引入
- 第二类曲面积分则是从“讨论流量问题”引入
旋度 Curl 散度 Divergence 通量。


【十二(1)】常数项级数的概念和性质 1:10:05
【十二(2)】正项级数(一)47:17
等比 调和 P
【十二(3)】正项级数(二)1:08:51
【十二(4)】交错级数 25:32
【十二(5)】任意项级数 28:17
【十二(6)】幂级数(1)42:17
【十二(7)】幂级数(2)51:50
【十二(8)】幂级数的运算 15:56

性质 3 收敛半径相同。
这里突然和积分联系起来了。
【十二(9)】例题 2 10:03
【十二(10)】函数展成幂级数(1)20:57
【十二(11)】函数展成幂级数(2)29:27

【十二(12)】例题讲解 31:10
离心何以赠,自有玉壶冰。
2023.08.22 毕业于 哔哩哔哩大学。
参考资料快照
- https://www.bilibili.com/video/BV1Eb411u7Fw
- https://www.cnblogs.com/linxd/p/4955530.html
- https://www.a.tools/Tool.php?Id=469
- https://spaces.ac.cn/latex.html/comment-page-1
- https://zuotu.91maths.com/
- https://copyfuture.com/blogs-details/20211118231641378g
- https://blog.csdn.net/weixin_43310853/article/details/104566595
- https://blog.csdn.net/xuchaoxin1375/article/details/125392308
- https://wuli.wiki/changed/limff.html
- https://zhuanlan.zhihu.com/p/259893215
- https://zhuanlan.zhihu.com/p/355228120
- https://zhuanlan.zhihu.com/p/265518833
- https://zhuanlan.zhihu.com/p/89843248
- https://www.zhihu.com/question/265518395/answer/1441563740
- https://zhuanlan.zhihu.com/p/201720785
- https://www.zhihu.com/question/405112095/answer/1320312884
- https://zhuanlan.zhihu.com/p/47436090
- https://www.zhihu.com/question/22102732/answer/2493308582
- https://www.zhihu.com/question/530158369/answer/2461156590
- https://baijiahao.baidu.com/s?id=1736847468931154687
- https://zhuanlan.zhihu.com/p/142909054
- https://www.zhihu.com/question/538493369/answer/2542853013
- https://zhuanlan.zhihu.com/p/466806302
- https://www.bilibili.com/video/BV1KMRJYrEBG
- https://www.oscaner.com/skill/others/mathjax-symbol.html
- https://www.zhihu.com/zvideo/1385266955763380224
- https://www.zhihu.com/question/22674439/answer/185939984
- 机器学习笔记 -- 机器学习资源(进行中) | 26 Jul 2025
- MATHEMATICS -- 生成模型数学 —— 概率论基础 | 27 Sep 2024
- MATHEMATICS --《线性代数》奇异值分解(SVD) | 04 Apr 2024
- MATHEMATICS --《概率论与数理统计》宋浩老师(已完成) | 22 Mar 2024
- MATHEMATICS -- 难懂的数学(已完成) | 10 Sep 2022
- MATHEMATICS --《线性代数》宋浩老师(已完成) | 23 Aug 2022
- MATHEMATICS --《高等数学》同济版 宋浩老师(已完成) | 13 Aug 2022
- 机器学习笔记 -- 线性代数 & 微积分 & 概率论与统计学(唐宇迪) | 01 Sep 2020
- 机器学习笔记 -- 环境搭建 & 数学基础 | 29 Aug 2020
 .
.