MATHEMATICS -- 生成模型数学 —— 概率论基础
了解香农熵,交叉熵和 KL 散度 https://www.bilibili.com/video/BV1JY411q72n/
因为有真实分布,所以用交叉熵。如果没有真实分布,请用 KL 散度。
信息熵就是某个随机事件的信息的期望值,同时也是最优编码的期望长度。 通过计算,可以知道,Huffman 编码就是最优的前缀编码。
信息熵
描述信息源各可能事件发生的不确定性。
\[H(X)=-\sum_{i=1}^n P\left(x_i\right) \log _2 P\left(x_i\right)\]信息量是对某个已经发生的事件而计算的,当我们设定的是某一个随机变量,其包含所有事件发生的可能,那么信息熵的定义就是,这些事件,在概率发生的情况下,带来的平均信息量。
\[H(X)=-\sum_{i=1}^n P\left(x_i\right) \log _2 P\left(x_i\right)=-\mathbb{E}\left[\log _2 P(X)\right]\]KL 散度(相对熵)
一种用于衡量两个概率分布之间的差异的指标。
\[K L(q \| p)=\sum q(x) \log \frac{q(x)}{p(x)}=\int q(x) \log \frac{q(x)}{p(x)} d x\]其表示的是概率分布 $q$ 跟概率分布 $p$ 的相似性。
我们把 KL 散度的公式转化一下,
\[\begin{aligned} K L(q \| p) & =\sum q(x) \log \frac{q(x)}{p(x)} \\ & =\sum q(x)[\log q(x)-\log p(x)] \end{aligned}\]我们可以发现这个公式跟信息熵的公式相当之像, 如果从信息熵的角度去看的话($\log$ 底数取 $2$),其就可以表达成两个概率分布的信息熵的差值。
性质:非负性,$K L(q || p) \geq 0$。等于 $0$ 时表示两个概率分布相等。
性质:非对称性,$K L(q || p) \neq K L(p || q)$。
Cross-Entropy(交叉熵)和 KL-Divergence(相对熵,Kullback-Leibler 散度)
Cross-Entropy(交叉熵)和 KL-Divergence(相对熵,Kullback-Leibler 散度) 在信息论和机器学习中都用于衡量概率分布之间的差异,但它们有本质区别:
- 定义不同 :
- 交叉熵(Cross-Entropy, CE) :衡量两个概率分布之间的不匹配程度,定义为: \(H(P, Q) = -\sum P(x) \log Q(x)\) 其中 $ P(x) $ 是真实分布(ground truth),$ Q(x) $ 是预测分布。
- KL 散度(KL-Divergence, KLD) :衡量一个分布与另一个分布之间的信息损失,定义为: \(D_{KL}(P || Q) = \sum P(x) \log \frac{P(x)}{Q(x)}\) 它表示用 $ Q(x) $ 近似 $ P(x) $ 时,额外消耗的信息量。
- 关系 :
- KL 散度可以表示为交叉熵和熵(Entropy)的差: \(D_{KL}(P || Q) = H(P, Q) - H(P)\) 其中,$ H(P) = -\sum P(x) \log P(x) $ 是熵,表示分布 $ P $ 自身的不确定性。
- KL 散度与交叉熵紧密相关 ,它表示交叉熵与真实分布熵的偏差。
- 最小化交叉熵等价于最小化 KL 散度 (在 $ H(P) $ 固定的情况下)。
- 应用 :
- 交叉熵 常用于分类任务中的损失函数,如神经网络中的 softmax+cross entropy。
- KL 散度 常用于概率分布逼近,例如变分自编码器(VAE)和强化学习中的策略优化。
简而言之,交叉熵直接作为损失,而 KL 散度衡量两个分布的相似程度,优化时 KL 散度通常间接影响交叉熵。 因为有真实分布,所以用交叉熵。如果没有真实分布,请用 KL 散度。
变分自动编码器和变分贝叶斯方法
用一族相对比较简单并且可以参数化的概率分布去近似它,这个近似的过程就叫做变分。 使用近似的概率分布去尝试完成被给定观测变量的情况下对隐变量概率分布的估计的过程就叫变分推理。
Kullback-Leibler(KL) 散度介绍
https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained
在最一般的意义上,神经网络是函数近似器。这意味着你可以使用神经网络来学习各种复杂的功能。使神经网络学习的关键是使用目标函数,该函数可以告知网络运行状况。你可以通过最小化目标函数的损失来训练神经网络。
我们可以使用 KL 散度来最小化近似分布时的信息损失量。将 KL 散度与神经网络相结合,可以让我们学习非常复杂的数据近似分布。一种常见的解决方法称为“变分自编码器”,它学习了近似数据集中信息的最佳方法。
更一般的是变分贝叶斯方法领域。 蒙特卡洛模拟可以有效解决一系列概率问题。尽管蒙特卡洛模拟可以帮助解决贝叶斯推理所需的许多难解积分,但即使这些方法在计算上也非常昂贵。包括变分自动编码器在内的变分贝叶斯方法使用 KL 散度来生成最佳近似分布,从而可以对非常困难的积分进行更有效的推断。
交叉熵 (cross entropy) ,KL 散度的值,到底有什么含义?
https://mp.weixin.qq.com/s/T6FONoAFY2cMQGfbCHpFOQ 信息熵就是某个随机事件的信息的期望值,同时也是最优编码的期望长度。
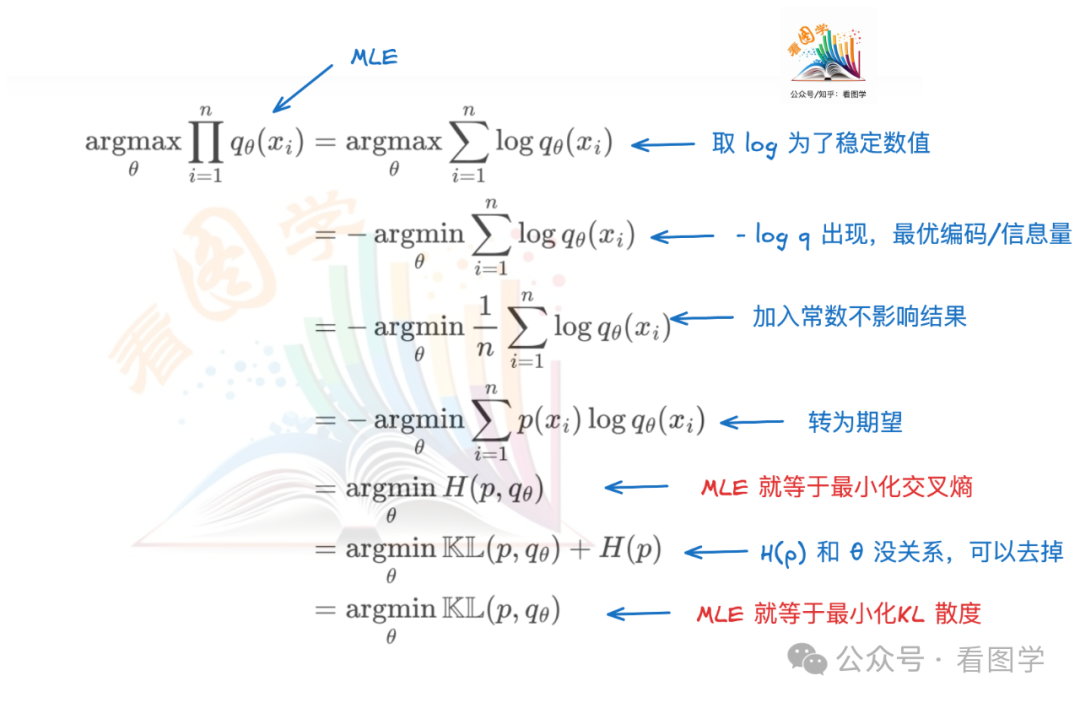
MLE 与 交叉熵
什么是信息量、信息熵、交叉熵与 KL 散度,及其相互之间的关系 https://www.bilibili.com/video/BV1mkgwzZEN9/
Refs
参考资料快照
- https://www.bilibili.com/video/BV1JY411q72n/
- https://zhuanlan.zhihu.com/p/100676922
- https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained
- https://mp.weixin.qq.com/s/T6FONoAFY2cMQGfbCHpFOQ
- https://www.bilibili.com/video/BV1mkgwzZEN9/
- https://blog.csdn.net/sdksdf/article/details/138322038
- https://www.bilibili.com/video/BV1Hw4m117Ka/
- 机器学习笔记 -- 机器学习资源(进行中) | 26 Jul 2025
- MATHEMATICS -- 生成模型数学 —— 概率论基础 | 27 Sep 2024
- MATHEMATICS --《线性代数》奇异值分解(SVD) | 04 Apr 2024
- MATHEMATICS --《概率论与数理统计》宋浩老师(已完成) | 22 Mar 2024
- MATHEMATICS -- 难懂的数学(已完成) | 10 Sep 2022
- MATHEMATICS --《线性代数》宋浩老师(已完成) | 23 Aug 2022
- MATHEMATICS --《高等数学》同济版 宋浩老师(已完成) | 13 Aug 2022
- 机器学习笔记 -- 线性代数 & 微积分 & 概率论与统计学(唐宇迪) | 01 Sep 2020
- 机器学习笔记 -- 环境搭建 & 数学基础 | 29 Aug 2020
 .
.