机器学习笔记 -- 线性代数 & 微积分 & 概率论与统计学（唐宇迪）

Posted on September 1, 2020 (珠海)
机器学习

数学×矩阵的特征值和特征向量

定义

设 $A$ 为 $n \times n$ 阶方阵，若存在常数 $\lambda$ 与 $n$ 维非零列向量 $X$ 使 $AX=\lambda X$ 成立，则称 $\lambda$ 为方阵 $A$ 的特征值，非零向量 $X$ 为 $A$ 的对应于 $\lambda$ 的特征向量。

由 $AX=\lambda X$ → $(A-\lambda E)X=0$。

此方程有非零解的充要条件是：$|A-\lambda E|=0$，即 特征多项式方程 ：

\[\begin{vmatrix} a_{11}-\lambda & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22}-\lambda & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn}-\lambda \end{vmatrix} = 0\]

$P_{A}(\lambda)$ 是高次的多项式，它的求根是很困难的。没有数值方法是通过求它的根来求矩阵的特征值。通常对某个特征值，可以用些针对性的方法来求其近似值。若要求所有的特征值，则可以对 $A$ 做一系列的相似变换，“收敛”到对角阵或上（下）三角阵，从而求得所有特征值的近似。

举例

求矩阵 $A=\left(\begin{array}{rr} 3 & -1 \\ -1 & 3 \end{array}\right)$ 的特征值与特征向量。

解得 $A$ 的两个特征值：$\lambda_1=4$，$\lambda_2=2$。

对应于 $\lambda_1=4$ 的基础解向量：$\vec{P}_{1}=\left(\begin{array}{r}1 \\-1\end{array}\right)$。

对应于 $\lambda_2=2$ 的基础解向量：$\vec{P}_{2}=\left(\begin{array}{r}1 \\1\end{array}\right)$。

乘幂法

幂法是一种迭代法。基本思想：把矩阵的特征值和特征向量作为一个无限序列的极限来求得。求按模最大特征值，即：

\[|\lambda|=\max _{1 \leq i \leq n}\left|\lambda_{i}\right|\]

反幂法

求按模最小特征值，即：

\[|\lambda|=\min _{1 \leq i \leq n}\left|\lambda_{i}\right|\]

雅可比法（Jacobi）

求实对称矩阵所有特征值和特征向量。

3.3-阶数的作用 08:08

泰勒公式（Taylor's formula）是数学分析中的一个重要公式，用于在某一点附近用多项式逼近函数。它以英国数学家 布鲁克 · 泰勒（Brook Taylor） 命名，是 泰勒展开 （Taylor series expansion）的基础。

泰勒公式的表达式

设 $ f(x) $ 在某点 $ x = a $ 处具有足够阶的导数，则可以用泰勒展开式表示它在 $ x $ 附近的近似值： $f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \dots + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n$ 其中：

$ f^{(k)}(a) $ 表示 $ f(x) $ 在 $ x=a $ 处的 第 $ k $ 阶导数 。
$ R_n $ 是 余项（误差项） ，表示截断后剩余的误差。

泰勒余项

常见的泰勒余项形式是 拉格朗日型余项 ： $R_n = \frac{f^{(n+1)}(\xi)}{(n+1)!} (x-a)^{n+1}, \quad \text{ 其中 } \quad \xi \text{ 介于 } a \text{ 和 } x \text{ 之间 }$ 当 $ n \to \infty $ 且 $ R_n \to 0 $ 时，泰勒级数可以无穷展开，并 完全等于 原函数。

常见特殊情况

麦克劳林公式（Maclaurin's formula） 当 $ a=0 $ 时，泰勒公式化为： $f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \dots + \frac{f^{(n)}(0)}{n!}x^n + R_n$ 这被称为 麦克劳林展开 （Maclaurin series）。
常见函数的泰勒展开
- $ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots $
- $ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \dots $
- $ \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \dots $
- $ \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \dots \quad (-1 < x \leq 1) $

应用

函数近似 ：在计算机计算中，泰勒展开用于近似复杂函数，提高计算效率。
极限计算 ：在微积分中，泰勒展开可以用于求解某些极限问题。
微分方程 ：在解微分方程时，泰勒级数提供了一种级数解法。
物理学 ：在物理学中，许多公式（如相对论速度加成公式）可以用泰勒展开进行近似。

3.5-拉格朗日乘子法 09:54

拉格朗日乘子法（Lagrange Multiplier Method） 是一种用于求解 带约束的最优化问题 （即在一定约束条件下找到目标函数的极值）的数学方法。它通过引入一个或多个 拉格朗日乘子（Lagrange Multipliers） 将约束合并到目标函数中，转换为无约束优化问题，从而求解。

问题形式

假设有一个优化问题： $\text{Maximize or Minimize } f(x, y)$ 在约束条件： $g(x, y) = 0$ 下求解。

其中：

$ f(x, y) $ 是 目标函数 （要极大化或极小化的函数）。
$ g(x, y) = 0 $ 是 约束条件 。

拉格朗日函数

为了将约束条件合并到目标函数中，我们引入一个新的变量 $ \lambda $（拉格朗日乘子） ，定义 拉格朗日函数（Lagrange function） ： $\mathcal{L}(x, y, \lambda) = f(x, y) - \lambda g(x, y)$ 然后，我们通过求解 KKT 条件 （一阶必要条件）来找到极值点。

计算步骤

要找到极值点，需要解以下方程组： $\begin{cases} \frac{\partial \mathcal{L}}{\partial x} = f_x - \lambda g_x = 0 \\ \frac{\partial \mathcal{L}}{\partial y} = f_y - \lambda g_y = 0 \\ g(x, y) = 0 \end{cases}$ 其中：

$ f_x, f_y $ 是目标函数的偏导数。
$ g_x, g_y $ 是约束函数的偏导数。
这三条方程联立求解 $ x, y, \lambda $ 的值。

直观理解

拉格朗日乘子法的几何直觉是：

等高线法 ：在约束条件 $ g(x, y) = 0 $ 下，函数 $ f(x, y) $ 的极值点发生在 目标函数等值线与约束曲线相切 的地方。
在这些点上， 目标函数的梯度（$ \nabla f $）与约束函数的梯度（$ \nabla g $）方向相同 ，即： $\nabla f = \lambda \nabla g$ 这说明目标函数在约束条件下不能再沿着约束方向进一步增加或减少。

例子

例子： 求解函数 $ f(x, y) = x^2 + y^2 $ 在约束 $ x + y = 1 $ 下的最小值。

步骤：

定义拉格朗日函数 ： $\mathcal{L}(x, y, \lambda) = x^2 + y^2 - \lambda (x + y - 1)$
求偏导数 ： $\frac{\partial \mathcal{L}}{\partial x} = 2x - \lambda = 0 \quad \Rightarrow \quad \lambda = 2x$ $\frac{\partial \mathcal{L}}{\partial y} = 2y - \lambda = 0 \quad \Rightarrow \quad \lambda = 2y$ $\frac{\partial \mathcal{L}}{\partial \lambda} = x + y - 1 = 0$
联立方程求解 ： $2x = 2y \quad \Rightarrow \quad x = y$ $x + y = 1 \quad \Rightarrow \quad 2x = 1 \quad \Rightarrow \quad x = \frac{1}{2}, y = \frac{1}{2}$
计算最小值 ： $f\left(\frac{1}{2}, \frac{1}{2}\right) = \left(\frac{1}{2}\right)^2 + \left(\frac{1}{2}\right)^2 = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}$

所以， 在 $ x + y = 1 $ 的约束下，$ f(x, y) $ 的最小值是 $ \frac{1}{2} $ ，发生在 $ (x, y) = (\frac{1}{2}, \frac{1}{2}) $ 。

拓展

多个约束条件： 如果有多个约束 $ g_1(x, y) = 0, g_2(x, y) = 0 $，则引入多个拉格朗日乘子 $ \lambda_1, \lambda_2 $ 并构造： $\mathcal{L}(x, y, \lambda_1, \lambda_2) = f(x, y) - \lambda_1 g_1(x, y) - \lambda_2 g_2(x, y)$
不等式约束： 拉格朗日乘子法通常用于 等式约束 ，但可以扩展到 不等式约束 ，形成 KKT（Karush-Kuhn-Tucker）条件 ，用于更一般的最优化问题。

结论

拉格朗日乘子法的核心思想：

通过引入拉格朗日乘子，将 带约束的优化问题 转化为 无约束优化问题 。
目标函数的梯度与约束函数的梯度方向相同（或成比例），即： $\nabla f = \lambda \nabla g$
适用于 等式约束优化 问题，且可以扩展到更复杂的情况（如多个约束或不等式约束）。

这一方法广泛应用于 经济学、物理学、工程优化、机器学习 等领域，例如：

机器学习 中的 拉格朗日对偶（Lagrange Duality） ，用于支持向量机（SVM）。
经济学 中用于 效用最大化问题 。
物理学 中用于 最小作用量原理 。

5.5-SVD 矩阵分解 11:53

SVD（Singular Value Decomposition，奇异值分解）是矩阵分解的一种方法，适用于任何 $ m \times n $ 的实数或复数矩阵。其基本形式是：

\[A = U \Sigma V^T\]

其中：

$ A $ 是 $ m \times n $ 的原始矩阵。
$ U $ 是 $ m \times m $ 的正交矩阵（列向量为左奇异向量）。
$ \Sigma $ 是 $ m \times n $ 的对角矩阵，对角线上的值称为奇异值。
$ V $ 是 $ n \times n $ 的正交矩阵（列向量为右奇异向量）。
$ V^T $ 是 $ V $ 的转置。

主要特性：

降维：SVD 可以用于数据降维，如 PCA（主成分分析）。
矩阵压缩 ：可以通过保留最大的奇异值进行低秩近似，提高计算效率。
求解最小二乘问题 ：用于求解欠定或过定线性方程组。
信号和图像处理 ：在噪声去除、特征提取等方面有广泛应用。

如果 $ A $ 是方阵且满秩，SVD 还可以用于计算矩阵的伪逆、条件数等重要性质。

7.11-马尔科夫不等式 08:36

马尔可夫不等式（Markov's inequality）是概率论中的一个基本不等式，用于估计随机变量取较大值的概率。其数学表达式如下：

设 $X$ 是一个非负的随机变量，且其数学期望 $E[X]$ 存在，则对于任意 $a > 0$，有： $P(X \geq a) \leq \frac{E[X]}{a}$

解释：

该不等式表明：如果一个随机变量的期望较小，那么它取大值的概率也不会太高。
适用于非负随机变量。
这是切比雪夫不等式和其他概率界限推导的基础。

7.12-切比雪夫不等式 11:15

切比雪夫不等式（Chebyshev's Inequality） 描述了随机变量偏离其数学期望的概率上界。具体来说，对于任意随机变量 $ X $ （不一定服从特定分布），如果它的数学期望 $ \mathbb{E}[X] $ 存在，且方差 $ \text{Var}(X) $ 有限，则对于任意 $ k > 0 $，有：

\[P(|X - \mathbb{E}[X]| \geq k\sigma) \leq \frac{1}{k^2}\]

其中，$ \sigma $ 是随机变量的标准差，即 $ \sigma = \sqrt{\text{Var}(X)} $。

直观理解 ：切比雪夫不等式给出了随机变量偏离其均值一定倍数的标准差的概率上限。它适用于任何具有有限方差的分布，即使该分布不是正态分布。例如，当 $ k = 2 $ 时，不等式表明随机变量至少偏离均值 2 倍标准差的概率不会超过 $ 1/4 $，即最多 25%。

应用：

证明大数定律
估计概率分布的尾部行为
处理不服从正态分布的数据分析

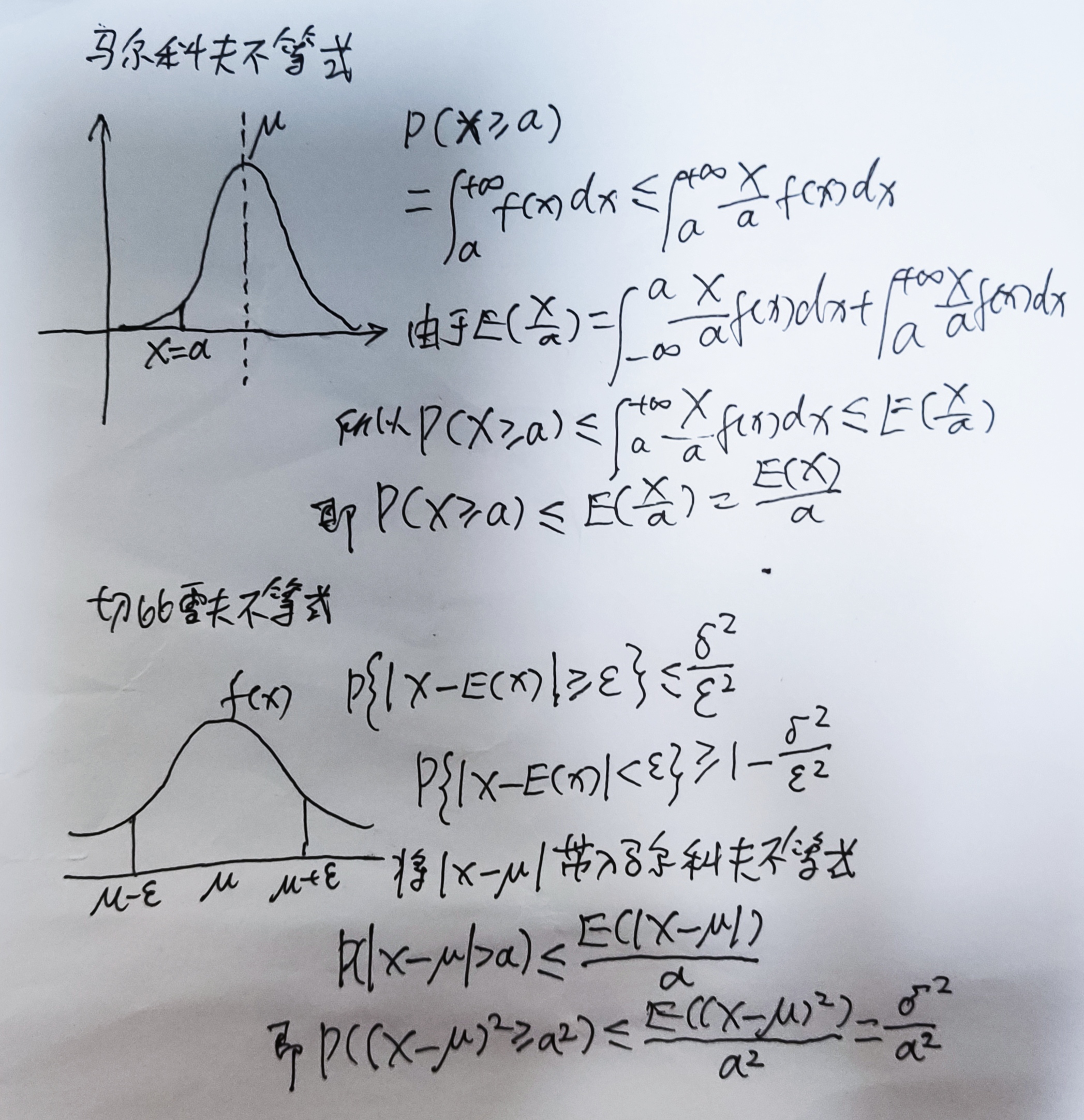
马尔科夫不等式

\[\begin{aligned} & P(X \geqslant a) \\ & =\int_a^{+\infty} f(x) d x \leqslant \int_a^{+\infty} \frac{X}{a} f(x) d x \\ & \text { 由于 } \mathcal{\text { E }}\left(\frac{x}{a}\right)=\int_{-\infty}^{a} \frac{X}{a} f(x) d x+\int_a^{+\infty} \frac{X}{a} f(x) d x \\ & \text { 所以 } P(x \geqslant a) \leqslant \int_a^{+\infty}-\frac{x}{a} f(x) d x \leqslant E\left(\frac{x}{a}\right) \\ & \text { 即 } P(X \geqslant a) \leqslant E\left(\frac{X}{a}\right)=\frac{E(X)}{a} \end{aligned}\]

切比雪夫不等式

\[\begin{aligned} & P\{|X-E(x)| \geqslant \varepsilon\} \leqslant \frac{\delta^2}{\varepsilon^2} \\ & P\{|X-E(x)|<\varepsilon\} \geqslant 1-\frac{\delta^2}{\varepsilon^2} \\ & \text { 将 } \mid x-\mu \mid \text { 带入 } \text { 马尔科夫不等式 } \\ & P(|x-\mu|>\alpha) \leqslant \frac{E(|x-\mu|)}{\alpha} \\ & \text { 即 } P\left((x-\mu)^2 \geqslant a^2\right) \leqslant \frac{E\left((x-\mu)^2\right)}{a^2}=\frac{\sigma^2}{a^2} \end{aligned}\]

https://onlinestatbook.com/stat_sim/sampling_dist/index.html 应用在 n 重贝努里试验中，若已知每次试验事件 A 出现的概率为 0.75，试利用契比雪夫不等式估计 n，使 A 出现的频率在 0.74 至 0.76 之间的概率不小于 0.90。

\[\begin{aligned} &\text { 设在 } n \text { 重贝努里试验中，事件 } A \text { 出现的次数为 } X \text { ，}\\ &\begin{aligned} & \text { 则 } \mathrm{X} \sim b(n, 0.75), \\ & E(X)=n p=0.75 n, D(X)=n p q=0.1875 n, \\ & \begin{aligned} \text { 又 } f_n(A)=\frac{X}{n} \quad \text { 而 } P\left\{0.74<\frac{X}{n}<0.76\right\}=P\{|X-0.75 n|<0.01 n\} \geq 1-\frac{0.1875 n}{(0.01 n)^2} & =1-\frac{1875}{n} \geq 0.90 \\ & \Rightarrow n \geq 18750 \end{aligned} \end{aligned} \end{aligned}\]

7.13-后验概率估计 10:05

7.14-贝叶斯拼写纠错实例 11:47

7.15-垃圾邮件过滤实例 14:10

掷一个硬币，观察到的是“正”，根据最大似然估计的精神，我们应该猜测这枚硬币掷出“正”的概率是 1，因为这个才是能最大化 $P(D|h)$ 的那个猜测。

如果平面上有 N 个点，近似构成一条直线，但绝不精确地位于一条直线上。这时我们既可以用直线来拟合（模型 1）也可以用二阶多项式（模型 2）拟合，也可以用三阶多项式（模型 3），特别地，用 N-1 阶多项式便能够保证肯定能完美通过 N 个数据点。那么，这些可能的模型之中到底哪个是最靠谱的呢？ 奥卡姆剃刀：越是高阶的多项式越是不常见。

8-1-正太分布 19:23
8-2-二项式分布 11:03
8-3-泊松分布 15:56
8-4-均匀分布 03:23
8-5-卡方分布 05:36
8-6-beta 分布 14:55

9-5-高斯核函数 08:51

11-5-回归方程求解小例子 06:33

https://scikit-learn.org.cn/lists/2.html https://scikit-learn.cn/stable/

分类标识对象所属的类别。应用范围：垃圾邮件检测，图像识别。算法：SVM 最近邻随机森林更多 …

回归预测与对象关联的连续值属性。应用范围：药物反应，股票价格。算法：SVR 最近邻随机森林更多 …

聚类自动将相似对象归为一组。应用：客户细分，分组实验成果。算法：K-均值谱聚类 MeanShift 更多 …

降维减少要考虑的随机变量的数量。应用：可视化，提高效率。算法：K-均值特征选择非负矩阵分解更多 …

模型选择 比较，验证和选择参数和模型。应用：通过参数调整改进精度。算法：网格搜索交叉验证指标更多 …

预处理 特征提取和归一化。应用程序：转换输入数据，例如文本，以供机器学习算法使用。算法：预处理特征提取更多 …

有监督学习 1.1 线性模型 1.2 线性和二次判别分析 1.3 内核岭回归 1.4 支持向量机 1.5 随机梯度下降 1.6 最近邻 1.7 高斯过程 1.8 交叉分解 1.9 朴素贝叶斯 1.10 决策树 1.11 集成算法 1.12 多类和多标签算法 1.13 特征选择 1.14 半监督学习 1.15 Isotonic 回归 1.16 概率校准 1.17 神经网络模型（有监督）
无监督学习 2.1. 高斯混合模型 2.2. 流形学习 2.3. 聚类 2.4. 双聚类 2.5. 分解成分中的信号（矩阵分解问题） 2.6. 协方差估计 2.7. 奇异值和异常值检测 2.8. 密度估计 2.9. 神经网络模型（无监督）
模型选择与评估 3.1 交叉验证：评估模型表现 3.2 调整估计器的超参数 3.3 指标和评分：量化预测的质量 3.4 模型持久性 3.5 验证曲线：绘制分数以评估模型
检验 4.1 部分依赖图 4.2 基于排列的特征重要性
可视化 5.1 提供的绘图工具
数据集转换 6.1 管道和复合估算器 6.2 特征提取 6.3 数据预处理 6.4 缺失值插补 6.5 无监督降维 6.6 随机投影 6.7 内核近似 6.8 成对度量，近似关系和内核 6.9 转换预测目标（y）
数据集加载实用程序 7 数据集加载工具
使用 scikit-learn 计算 8.1. 大数据的计算策略 8.2. 计算性能 8.3. 并行，资源管理和配置

Missing data visualization module for Python. https://github.com/ResidentMario/missingno

12-3-Z 检验基本原理 07:04

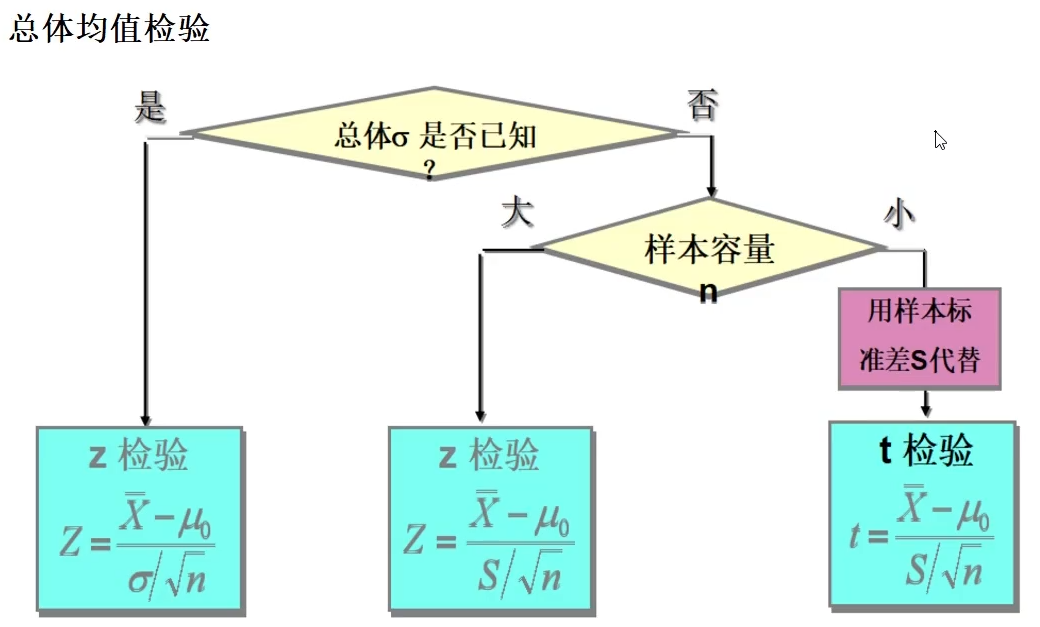
12-10-Python 假设检验实例 12:35

12-11-Python 卡方检验实例 08:00

13-1-相关分析概述 09:04

13-2-皮尔森相关系数 08:17

皮尔森相关系数（ Pearson correlation coefficient ），简称 皮尔森系数 ，是衡量两个变量之间线性关系强度和方向的统计指标。

13-4-斯皮尔曼等级相关 14:07

斯皮尔曼等级相关（Spearman’s rank correlation coefficient，简称 Spearman ρ）是一种非参数统计方法，用来衡量两个变量之间的单调关系强度和方向。

方法	数据类型	假设条件	衡量关系类型	对异常值敏感性	典型用途
皮尔逊相关 (Pearson’s r)	连续型（区间 / 比例尺度）	两变量近似正态分布，线性关系，方差齐性	线性关系强度与方向	高（异常值会显著影响 r 值）	连续变量之间的线性相关，如身高与体重
斯皮尔曼等级相关 (Spearman’s ρ)	连续型或有序型（ordinal）	无需正态分布，只要求单调关系	单调关系（线性或非线性）	低（秩次减少异常值影响）	排名数据、非正态分布数据、有离群点的数据
肯德尔相关 (Kendall’s τ)	有序型（ordinal）	无需正态分布	单调关系，基于一致对和不一致对的比例	很低（比斯皮尔曼更稳健）	样本量较小、排名有大量并列时
点双列相关 (Point-biserial)	一连续型 + 一二分变量	连续变量正态分布	类似皮尔逊，但针对二分 + 连续	高	性别（二分）与测试成绩（连续）的关系
Phi 系数 (Φ)	两个二分变量	无需正态分布	二分变量的关联程度	中等	性别与是否及格等二分变量关系
Cramer’s V	分类变量	无需正态分布	多分类变量的关联强度	中等	分类数据（名义变量）关系，如职业类别与消费偏好
偏相关 (Partial correlation)	连续型	同 Pearson 条件	控制其他变量后剩余的线性关系	高	多变量分析中控制混杂因素
典型相关 (Canonical correlation)	两组连续型变量	正态性、线性	两组变量间的总体线性关系	高	多维变量组之间的关系

规则是最好覆盖长尾问题，相反模型要解决长尾问题更难，只是规则遇到长尾直接卡壳，模型可能会懵一个。规则可解释，安全性容易验证。

13-5-肯德尔系数 06:49

13-6-质量相关分析 13:34

13-7-偏相关与复相关 07:35

14-1-方差分析概述 06:49

总变异（总平方和，SST）：样本数据的整体波动程度。
组间变异（组间平方和，SSA）：不同组均值之间的差异，反映因素效应。
组内变异（组内平方和，SSE）：同一组内样本的变异，反映随机误差。

方差分析通过比较“组间变异”与“组内变异”的大小关系，来判断组均值是否显著不同。

14-2-方差的比较 11:51

14-3-方差分析计算方法 14:01

14-4-方差分析中的多重比较 08:16

14-5-多因素方差分析 09:26

14-6-Python 方差分析实例 08:35

15-1-1-层次聚类概述 04:42

层次聚类（Hierarchical Clustering）中，计算两类（簇）之间距离的方法主要有三种经典方式，分别是：

1. 单链接法（Single Linkage）

定义：两类中距离最近的两个样本点之间的距离。
计算方式 ：
\[d(A, B) = \min_{a \in A, b \in B} d(a, b)\]
特点：倾向形成链状簇，容易产生“链式效应”，对噪声敏感。

2. 全链接法（Complete Linkage）

定义：两类中距离最远的两个样本点之间的距离。
计算方式 ：
\[d(A, B) = \max_{a \in A, b \in B} d(a, b)\]
特点：聚类形状更紧凑，避免链式效应，但对异常点敏感。

3. 平均链接法（Average Linkage）

定义：两类中所有样本点两两距离的平均值。
计算方式 ：
\[d(A, B) = \frac{1}{|A||B|} \sum_{a \in A} \sum_{b \in B} d(a, b)\]
特点：折中方法，平衡了单链接和全链接的缺点，效果通常较好。

15-1-2-层次聚类流程 12:11

15-1-3-层次聚类实例 11:34

15-2-1-KMEANS 算法概述 11:34

15-2-2-KMEANS 工作流程 09:43

15-2-3-KMEANS 迭代可视化展示 08:20

15-3-1-DBSCAN 聚类算法 11:04

15-3-2-DBSCAN 工作流程 15:04

劣势

高维数据有些困难（可以做降维）
参数难以选择（参数对结果的影响非常大）
Sklearn 中效率很慢（数据削减策略）

15-3-3-DBSCAN 可视化展示 08:53

15-4-1-多种聚类算法概述 04:35

15-4-2-聚类案例实战 17:20

聚类评估：轮廓系数 Silhouette Coefficient

16-1-贝叶斯分析概述 07:22

16-2-概率的解释 06:07

16-3-贝叶斯学派与经典统计学派的争论 05:50

16-4-贝叶斯算法概述 06:59

正向概率 vs 逆向概率。

“最大似然 vs 最大后验 (MAP)” 模型比较的基本理论

最大似然 (Maximum Likelihood, ML)
- 核心思想：选择 最符合观测数据 的模型，即使观测数据出现的概率 $P(D|h)$ 最大的假设 $h$。
- 例子：
  - 掷一次硬币，观测结果是“正”。
  - 根据最大似然估计，最能解释这个观测数据的模型是“这枚硬币正面朝上的概率 = 1”。
  - 因为在 $p=1$ 的情况下，观测结果“正”的概率最大化。
奥卡姆剃刀 (Occam's Razor)
- 核心思想：在解释数据时， 更简单或先验概率 $P(h)$ 较大的模型更有优势 。
- 含义：即使某个复杂模型能更好地拟合当前数据，也不一定比简单模型更优，因为过度复杂的模型可能缺乏泛化能力。