图形学笔记 -- GAMES101: 现代计算机图形学入门（光线追踪和动画）

• https://mathpix.com/
• GAMES101: 现代计算机图形学入门
• GAMES202: 高质量实时渲染
• GAMES101-现代计算机图形学入门-闫令琪

十三、光线追踪（基本原理）Ray Tracing

• Whitted-Style Ray Tracing

Why Ray Tracing?

Light Rays Three ideas about light rays

1. Light travels in straight lines (though this is wrong) 直线
2. Light rays do not “collide” with each other if they cross (though this is still wrong) 不碰撞
3. Light rays travel from the light sources to the eye (but the physics is invariant under path reversal - reciprocity). 可逆性

“And if you gaze long into an abyss, the abyss also gazes into you.” — Friedrich Wilhelm Nietzsche (translated)

求射线和一个平面的交点？一个重心坐标，搞定，真的是神奇哦。

Möller Trumbore Algorithm

Axis-Aligned Bounding Box (AABB) （轴对齐包围盒）

• The ray enters the box only when it enters all pairs of slabs
• The ray exits the box as long as it exits any pair of slabs
• For the 3D box, tenter = max{tmin}, texit = min{tmax}

十四、光线追踪（加速结构）

Uniform Spatial Partitions (Grids)

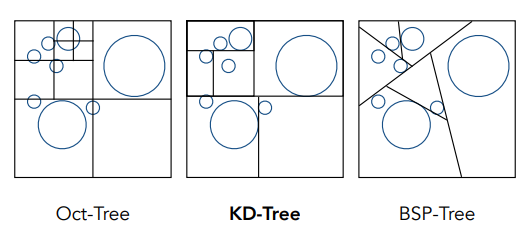
Spatial Partitioning Examples

Data Structure for KD-Trees

Internal nodes store

• split axis: x-, y-, or z-axis
• split position: coordinate of split plane along axis
• children: pointers to child nodes
• No objects are stored in internal nodes Leaf nodes store
• list of objects

Bounding Volume Hierarchy (BVH) 快速选择算法 其时间复杂度可以达到 \(O(n)\)。 网页里面的代码存在 bug，稍微改了改。^_^

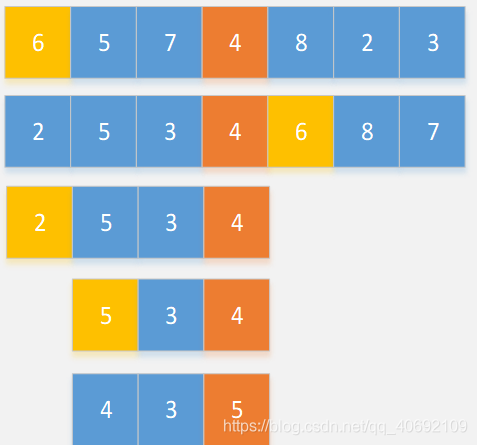
#include "stdafx.h"
#include <assert.h>

template<typename T>
void qSwap(T arr[], int x, int y) {
    if (x == y) return;
    T temp = arr[x];
    arr[x] = arr[y];
    arr[y] = temp;
}

template<typename T>
void qDebug(T arr[], int low, int high, int k, int size) {
    printf("%d %d %d - ", low, high, k);
    for (int i = 0; i < size; i++) {
        printf(i == low ? "[" : " ");
        printf("%d", arr[i]);
        printf(i == high ? "]" : " ");
    }
    printf("\n");
}

// 在选出第 K 大的元素之后，我们也自然有了前 K 大的数，
// 因为在 K 右边的数都是比 K 大的，在 K 左边的数都是比 K 小的。
template<typename T>
T qSelect(T arr[], int low, int high, int k, int size) {
    qDebug(arr, low, high, k, size);
    if (low >= high) {
        assert(k == low); // 断言断的是我们的代码没有 bug。
        return arr[low];
    }
    int left = low;
    int right = high + 1;
    int key = arr[low];
    while (true) {
        /* 从左向右找比 key 大的值 */
        while (arr[++left] < key) {
            if (left == high) {
                break;
            }
        }
        /* 从右向左找比 key 小的值 */
        while (arr[--right] > key) {
            if (right == low) {
                break;
            }
        }
        if (left >= right) break;
        /* 交换 left, right 对应的值 */
        qSwap(arr, left, right);
    }
    /* 中枢值与 right 对应值交换 */
    assert(arr[right] <= key);
    // 左边都是比 key 小等的，右边都是比 key 大等的。
    qSwap(arr, low, right);
    // 从小到大排序的第 k 个元素。
    if (right > k) {
        return qSelect(arr, low, right - 1, k, size);
    }
    else if (right < k) {
        return qSelect(arr, right + 1, high, k, size);
    }
    else {
        return arr[right];
    }
}

int compare(const void* a, const void* b) {
    return (*(int*)a - *(int*)b);
}

int* genArray(int size) {
    int* ali = new int[size];
    for (int i = 0; i < size; i++) {
        ali[i] = abs(rand()) % 10;
    }
    return ali;
}

void freeArray(int* ali) {
    delete[] ali;
}

int maintest() {
    int size = abs(rand()) % 8 + 1;
    int* ali = genArray(size);

    int k = abs(rand()) % size;
    int result = qSelect(ali, 0, size - 1, k, size);
    qsort(ali, size, sizeof(int), compare);
    if (result != ali[k]) {
        assert(result == ali[k]);
    }
    freeArray(ali);
    printf("result - %d \n", result);
    return 0;
}

int _tmain(int argc, _TCHAR* argv[])
{
    for (int i = 0; i < 10000; i++) {
        maintest();
    }
    return 0;
}

跑出来的示例：

0 1 0 - [7  4]
0 0 0 - [4] 7
result - 4
0 1 0 - [4  8]
result - 4
0 2 1 - [4  5  5]
1 2 1 -  4 [5  5]
1 1 1 -  4 [5] 5
result - 5
0 3 3 - [1  1  5  2]
2 3 3 -  1  1 [5  2]
result - 5
0 4 2 - [1  4  2  3  2]
1 4 2 -  1 [4  2  3  2]
1 3 2 -  1 [2  2  3] 4
result - 2
0 5 0 - [6  8  5  7  6  1]
0 2 0 - [6  1  5] 6  7  8
0 1 0 - [5  1] 6  6  7  8
0 0 0 - [1] 5  6  6  7  8
result - 1
0 5 3 - [2  7  9  5  4  3]
1 5 3 -  2 [7  9  5  4  3]
1 3 3 -  2 [4  3  5] 7  9
3 3 3 -  2  3  4 [5] 7  9
result - 5
0 2 0 - [3  3  4]
0 0 0 - [3] 3  4
result - 3
0 7 3 - [3  8  7  4  2  7  7  9]
2 7 3 -  2  3 [7  4  8  7  7  9]
2 4 3 -  2  3 [7  4  7] 7  8  9
2 3 3 -  2  3 [7  4] 7  7  8  9
result - 7
0 5 0 - [9  8  6  5  0  2]
0 4 0 - [2  8  6  5  0] 9
0 0 0 - [0] 2  6  5  8  9
result - 0

BVH Traversal

Intersect(Ray ray, BVH node) {
    if (ray misses node.bbox) return;
    if (node is a leaf node)
        test intersection with all objs;
        return closest intersection;
    hit1 = Intersect(ray, node.child1);
    hit2 = Intersect(ray, node.child2);
    return the closer of hit1, hit2;
}

Spatial vs Object Partitions

Spatial partition (e.g.KD-tree)

• Partition space into non-overlapping regions 区域不交叠
• An object can be contained in multiple regions 一个物体可能在多个区域

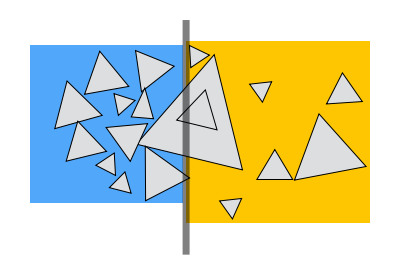
Object partition (e.g. BVH)

• Partition set of objects into disjoint subsets 根据物体分割
• Bounding boxes for each set may overlap in space 区域可能存在交叠

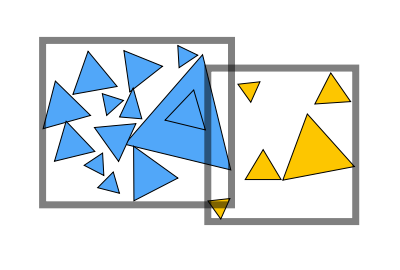
Whitted-Style 光线追踪算讲完了。

Basic radiometry（辐射度量学）

Advertisement: new topics from now on, scarcely covered in other graphics courses

• Radiant Flux 辐射通量 ? Radiant Energy and Flux (Power)

Definition: Radiant energy is the energy of electromagnetic radiation. It is measured in units of joules, and denoted by the symbol:

Definition: Radiant flux (power) is the energy emitted, reflected, transmitted or received, per unit time.

功率 ?

• Radiant Intensity 辐射强度 ? “Radiant Intensity” 发射出去多少光线。

• Irradiance 辐 [射] 照度 ? “Irradiance” 接收到多少光线。

• Radiance 辐 [射] 亮度 ? “Radiance” 传播过程中的度量。

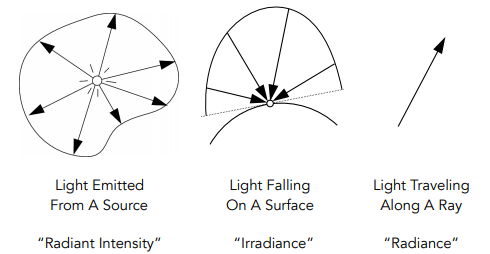
Important Light Measurements of Interest

十五、光线追踪（辐射度量学、渲染方程与全局光照）

辐射通量：单位立体角内的辐射通量

Radiant energy (barely used in CG)

• the energy of electromagnetic radiation \(Q[\mathrm{~J}=\text { Joule }]\)

Radiant flux (power)

• Energy per unit time \(\Phi \equiv \frac{\mathrm{d} Q}{\mathrm{~d} t}[\mathrm{~W}=\text { Watt }][\operatorname{lm}=\text { lumen }]\)

Radiant intensity

• power per unit solid angle \(I(\omega) \equiv \frac{\mathrm{d} \Phi}{\mathrm{d} \omega}\)

Solid Angle

• ratio of subtended area on sphere to radius squared \(\Omega=\frac{A}{r^{2}}\)

Irradiance

Definition: The irradiance is the power per unit area incident on a surface point. 辐照度：单位面积上的辐射通量

Radiance

Radiance is the fundamental field quantity that describes the distribution of light in an environment

• Radiance is the quantity associated with a ray
• Rendering is all about computing radiance

Definition: The radiance (luminance) is the power emitted, reflected, transmitted or received by a surface, per unit solid angle, per projected unit area.

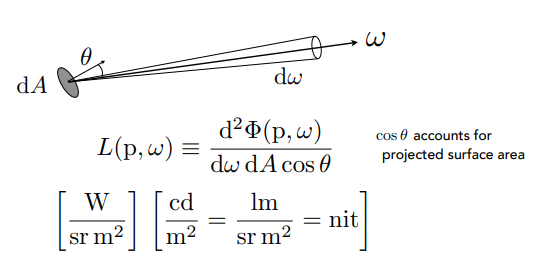
Bidirectional Reflectance Distribution Function (BRDF)

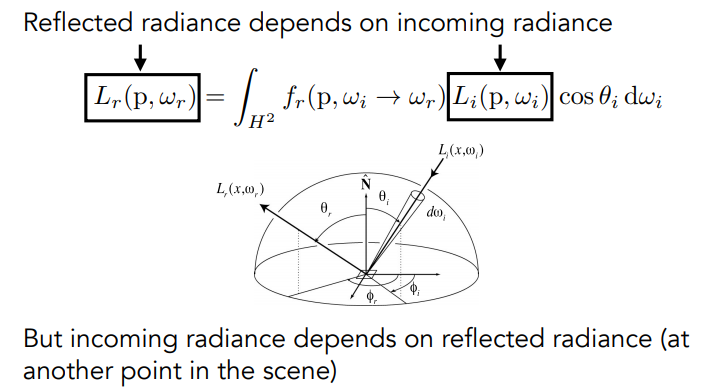
The Reflection Equation: Recursive Equation

概率： Continuous Case: Probability Distribution Function (PDF)

Conditions on p(x): \(p(x) \geq 0 \text { and } \int p(x) d x=1\)

Expected value of X: \(E[X]=\int x p(x) d x\)

十六、光线追踪（蒙特卡洛积分与路径追踪）

Monte Carlo estimator 基本蒙特卡洛估计器

十七、材质与外观

Material == BRDF BRDF 的全名是 bidirectional reflectance distribution function

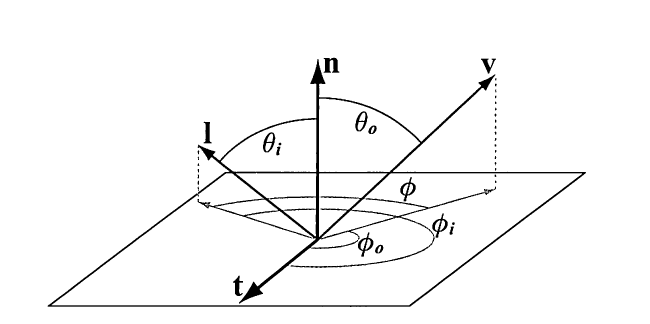
十八、高级光线传播与复杂外观建模

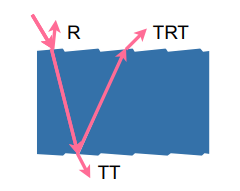
毛发渲染模型 Marschner model

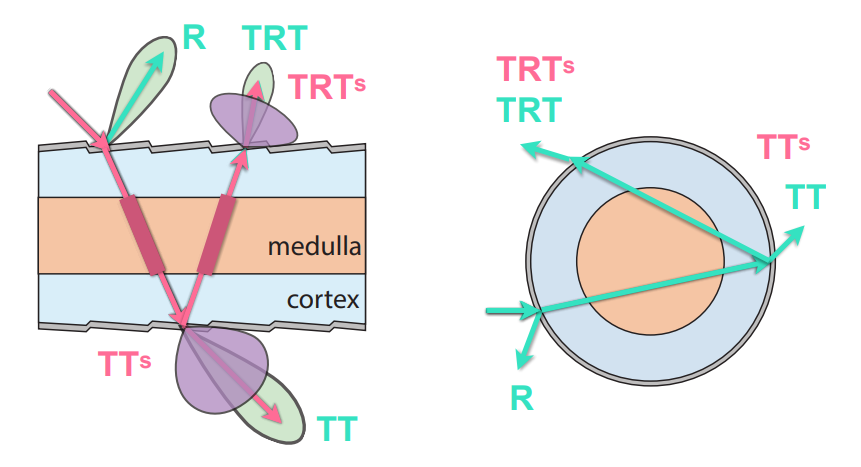
Double Cylinder Model — Lobes

相机与透镜

摄影入门，相机与透镜 的图形学原理。根据 闫令琪 课程整理。 照相机与透镜（光圈、快门和景深）

• Can reconstruct every possible view, at every moment, from every position, at every wavelength
• Contains every photograph, every movie, everything that anyone has ever seen! it completely captures our visual reality! Not bad for a fXncWion«

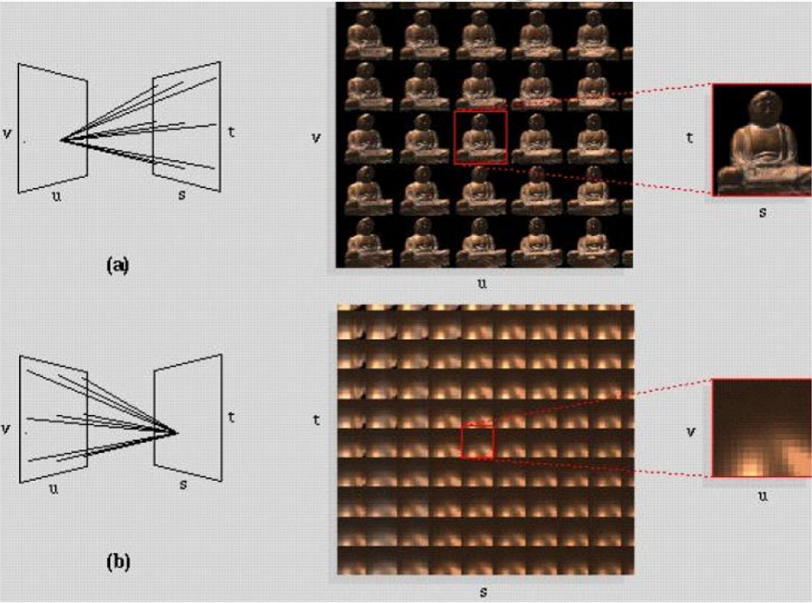
Lumigraph / Lightfield

光场、颜色与感知 Color and Perception

各种颜色空间是怎么推导来的？

400 纳米到 700 纳米。

What is Color?

• Color is a phenomenon of human perception; it is not a universal property of light
• Different wavelengths of light are not “colors”

动画与模拟（基本概念、质点弹簧系统、运动学）

Introduction to Computer Animation

• History
• Keyframe animation
• Physical simulation
• Kinematics
• Rigging

• Film: 24 frames per second • Video (in general): 30 fps • Virtual reality: 90 fps

逆运动学，采用梯度下降算法求解。

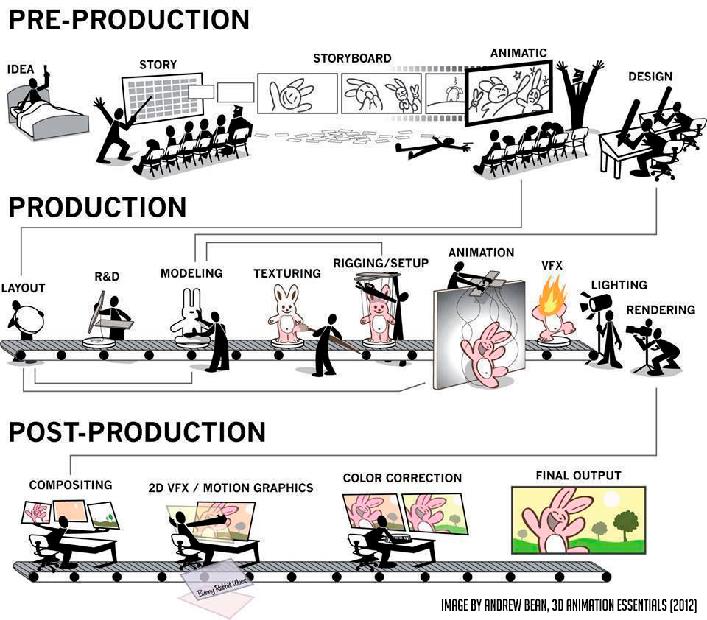
The Production Pipeline

动画与模拟（求解常微分方程，刚体与流体）

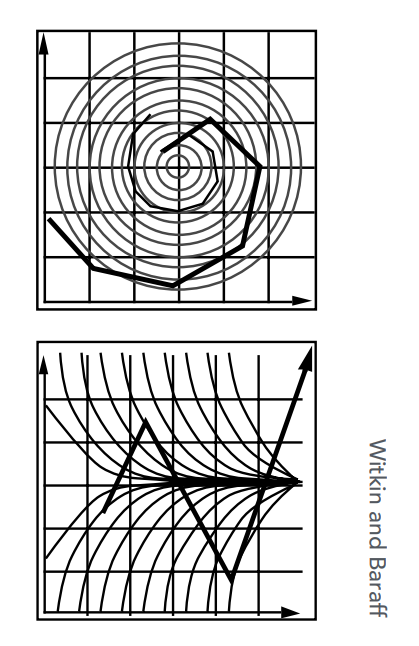
Instability of the Euler Method

Some Methods to Combat Instability

• Midpoint method / Modified Euler
  • Average velocities at start and endpoint
  • 采用中间的速度。
• Adaptive step size
  • Compare one step and two half-steps, recursively, until error is acceptable
  • 不断细分，直到误差小于一个特定值。
• Implicit methods
  • Use the velocity at the next time step (hard)
  • Implicit Euler Method
• Position-based / Verlet integration – Verlet 积分法
  • Constrain positions and velocities of particles after time step

Runge-Kutta Families

Runge-Kutta Families

This paper simplified the mass-spring model using the rigid stick to replace the spring connection of masses, and using the Verlet integration to calculate the position and speed of the mass. 在质点-弹簧模型的基础上，对织物模型进行进一步的简化。将连接质点的弹簧换成了刚性杆，同时采用 Verlet 积分法计算质点的位置和速度。

Rigid Body Simulation 刚体模拟

Fluid Simulation

Taichi 语言基础 刚体 液体 烟雾 弹塑性体 PIC/FLIP 法 Krylov-子空间求解器 预条件 无矩阵法 多重网格 弱形式与有限元 隐式积分器 辛积分器 拓扑优化 带符号距离场 自由表面追踪 物质点法 大规模物理效果渲染 现代处理器微架构 内存层级 并行编程 GPU 编程 稀疏数据结构 可微编程…

• https://mathpix.com/
• https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
• https://sites.cs.ucsb.edu/~lingqi/teaching/games202.html
• https://www.bilibili.com/video/BV1X7411F744
• https://blog.csdn.net/qq_40692109/article/details/102696615