图形学笔记 -- OpenGL 图形学 / 视差贴图(Parallax Mapping)
作为实现 Bump Mapping(凹凸映射) 的技术之一,Parallax Mapping(视差映射)的目的同样也是让平坦表面实现凹凸效果。 和 Normal Mapping 相比,Parallax Mapping 能实现更加真实和强烈的凹凸感。

Vulkan_ 法线映射、视差映射、陡视差映射和视差遮挡映射 
Parallax Mapped

需要说明的是我们在分析视差贴图的时候使用的是切线空间,这和法线贴图是一样的,切线空间中的切线和副切线是与纹理坐标 $uv$ 对齐的, 上图中只显示了 $u$ 方向上的情况,在 $v$ 方向上是一样的。
当前实际的落点是点 $b$,$u$ 坐标是 $ub$,而理想的落点是在点 $a$,$u$ 坐标是 $ua$。 如果能有一个 $delta$ 量,把 $ub$ 加上 $delta$ 等于 $ua$,似乎就可以了。
但是还有个问题是,因为视线的方向是一直在变化的,这就导致了 $delta$ 量不可能是一个固定的值。 所以暂且没有什么好的办法求出 $delta$,那么就把问题想简单点。 这里不要求精确的 $delta$,只要近似的就可以。于是有了一张称为高度图的纹理,它存储了点 $b$ 在切线空间的真实凹凸表面的凹陷或凸起程度。 黑色($0$)表示不凸起,白色($1$)表示完全凸起。我们可以试着使用这个值来最大可能的近似模拟出 $delta$ 值。
// 计算 uv 的偏移 delta
inline float2 ParallaxUvDelta(v2f i)
{
// 高度图中描述的高度数据
half h = tex2D(_ParallaxMap, i.uvMain).r;
// 切线空间中的视线方向
float3 viewDir = normalize(i.viewDir);
// 将三维的视线向量投影到二维的 uv 平面,乘以高度数据
// _ParallaxScale 是一个用户可调节的值,根据效果需要进行调节,数值太大造成视觉上的严重错误
float2 delta = viewDir.xy / viewDir.z * h * _ParallaxScale;
return delta;
}
float2 uvDelta = ParallaxUvDelta(i);
i.uvMain += uvDelta;
i.uvBump += uvDelta;
需要把世界坐标下的观察矢量变换到切空间下,因此对每个顶点来说都要一个切空间坐标变换矩阵。 在 parallax mapping 中,我们将用纹理坐标对高度图进行查找,根据所得结果对自身进行修改,最后再进行普通的纹理查找。 看代码才看明白,这个计算过程是反过来的:

Parallax Mapping 的思想
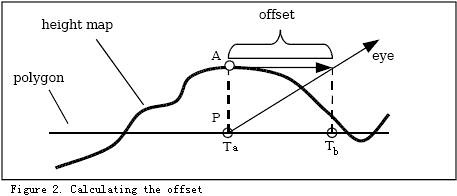
Parallax Mapping 的算法

其中,Irrlicht GLSL2 里面的实现:
uniform vec3 uEyePosition; // 相机坐标
varying vec3 vEyeVector; // 相机向量
void main()
{
vec3 EyeVector = uEyePosition - inVertexPosition;
vEyeVector.x = dot(inVertexTangent, EyeVector);
vEyeVector.y = dot(inVertexBinormal, EyeVector);
vEyeVector.z = dot(inVertexNormal, EyeVector);
vEyeVector *= vec3(1.0, -1.0, -1.0);
}
uniform float uFactor; // 纹理颜色的乘积参数
varying vec3 vEyeVector; // 相机向量
void main()
{
vec4 TempFetch = texture2D(uTextureUnit1, vTexCoord) * 2.0 - 1.0;
TempFetch *= uFactor;
vec3 EyeVector = normalize(vEyeVector);
vec2 TexCoord = EyeVector.xy * TempFetch.w + vTexCoord;
// vec4 Color = texture2D(uTextureUnit0, vTexCoord);
vec4 Color = texture2D(uTextureUnit0, TexCoord);
// vec3 Normal = texture2D(uTextureUnit1, vTexCoord).xyz * 2.0 - 1.0;
vec3 Normal = texture2D(uTextureUnit1, TexCoord).xyz * 2.0 - 1.0;
}
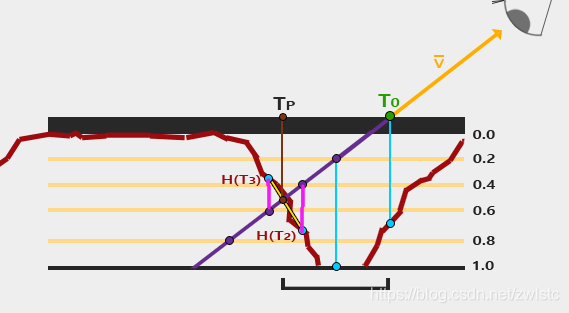
Steep Parallax Mapped

用等分线给分层采样。然后根据红点蓝点的规律,最后插值找到相对准确的结果。
陡峭视差映射 Steep Parallax Mapping / 视差遮蔽映射 Parallax Occlusion mapping
inline float2 ParallaxUvDelta(Input i)
{
float3 viewDir = normalize(i.viewDir);
// 细分的层数
const float numLayers = 20;
// 单层步进的高度
float layerHeight = 1.0 / numLayers;
// 最高的高度值
float currentLayerHeight = 1.0;
// delta 最大值
float2 P = viewDir.xy * _ParallaxScale;
// delta 单步逼近值
float2 deltaTexCoords = P / numLayers;
// 开始一步步逼近,直到找到合适的红点
float2 currentTexCoords = i.uv_MainTex;
float currentDepthMapValue = tex2D(_ParallaxMap, currentTexCoords).r;
while (currentLayerHeight > currentDepthMapValue)
{
currentTexCoords -= deltaTexCoords;
currentDepthMapValue = tex2D(_ParallaxMap, currentTexCoords).r;
currentLayerHeight -= layerHeight;
}
// 计算 h1 和 h2
float2 prevTexCoords = currentTexCoords + deltaTexCoords;
float afterHeight = currentDepthMapValue - currentLayerHeight;
float beforeHeight = currentLayerHeight + layerHeight - tex2D(_ParallaxMap, prevTexCoords).r;
// 利用 h1 h2 得到权重,在两个红点间使用权重进行差值
float weight = afterHeight / (afterHeight + beforeHeight);
float2 finalTexCoords = prevTexCoords * weight + currentTexCoords * (1.0 - weight);
return finalTexCoords - i.uv_MainTex;
}
float2 uvDelta = ParallaxUvDelta(i);
i.uvMain += uvDelta;
i.uvBump += uvDelta;
历史
1978 年的时候,大神 James Blinn(就是那位优化了 Phong 光照模型,将其改为 Blinn-Phong 的牛人) 在 "Simulation of Wrinkled Surfaces" 中提出了凹凸贴图(Bump mapping)。
而到了 1996 年,法线贴图(Normal Mapping)作为凹凸贴图的一种实现产生了, 由 Venkat Krishnamurthy and Marc Levoy 在 Fitting Smooth Surfaces to Dense Polygon Meshes 中提出。
时间来到 2001 年,Tomomichi Kaneko et al(这个 et al 是拉丁文,代表其他人,也就是说这个技术不是他一个人搞出来的)在 Detailed Shape Representation with Parallax Mapping 提出了称得上是加强版的法线贴图技术,视差贴图。
4 年后,又有人在 Real-time relief mapping on arbitrary polygonal surfaces 一文中提出了终极加强版,浮雕贴图。
维护一个 3D 引擎工作量非常大,因为硬件在不断升级,算法也在不断升级。

parallax mapping

steep parallax mapping

steep parallax mapping 线性插值
需要基于物理的渲染
Physically Based Rendering。 基于物理材质是以后游戏开发的一个趋势,所以我们有必要从现在就开始逐步把制作思路从原来的模拟光照转变为现在物理真实的光照。
近来,基于物理的渲染(PBR)是一项令人激动的实时渲染的趋势。 这个术语包含了很多内容,通常会让人产生困惑,以至于不明白它到底是什么。
基于物理的渲染系统不同于以往的渲染系统,大部分更细节的原因是关于光和表面的行为。 着色能力有了很大的进步,一些老旧的近似模拟的效果和制作方法可以抛弃了。
Refs
- [1] 视差贴图(Parallax Mapping)ref

- [2] Jim's GameDev Blog
- [3] 视差贴图(Parallax Mapping)与陡峭视差贴图 (Steep Palallax Mapping)

- [4] 视差角度遮挡贴图
- [5] 视差贴图 (parallax mapping) 学习笔记
- [6] 视差贴图(Parallax Mapping)以及浮雕贴图(Relief Mapping)在 Unity 中的实现

参考资料快照
- https://chengkehan.github.io/ParallaxMapping.html
- https://www.cnblogs.com/jim-game-dev/p/5410529.html
- https://blog.csdn.net/happykocola/article/details/72812081
- https://blog.csdn.net/soilwork/article/details/1452437
- https://blog.csdn.net/qq_35312463/article/details/106980557
- https://chengkehan.github.io/WhyWeNeedPBR.html
- https://chengkehan.github.io/PhysicallyBasedShading1.html
- https://chengkehan.github.io/PhysicallyBasedShading2.html
- https://chengkehan.github.io/MyPBR.html
- https://chengkehan.github.io/LearningPBR.html
- https://blog.csdn.net/weixin_30920091/article/details/96251306
- https://chengkehan.github.io/
- https://blog.csdn.net/xiaoge132/article/details/51173002
- https://docs.unrealengine.com/udk/Three/DevelopmentKitGemsParallaxOccludedMappingCH.html
- https://gameinstitute.qq.com/community/detail/124840
- https://www.jianshu.com/p/edf6589122b2
- 图形学笔记 -- OpenGL 图形学 / 视差贴图(Parallax Mapping) | 07 Jan 2021
- 图形学笔记 -- OpenGL 图形学 / 高级光照 阴影 shadowMapping | 24 Dec 2020
- 图形学笔记 -- LearnOpenGL CN 学习笔记(原书复习) | 21 Dec 2020
- 图形学笔记 -- OpenGL 图形学 / 高级 OpenGL:Stencil Test(模板测试) | 16 Dec 2020
- 图形学笔记 -- OpenGL 图形学 / 高级 OpenGL:深度测试、面剔除、帧缓冲 等 | 15 Dec 2020
- 图形学笔记 -- OpenGL 图形学 / 高级光照 Blinn-Phong & 阴影 | 14 Dec 2020
- 图形学笔记 -- OpenGL 图形学 / 模型加载 | 11 Dec 2020
- 图形学笔记 -- OpenGL 图形学 / 坐标系统 | 11 Dec 2020
- 图形学笔记 -- OpenGL 图形学 / 冯氏光照模型 | 09 Dec 2020
- 图形学笔记 -- 计算机图形学 OPENGL 入门 | 11 Nov 2020
 .
.