图像处理笔记 -- 傅里叶变换

Posted on September 26, 2020 (珠海)
图像处理

数学推导傅里叶级数与傅里叶变换

傅里叶分析之掐死教程 https://zhuanlan.zhihu.com/p/19763358

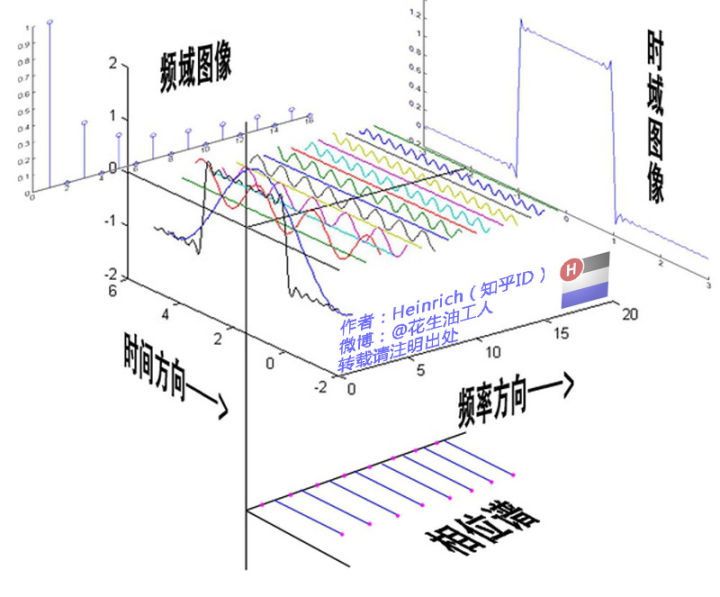
Part1. 三角函数的正交性 https://www.bilibili.com/video/BV1Et411R78v

Part2. 周期为 $2\varPi$ 的函数展开 https://www.bilibili.com/video/BV17t411d7hm

Part3. 周期为 $2L$ 的函数展开 https://www.bilibili.com/video/BV1wb411K7Kp

Part4. 傅里叶级数的复数形式 https://www.bilibili.com/video/BV13b411P7mU

Part5. 从傅里叶级数推导傅里叶变换 https://www.bilibili.com/video/BV1jt411U7Bp

Part6. 总结与闲话 https://www.bilibili.com/video/BV1St41117fH

“珂学原理”No. 26“拉普拉斯变换了什么？”

复数的物理意义

复数的物理意义是什么？

转载文章：傅里叶变换分析之掐死教程

高维空间我们感知不到，只能通过投射到三维，甚至二维，直观感受其投影。数学是我们最有力的分析工具。事情直接处理很难，升维或者变维后却变的很简单，处理完后再变换回去，搞定。

三维到二维的投影。欧拉公式所描绘的，是一个随着时间变化，在复平面上做圆周运动的点，随着时间的改变，在时间轴上就成了一条螺旋线。如果只看它的实数部分，也就是螺旋线在左侧的投影，就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。

傅里叶变换（Fourier Transformation）

傅里叶级数和傅里叶变换是什么关系？

马同学原版 · 从傅里叶级数到傅里叶变换

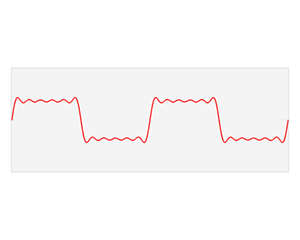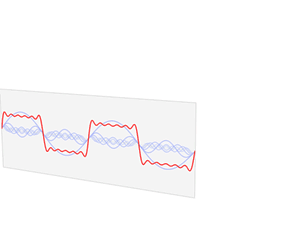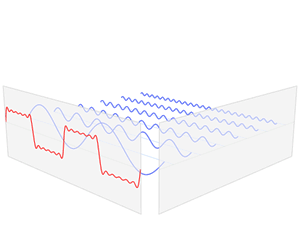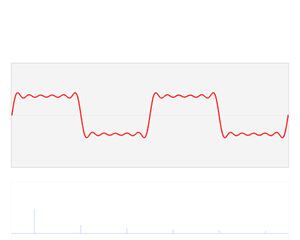
周期函数，可以通过傅里叶级数画出频域图；增长周期，频域图变得越来越密集；当周期无限大，得到傅里叶变换，频域图变为连续的曲线。

傅里叶级数的本质是将一个周期的信号分解成无限多分开的（离散的）正弦波。

傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。是将一个时域非周期的连续信号，转换为一个在频域非周期的连续信号。

形象展示傅里叶变换

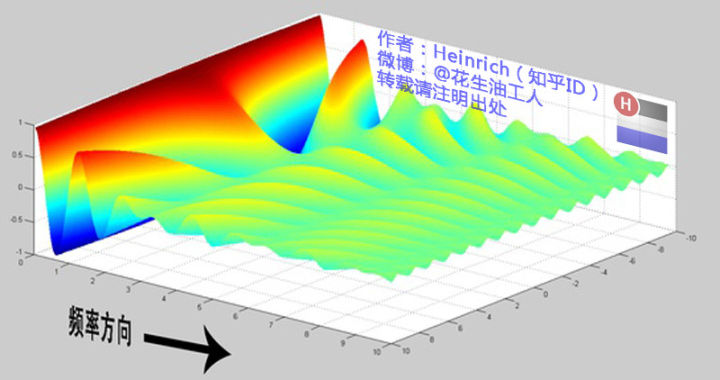
这个视频形象傅里叶级数与傅里叶变换

傅里叶变换是将函数分解到频率不同、幅值恒为 1 的单位圆上；拉普拉斯变换是将函数分解到频率幅值都在变化的圆上。因为拉普拉斯变换的基有两个变量，因此更灵活，适用范围更广。

拉普拉斯变换可视化

3D 动画详细解释傅里叶与拉普拉斯变换

最后这个“海螺图”还是有点没看懂。?

图像傅里叶变换

一个频率相当于一个维度，当维度变成无穷多维度，然后频率叠加就是密度。？

以初中数学基础理解傅里叶变换

形象理解二维傅里叶变换

中心低频贡献了图像的主体，周围高频提供图像的细节和边缘。

为什么用图像二维傅里叶变换的相位谱进行反变换，能够大致得到原图的形状，而幅度谱则不行呢？

k 空间中的 phase 保留的是位置信息，如果没有幅度或者，幅度错误，只是对比度会不同；而 mag 保留的是强度信息，没有 phase 的话，强度相加也是按照周期性相加。

因此：k 空间中的幅度决定强度信息，相位决定位置位置信息。

傅里叶变换、拉普拉斯变换、Z 变换

傅里叶变换、拉普拉斯变换、Z 变换的联系是什么？为什么要进行这些变换？

傅里叶变换是把信号从【时域】变换到【频域】。
拉普拉斯变换是想办法把不满足傅里叶变换条件的【连续信号】从时域变换到频域。
Z 变换是想办法把不满足傅里叶变换条件的【离散信号】从时域变换到频域。

应用举例

PDF 2D Fourier transforms and applications
from http://www.robots.ox.ac.uk/~az/lectures/ia/lect2.pdf

PDF Fourier transform of images
from http://mstrzel.eletel.p.lodz.pl/mstrzel/pattern_rec/fft_ang.pdf 其他课程

螺旋 CT 成像

连原子都能看清的 CT 成像

指纹去噪

天体表面去噪

代码实验

#encoding=utf8
import numpy as np
import matplotlib.pyplot as plt
from scipy import fftpack
from scipy import ndimage
import cv2

def showgray(im, title):
    plt.figure("fft_"+title)
    plt.imshow(im, plt.cm.gray)
    plt.title(title)
    plt.show()

# Show the results
def plotSpectrum(imfft, title):
    plt.figure("fft_"+title)
    from matplotlib.colors import LogNorm
    # A logarithmic colormap
    #plt.imshow(np.abs(imfft), norm=LogNorm(vmin=5))
    magnitudeSpectrum = 20*np.log(np.abs(imfft))
    plt.imshow(magnitudeSpectrum)
    plt.colorbar()
    plt.title(title)
    plt.show()

def plotSpectrum2(srcimg, fshift, title):
    plt.figure("fft_"+title)
    magnitudeSpectrum = 20*np.log(np.abs(fshift))
    plt.subplot(121), plt.imshow(srcimg, cmap = 'gray')
    plt.title('Input Image'), plt.xticks([]), plt.yticks([])
    plt.subplot(122), plt.imshow(magnitudeSpectrum, cmap = 'gray')
    plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
    plt.show()

if __name__ == "__main__":
    im = plt.imread('../image/moonlanding.png').astype(float)
    im = cv2.imread('../image/moonlanding.png', 0).astype(float)
    #showgray(im, 'Original image')

    imfft = fftpack.fft2(im)
    #plotSpectrum(imfft, 'Fourier transform')
    plotSpectrum2(im, imfft, "Original image")

    keepFraction = 0.1
    imfft2 = imfft.copy()
    r, c = imfft2.shape
    imfft2[int(r*keepFraction):int(r*(1-keepFraction)), ...] = 0
    imfft2[..., int(c*keepFraction):int(c*(1-keepFraction))] = 0
    #plotSpectrum(imfft2, 'Filtered Spectrum')

    imnew = fftpack.ifft2(imfft2).real
    #showgray(imnew, 'Reconstructed Image')
    plotSpectrum2(imnew, imfft2, "Reconstructed Image")

    imblur = ndimage.gaussian_filter(im, 4)
    showgray(imblur, 'Blurred image')