图像处理笔记 1/2 -- 灰色图像基础知识 (DIP)

Posted on September 19, 2020 (珠海)
图像处理

第一章 $\Rightarrow$ 第十章

位图基础 & 图像显示

数字图像处理 - Digital Image Processing (DIP)

图像和图形区别

图形是指令的集合，比如 Point1.LineTo(Point2) 。
图像是一个数值矩阵。

索引图像 vs 真色彩图像

索引图像，有颜色表调色板索引。矩阵存储的是索引号。
真色彩图像，矩阵直接存储色彩像素信息。

UltraEdit 软件。基本的编辑文本、十六进制、ASCII 码、语法加亮、代码折叠、代码单词拼写检查等。

图像几何变换

齐次坐标

齐次坐标就是将一个原本是 $n$ 维的向量用一个 $n+1$ 维向量来表示，是指一个用于投影几何里的坐标系统。 这里采用行优先的内存结构，glm::mat4（OpenGL）是列优先记法。

https://zhuanlan.zhihu.com/p/80852438

平移 $\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ 1 \end{array}\right] = \left[\begin{array}{lll} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{l} x \\ y \\ 1 \end{array}\right] = \left[\begin{array}{c} x+\Delta x \\ y+\Delta y \\ 1 \end{array}\right]$

平移 $Translation=\left[\begin{array}{cccc} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{array}\right]$

缩放 $Scale=\left[\begin{array}{cccc} S_{x} & 0 & 0 \\ 0 & S_{y} & 0 \\ 0 & 0 & 1 \end{array}\right]$

旋转 $Rotation=\left[\begin{array}{cccc} \cos \gamma & \sin \gamma & 0 \\ -\sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{array}\right]$

水平镜像 $MirrorReflectionH = \left[\begin{array}{ccc} -1 & 0 & f \text {Width} \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]$

垂直镜像 $MirrorReflectionV = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & -1 & f \text {Height} \\ 0 & 0 & 1 \end{array}\right]$

转置 $Transpose = \left[\begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right]$

错切亦称为剪切或错位变换，包含水平错切和垂直错切，常用于产生弹性物体的变形处理。

错切 $Shear=\left[\begin{array}{cccc} 1 & d_x & 0 \\ d_y & 0 & 0 \\ 0 & 0 & 1 \end{array}\right]$

PPT: https://wenku.baidu.com/view/1bdcc12227c52cc58bd63186bceb19e8b8f6ecbc.html

资料：空间变换网络（STN）原理 + 2D 图像空间变换 + 齐次坐标系讲解。 ^疑似转载 ^貌似原版

仿射变换 & 透视变换

仿射变换（Affine Transformation 或 Affine Map）

是一种二维坐标（x, y）到二维坐标（u, v）的线性变换。仿射变换通过一系列原子变换复合实现，具体包括：平移（Translation）、缩放（Scale）、旋转（Rotation）、翻转（Flip）和错切（Shear）。 https://blog.csdn.net/liuweiyuxiang/article/details/82799999

\[\left\{\begin{array}{l}u=a_{1} x+b_{1} y+c_{1} \\v=a_{2} x+b_{2} y+c_{2}\end{array}\right.\] \[\left[\begin{array}{l}u \\v \\1\end{array}\right]=\left[\begin{array}{lll}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\0 & 0 & 1\end{array}\right]\left[\begin{array}{l}x \\y \\1\end{array}\right]\]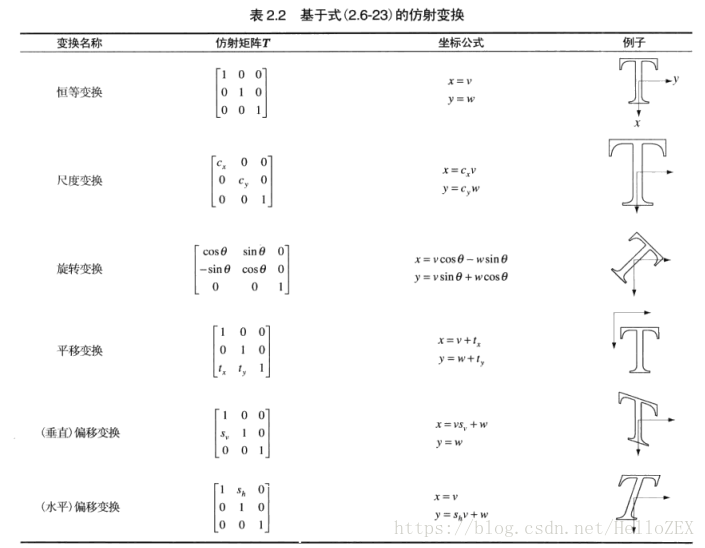

from https://www.cnblogs.com/ghj1976/p/5199086.html

透视变换（Perspective Transformation 或 Viewing Plane / Projective Mapping）

三维

\[\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ 1 \end{array}\right] = \left[\begin{array}{llll} 1 & 0 & 0 & \Delta x \\ 0 & 1 & 0 & \Delta y \\ 0 & 0 & 1 & \Delta z \\ 0 & 0 & 0 & 1 \end{array}\right] \left[\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right] = \left[\begin{array}{c} x+\Delta x \\ y+\Delta y \\ z+\Delta z \\ 1 \end{array}\right]\]

图像灰度变换

点运算：$g(x, y) = T[f(x, y)]$

图像平滑处理

领域处理方法，空域卷积滤波。

中值滤波法。中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。

图像边缘锐化

微分运算，梯度锐化，边缘检测。

\[\nabla f(x, y)=\left[G_{x}, G_{y}\right]^{T}=\left[\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right]^{T}\]

这个矢量的幅度为：

\[\operatorname{mag}(\nabla f)=g(x, y)=\sqrt{\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}}\]

方向角为：

\[\phi(x, y)=\arctan \left|\frac{\partial f}{\partial y} / \frac{\partial f}{\partial x}\right|\]

数字图像中，更多的使用差分来近似导数，最简单的梯度近似表达式如下：

\[\begin{array}{l} G_{x}=f(x, y)-f(x-1, y) \\ G_{y}=f(x, y)-f(x, y-1) \end{array}\]

拉普拉斯算子

二阶微分，拉普拉斯算子。

\[\begin{array}{l} \nabla^2 f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}} \\ \frac{\partial^{2} f}{\partial x^{2}}=f(x+1)+f(x-1)-2 f(x) \\ \frac{\partial^{2} f}{\partial y^{2}}=f(y+1)+f(y-1)-2 f(y) \\ \end{array}\]

两个分向量相加：

\[\nabla^2 f=[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]-4f(x,y)\]

原始图像和拉普拉斯图像叠加，可以边缘加强。

\[g(x)= \begin{cases} f(x, y)-\nabla^{2} f(x, y) & \text{ 中心系数为负 } \\ f(x, y)+\nabla^{2} f(x, y) & \text{ 中心系数为正 } \end{cases}\]

边缘检测，LOG 算子（高斯-拉普拉斯算子 / Laplacian of Gaussian, LoG）中心点的距离与位置加权系数的关系：

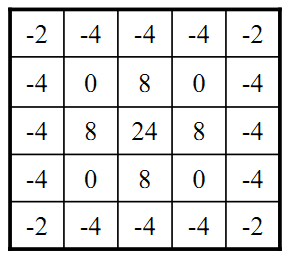
推演过程。高斯二阶导如下图的绿色线，蓝色线是高斯一阶导数，红色则是高斯函数。

高频提升滤波器

\[g(x,y)=af(x,y)\pm \nabla f(x,y)\]

边缘检测

\[\begin{array}{|c|c|c|} \hline Z_{1} & Z_{2} & Z_{3} \\ \hline Z_{4} & Z_{5} & Z_{6} \\ \hline Z_{7} & Z_{8} & Z_{9} \\ \hline \end{array}\]

Roberts 边缘检测算子

Robert 交叉微分算子。

\[\nabla f \approx\left|z_{9}-z_{5}\right|+\left|z_{8}-z_{6}\right|\]

Sobel 边缘检测算子

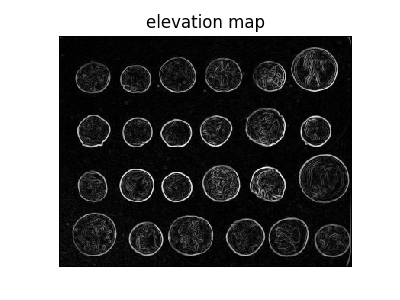
\[\begin{array}{l} G_{x}=\left(Z_{7}+2 Z_{8}+Z_{9}\right)-\left(Z_{1}+2 Z_{2}+Z_{3}\right) \\ G_{y}=\left(Z_{3}+2 Z_{6}+Z_{9}\right)-\left(Z_{1}+2 Z_{4}+Z_{7}\right) \end{array}\]

浮雕特效。从下面显示的三维表面图中，我们看到高屏障有效地将硬币从背景中分离出来。from

Prewitt 边缘检测算子

\[\begin{array}{l} G_{x}=\left(Z_{7}+Z_{8}+Z_{9}\right)-\left(Z_{1}+Z_{2}+Z_{3}\right) \\ G_{y}=\left(Z_{3}+Z_{6}+Z_{9}\right)-\left(Z_{1}+Z_{4}+Z_{7}\right) \end{array}\]

Krisch 边缘检测算子

图像中的每个点都用 8 个掩模进行卷积，取八个方向的最大值作为边缘幅值的输出。掩模序号对应边缘方向的编码。卷积的结果进行比较时，比较这个八个数的绝对值，因为，这个代表的是梯度，正负号只是方向。

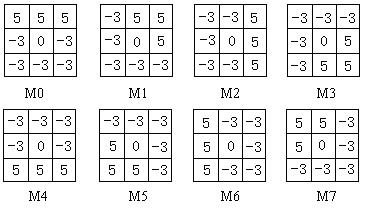
LoG_Laplacian 高斯-拉普拉斯算子

\[\left[\begin{array}{ccccc} -2 & -4 & -4 & -4 & -2 \\ -4 & 0 & 8 & 0 & -4 \\ -4 & 8 & 24 * & 8 & -4 \\ -4 & 0 & 8 & 0 & -4 \\ -2 & -4 & -4 & -4 & -2 \end{array}\right]\]

图像分割及测量

graph LR A[图像] --> B[图像预处理] B --> | 图像分割 |C[图像识别] C --> D[图像理解] classDef orange fill:#f96; class E orange;

迭代法求取阈值进行图像分割

图像分割后的两部分 A 和 B 的均值和基本保持稳定。也就是说，随着迭代的进行，取 $[mean(A)+mean(B)]/2$ 最终的收敛值作为分割阈值。

轮廓提取

轮廓提取法

对于二值图像的轮廓提取，我们可以采用掏空内部点法，如果原图中有一点为黑，且它的 8 个相邻的点都为黑，则将该点删除。对于非二值图像，要先进行二值处理。

边界跟踪法

从图像的某个边界点出发，然后按照某种策略，搜索下一个边界点。直到搜索点与初始点重合，即找到轮廓。

区域增长法

依次用图像的每一个像素的灰度值和种子点相减，判断结果是否小于标准差，如果小于则将该点和种子点合并，不是则保持像素点的灰度值不变。这样处理后的图像就用区域分割法处理后的边缘分割图像

三个要点：

选择合适的种子点
确定相似性条件
确定停止生长的条件

区域分裂合并法

利用金字塔或者四叉树数据结构的层次概念，将图像划分成一组任意不相交的初始区域，即从金字塔或者四叉树结构的任意中间层开始，根据给定的均匀性检测准则进行分裂和合并这些区域。逐步改善区域划分性能，直到最后将图像分成数量最少的均匀区域为之。

如何确定区域的相似性呢？基于区域的灰度值，或者基于区域边界的强弱项。简单的方法就下比较他们的灰度均值。

图形分割

图像的面积与周长计算，二值化图像区域标记。https://www.cnblogs.com/-wenli/p/11722469.html

灰度转换算法 https://www.cnblogs.com/-wenli/p/11562327.html

图像的测量之投影与纹理

https://blog.csdn.net/qq_43409114/article/details/104714828

课件

衡量直方图间的相似性

直方图的均值，直方图的方差。直方图统计了相同像素的个数。

直方图的均值：（该区域每一个像素 * 该像素的个数）/ 该区域像素点个数
直方图的方差：（该区域每一个像素 - 均值）^ 2 * 该像素的个数）/ 该区域像素点个数

设 $h_1(z)$ 和 $h_2(z)$ 为两个区域的灰度直方图。

\[m_{1}=\frac{\sum z h_{1}(z)}{\sum h_{1}(z)} \quad \sigma_{1}^{2}=\frac{\sum\left(z-m_{1}\right)^{2} h_{1}(z)}{\sum h_{1}(z)}\] \[m_{2}=\frac{\sum z h_{2}(z)}{\sum h_{2}(z)} \quad \sigma_{2}^{2}=\frac{\sum\left(z-m_{2}\right)^{2} h_{2}(z)}{\sum h_{2}(z)}\]

other

其他资料对于两直方图 $S=\left\{ {s_{1}},\cdots {s_{n}} \right\}$ 及 $M=\left\{ {m_{1}},\cdots {m_{n}} \right\}$，$n$ 为直方图维数（如 255），这两直方图之间的卡方相似性为：

\[\chi_ \omega ^{2}(S,M)= \sum\limits_{i=1}^{n}{ { \omega _{i}}\frac{ { {\left( {s_{i}}-{m_{i}} \right)}^{2}}}{ { s_{i}}+{m_{i}}}}\]

其中，${\omega _{i}}$ 为权重，可令不同维度权重取不同值。

直方图欧氏距离的相似性度量 为：

\[D(S,M)={ { \left( \sum\limits_{i=1}^{n}{ { {\left( {s_{i}}-{m_{i}} \right)}^{2}}} \right)}^{2}}\]

其中，$0 \le {s_{i}}\le 1$ 和 $0 \le {m_{i}}\le 1$ 为归一化值（此处外部是平方还是 0.5 次方不确定）。

归一化处理后，图像直方图的相似度的度量为：

\[D(S,M)=\frac{1}{n}\sum\limits_{i=1}^{n}{\left( 1-\frac{\left| { { s}_{i}}-{m_{i}} \right|}{\max ({ { s}_{i}},{m_{i}})} \right)}\]

直方图相似性常用于人脸检测。

Kolmogorov-Smirnov 检测法

对于两幅图像，分别求出其累计直方图，然后取其累计直方图差值的最大值。

\[\begin{array}{c} H(z)=\int_{0}^{z} h(x) d x \\ K S=\max_z \left|H_{1}(z)-H_{2}(z)\right| \end{array}\]

然后再求出直方图之间差值的的和值，为 $SD$：

\[S D=\sum_z \left|h_{1}(z)-h_{2}(z)\right|\]

如果 $\vert KS−SD\vert$ 在阈值之内，则相似。

def Texture_2(img1, img2):
    # 下面是用来求一副图像的直方图
    def getStatic(img):
        static = np.zeros(shape=256, dtype=int)
        for y in range(0, len(img)):
            for x in range(0, len(img[y])):
                c = img[y, x, 0]
                static[c] = static[c] + 1
        return static

    # 下面的函数是用来求一副图像的累计直方图
    def getStatic1(img):
        static = np.zeros(shape=256, dtype=int)
        for y in range(0, len(img)):
            for x in range(0, len(img[y])):
                c = img[y, x, 0]
                static[c] = static[c] + 1
                if c > 0:
                    static[c] = static[c] + static[c-1]
        return static
    static1 = getStatic(img1)
    static2 = getStatic(img2)
    # 用来参数 KS
    KS = np.max(static1 - static2)
    # 用来求参数 SD
    SD = np.sum((getStatic(img1) - getStatic(img2)), axis=0)
    return np.abs(KS - SD)

图像自相关函数分析法

\[p(x, y)=\frac{\sum_{i=0}^{N-1} \sum_{j=0}^{N-1} f(i, j) f(i+x, j+y)}{\sum_{i=0}^{N-1} \sum_{j=0}^{N-1} f(i, j)}\] \[d=\left(x^{2}+y^{2}\right)^{\frac{1}{2}}\]

灰度共生矩阵特征分析法

为从灰度为 $i$ 的像素点出发，离开某个固定位置 $\sigma=(dx,dy)$ 的另一个像素点的同时发生的灰度为 $j$，定义这两个灰度在整个图像中发生的概率（或者频率）。

还没看懂。

灰度-梯度共生矩阵分析法

图像形态学

形态学的基本操作包括腐蚀、膨胀、开操作、闭操作。

简单来说，以 B 结构中心点为准心，在 A 中找能满足 B 结构的点即为腐蚀。把 A 结构的每个点放到 B 中心点，以 B 结构外扩即为膨胀。开操作表示先腐蚀后膨胀；闭操作表示先膨胀后腐蚀。

闭运算，弥合，毛刺保留；开运算，分裂，毛刺去掉。from

开运算（open） ：先腐蚀后膨胀的过程。开运算可以用来消除小黑点，在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积。
闭运算（close） ：先膨胀后腐蚀的过程。闭运算可以用来排除小黑洞。
形态学梯度（morph-grad） ：可以突出团块（blob）的边缘，保留物体的边缘轮廓。
顶帽（top-hat） ：将突出比原轮廓亮的部分。
黑帽（black-hat） ：将突出比原轮廓暗的部分。

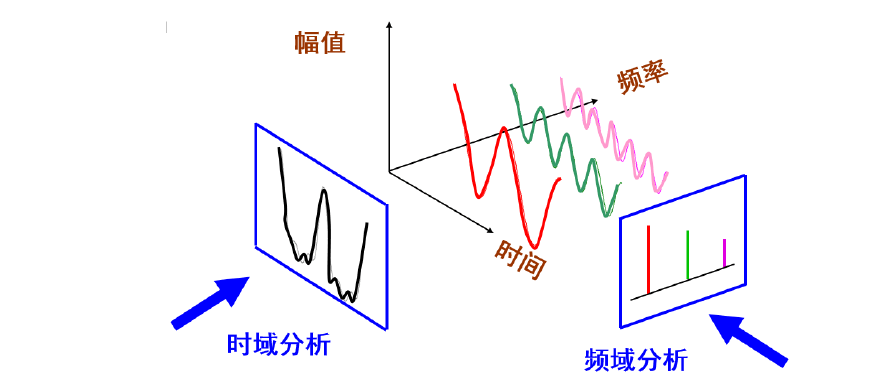
图像变换域处理

纯干货傅里叶变换

空域 vs 频域 vs 时域。

傅里叶变换

一脸懵逼，没看懂。单独开了一篇文章。傅里叶变换 /blog/2020/09/26/dip-fourier-transform

一维傅里叶变换及逆变换 https://blog.csdn.net/Ciellee/article/details/108359201

一维傅里叶变换：

\[F(u) = \sum_{M=0}^{M-1} f(x) e^{-j u x \frac{2\pi} M}， u=0,1,2,\cdots,M-1\]

一维傅里叶逆变换：

\[f(x) = {\frac 1 M} \sum_{u=0}^{M-1} F(u) e^{j u x \frac{2\pi} M}， x=0,1,2,\cdots,M-1\]

代入欧拉公式：

\[e^{jx} = \cos(x) + j \sin(x)\] \[e^{-jx} = \cos(x) - j \sin(x)\] \[e^{j\pi} + 1 = 0\] \[\sin(x) = \frac {e^{ix} - e^{-jx}} {2i}\] \[\cos(x) = \frac {e^{ix} + e^{-jx}} {2i}\]

我们可以得到如下：

一维傅里叶变换：

\[F(u) = \sum_{M=0}^{M-1} f(x) \left( e^{-j u x \frac{2\pi} M} \right)， u=0,1,2,\cdots,M-1 \\ \Rightarrow F(u) = \sum_{M=0}^{M-1} f(x) \left( \cos(u x \frac{2\pi} M) - j \sin(u x \frac{2\pi} M) \right)， u=0,1,2,\cdots,M-1\]

一维傅里叶逆变换：

\[f(x) = {\frac 1 M} \sum_{u=0}^{M-1} F(u) e^{j u x \frac{2\pi} M}， x=0,1,2,\cdots,M-1 \\ \Rightarrow f(x) = {\frac 1 M} \sum_{u=0}^{M-1} F(u) \left( \cos(u x \frac{2\pi} M) + j \sin(u x \frac{2\pi} M) \right) ， x=0,1,2,\cdots,M-1\]

在计算每个 $F(u)$ 时，由于一维傅里叶逆变换中的 $u$ 是一个复数，假设复数 $F(u) = a + b j$ ，将 $u$ 代入逆变换中，得到如下：

\[f(x) = {\frac 1 M} \sum_{u=0}^{M-1} F(u) \left( \cos(u x \frac{2\pi} M) + j \sin(u x \frac{2\pi} M) \right) ， x=0,1,2,\cdots,M-1\]

对于每个 $F(u)$ ，实部虚部计算结果如下：

\[f(x) = ( a + b j) \left( \cos(u x \frac{2\pi} M) + j \sin(u x \frac{2\pi} M) \right)\] \[f(x) =\left( a\cos(u x \frac{2\pi} M) + bj\cos(u x \frac{2\pi} M) + aj \sin(u x \frac{2\pi} M) + bj\cdot j \sin(u x \frac{2\pi} M) \right)\]

分离虚部，实部结果如下：

\[f(x).real =\left( a\cos(u x \frac{2\pi} M) - b \sin(u x \frac{2\pi} M) \right)\] \[f(x).imag =\left( a \sin(u x \frac{2\pi} M) + b\cos(u x \frac{2\pi} M) \right) \cdot j\]

这里有几张图。BMP 图像的 FFT 快速傅里叶变换及 IFFT 逆变换

源代码：https://blog.csdn.net/cp1300/article/details/28850309

#ifndef __FFT_H__
#define __FFT_H__

typedef struct complex // 复数类型
{
   float real; // 实部
   float imag; // 虚部
} complex;

#define PI 3.1415926535897932384626433832795028841971

// 使用 fft(FFT_NPT, fft_buff); // 进行 FFT 处理
void conjugate_complex(int n, complex in[], complex out[]);
void c_plus(complex a, complex b, complex *c); // 复数加
void c_mul(complex a, complex b, complex *c) ; // 复数乘
void c_sub(complex a, complex b, complex *c); // 复数减法
void c_div(complex a, complex b, complex *c); // 复数除法
void fft(int N, complex f[]); // 傅立叶变换 输出也存在数组 f 中
void ifft(int N, complex f[]); // 傅里叶逆变换
void c_abs(complex f[], float out[], int n); // 复数数组取模

#endif

离散余弦变换

一脸懵逼，没看懂。

图像的离散余弦变换广泛用于图像的压缩。对原始图像进行离散余弦变换，变换后 DCT 系数能量主要集中在左上角，其余大部分系数接近于零，DCT 具有适用于图像压缩的特性。将变换后的 DCT 系数进行门限操作，将小于一定值得系数归零，这就是图像压缩中的量化过程，然后进行逆 DCT 运算，可以得到压缩后的图像。

离散余弦变换（含源码）

参考

参考资料快照

本文短链接：
If you have any questions or feedback, please reach out