机器学习 -- 卡尔曼滤波(Kalman filtering)
草履虫都能看懂的 卡尔曼滤波 。
卡尔曼滤波(Kalman filtering)一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。 由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
原理
卡尔曼滤波器是一种基础预测定位算法。原理非常简单易懂。核心过程可以用一个图说明:
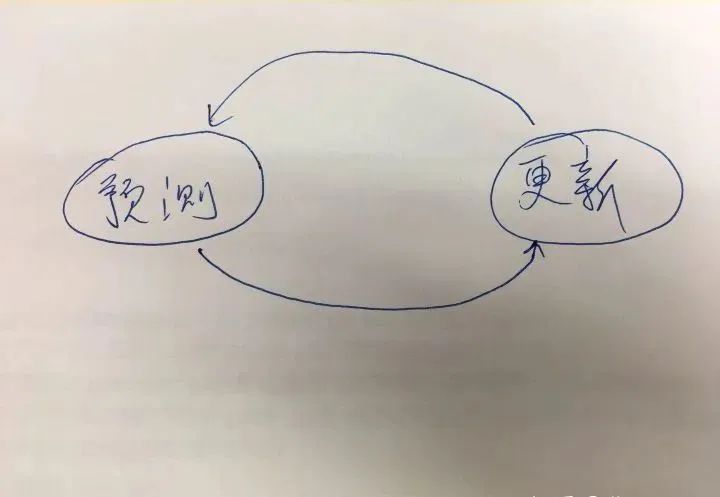
本质上就是这两个状态过程的迭代,来逐步的准确定位。
预测:当前状态环境下,对下一个时间段 t 的位置估计计算的值。
更新:更具传感器获取到比较准确的位置信息后来更新当前的预测问位置,也就是纠正预测的错误。
你可能要问为什么有传感器的数据了还要进行更新?因为在现实世界中传感器是存在很多噪声干扰的,所以也不能完全相信传感器数据。卡尔曼算法依赖于线性计算,高斯分布,我们以一维定位来介绍算法的实现。
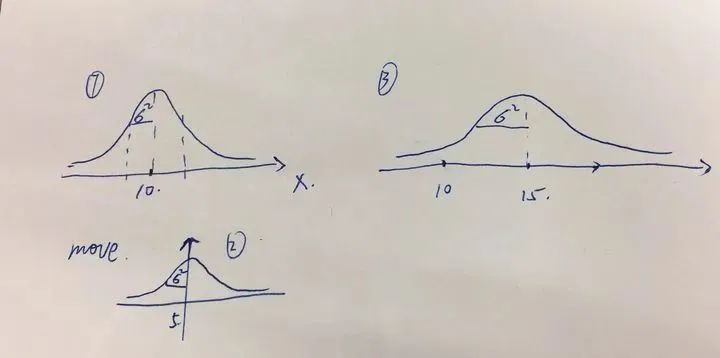

接下来我们开更新,预测后我们获取到传感器数据,表示目前传感器发现小车的位置应该是在 26 这个位置,在这种情况下,我们肯定是觉得传感器的准确度比我之前的预测瞎猜要来的准确。
所以方差自然会比较小,最终我们觉得真是的小车位置应该是更靠近传感器数据的,而且方差会缩小,以至于,想想也很清楚,我猜了一个预测值,现在有个专家告诉了我相对比较靠谱的数据,那我对小车的位置的自信度肯定会上升啊。
最终小车的位置经过这个时间段 t 的更新就是下图红色的高斯图:
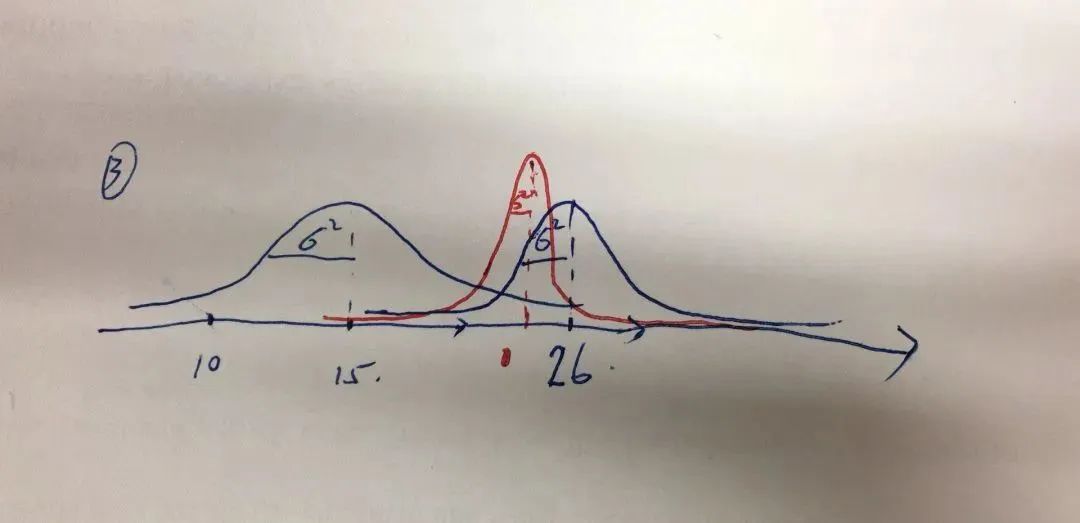
一维模型下的 Kalman 公式:
预测
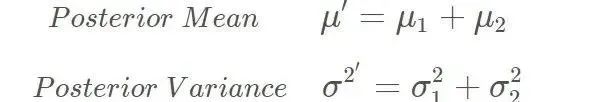
更新
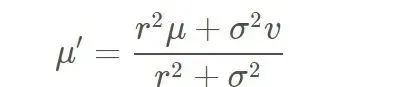
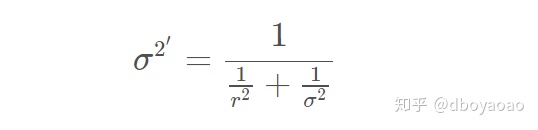
参考代码
#include <iostream>
#include <math.h>
#include <tuple>
using namespace std;
double new_mean, new_var;
tuple<double, double> measurement_update(double mean1, double var1, double mean2, double var2)
{
new_mean = (var2 * mean1 + var1 * mean2) / (var1 + var2);
new_var = 1 / (1 / var1 + 1 / var2);
return make_tuple(new_mean, new_var);
}
tuple<double, double> state_prediction(double mean1, double var1, double mean2, double var2)
{
new_mean = mean1 + mean2;
new_var = var1 + var2;
return make_tuple(new_mean, new_var);
}
int main()
{
//Measurements and measurement variance
double measurements[5] = { 5, 6, 7, 9, 10 };
double measurement_sig = 4;
//Motions and motion variance
double motion[5] = { 1, 1, 2, 1, 1 };
double motion_sig = 2;
//Initial state
double mu = 0;
double sig = 1000;
for (int i = 0; i < sizeof(measurements) / sizeof(measurements[0]); i++) {
tie(mu, sig) = measurement_update(mu, sig, measurements[i], measurement_sig);
printf("update: [%f, %f]\n", mu, sig);
tie(mu, sig) = state_prediction(mu, sig, motion[i], motion_sig);
printf("predict: [%f, %f]\n", mu, sig);
}
return 0;
}
refs
参考资料快照
草履虫 系列文章
- 机器学习 -- 正态分布中为什么有 π? | 13 Aug 2023
- 机器学习 -- 卡尔曼滤波(Kalman filtering) | 17 Jun 2023
- 机器学习 -- 极大似然估计(MLE,Maximum Likelihood Estimation) | 13 Jun 2023
参考资料快照
 .
.