MATHEMATICS -- 黎曼猜想
数学界的三大高峰:欧拉、高斯和黎曼。其中,欧拉的数学技巧无与伦比;高斯的数学才能绝无仅有;而黎曼的数学灵感,足够让其他数学家忙碌几百年。 简单的列一下:
$\zeta$ 函数 \(\zeta(s)=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\cdots\\\)
当定义域在实数的时候,欧拉证明:
- 当 $s=1$ 时,就变成了著名的调和级数,是不收敛的。
- 当 $s<1$ 时,加的项会逐渐变大,最后的结果会趋于正无穷,也是不收敛的。
- 当 $s>1$ 时,加的项越来越小,可以想象它最后会趋于一个实数,我们称这种趋于一个数的情况为收敛的。
黎曼把这个函数进行了 解析延拓 ,定义域扩展到了复平面。 \(\zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^{s}}(\operatorname{Re}(s)>1)\) 只要 $s$ 的实部大于 1,就是收敛的。
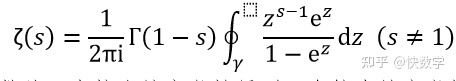
令这个函数等于 0,求解: Obviously,当 $s$ 为负偶数时,$ζ(s)$ 为 0,这些零点被称为平凡零点, $ζ(s)$ 的其他零点被成为非平凡零点。
黎曼猜想(Riemann Hypothesis):黎曼 $\zeta$ 函数的非平凡零点实部均为 1/2。

https://www.zhihu.com/question/295496241/answer/1894897469
数学中的皇冠 —— 数论 —— 2000 年来一直没有任何实际应用,是最纯粹的数学。直到计算机,尤其是现代密码学的出现,才让数论第一次走出数学,走进了人们的生活中。
如果真的有神的话,那么数学就是神的语言。 心事浩茫连广宇,于无声处听惊雷。
大概讲的是,一个牛逼的函数,对于任意输入数字 $x$,可以直接算出小于 $x$ 的所有质数个数。
黎曼素数计数函数:
\[J(x)=Li(x)-\sum_{\rho}Li(x^{\rho})-\ln 2 +\int_x^\infty\frac{dt}{t(t^2-1)\ln t}\]当代入的非平凡零点越多,越准确。
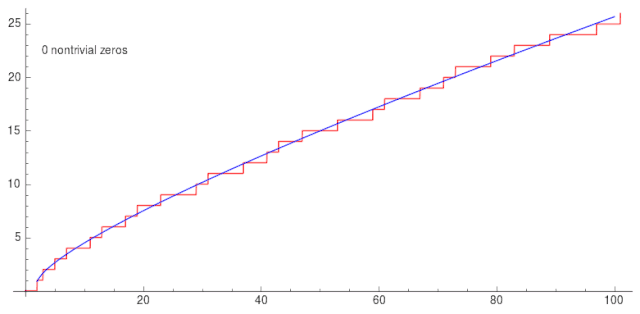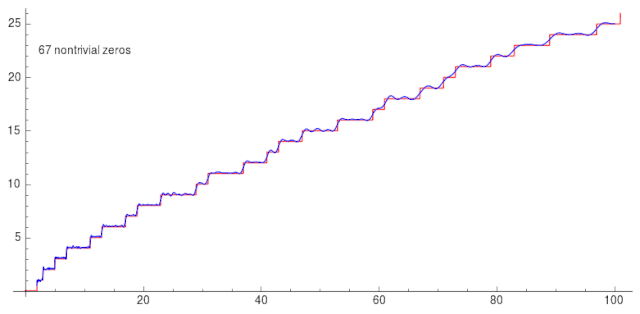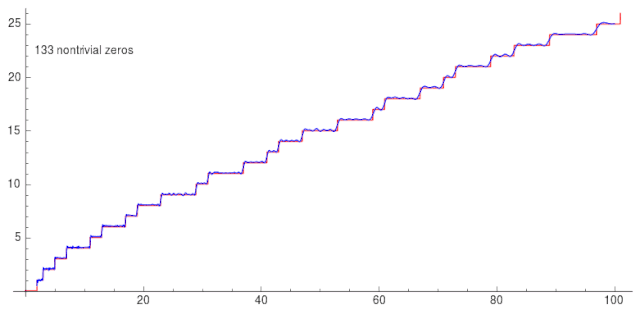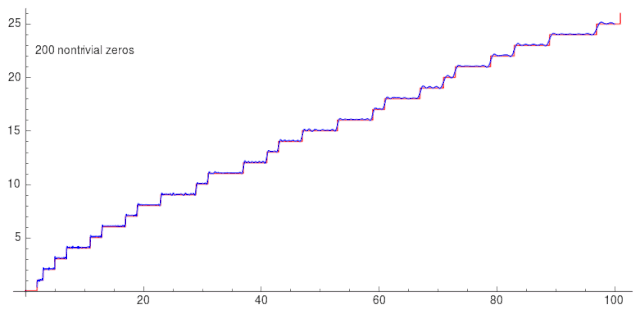
而黎曼猜想说的是,这些非平凡零点的所有实部都是 1/2。
严伯钧说:能完全理解黎曼猜想,至少是一个数学专业的博士生水平。一切的起点:欧拉乘积公式,对于全体质数的某种运算,可以转移成对于全体自然数的某种运算。
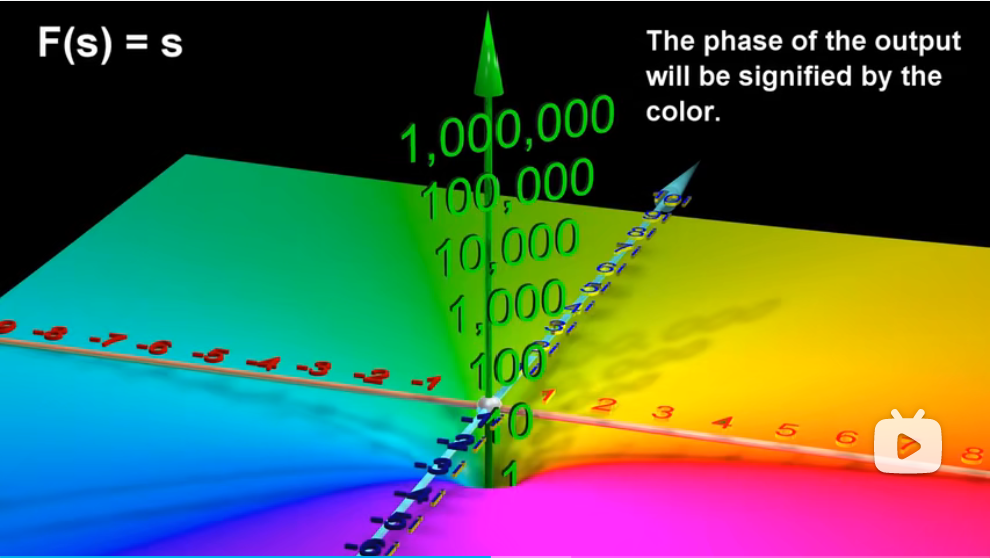
复数到复数的函数,四维空间才可以表示出来。 magnitude(幅度)表示大小,phase(相位)用颜色表示。
马同学
黎曼猜想(Riemann hypothesis)是什么?有什么用?
李永乐老师
-
欧拉级数 解析延拓
解析延拓
- 需要处处可导
- 给数学系用的复变函数教程上都会讲到,只要在一个有聚点的点集上给定了函数值,那么无论怎样做解析延拓,都只能有唯一的结果。
- 任何两个全纯函数,如果在一个区域内相等,则它们在任何一点处都相等。因此,解析延拓是唯一的。
科技袁人
-
黎曼猜想合集-总有一天,人类会骄傲地发出这串数字:2,3,5,7,11……
质数的分布函数
-
黎曼猜想合集-总有一天,人类会骄傲地发出这串数字:2,3,5,7,11……
论小于给定数值的质数个数
质数定理
袁岚峰
- 理解黎曼猜想(一)背景 | 袁岚峰
- 理解黎曼猜想(二)两个自然数互质的概率是多少? | 袁岚峰
- 理解黎曼猜想(三)你真的相信全体自然数的和等于 -1/12 吗? | 袁岚峰
- 理解黎曼猜想(四)得救之道,就在其中 | 袁岚峰
- 理解黎曼猜想(五)宇宙的密码 | 袁岚峰
- 理解黎曼猜想(六)朝闻道 | 袁岚峰
3Blue1Brown
CSDN 其它文章
实际应用
和密码学关系重大。
参考资料快照
- https://www.zhihu.com/question/295496241/answer/1894897469
- https://zhuanlan.zhihu.com/p/25055731
- https://zhuanlan.zhihu.com/p/25222934
- https://www.matongxue.com/madocs/2101
- https://www.zhihu.com/question/295619713
- https://www.bilibili.com/video/BV1MW411S7Tg
- https://www.bilibili.com/video/BV1HW411S77f
- https://www.bilibili.com/video/BV1rW411m7GL
- https://www.bilibili.com/video/BV1vt411b72q
- https://www.bilibili.com/video/BV1vt411b72q?p=2
- https://zhuanlan.zhihu.com/p/47346148
- https://zhuanlan.zhihu.com/p/47978393
- https://zhuanlan.zhihu.com/p/48750070
- https://zhuanlan.zhihu.com/p/49454034
- https://zhuanlan.zhihu.com/p/50421799
- https://zhuanlan.zhihu.com/p/51566599
- https://www.bilibili.com/video/BV1tx411y7VG
- https://blog.csdn.net/fztsilly/article/details/106525876
- https://blog.csdn.net/fztsilly/article/details/106549849
- https://blog.csdn.net/fztsilly/article/details/106548223
- https://blog.csdn.net/qq_40155097/article/details/86670230

 .
.