图像处理笔记 -- 数字图像处理 (DIP)
拉普拉斯变换
拉普拉斯变换不是一堆独立公式,而是一套“操作规则”。 常用公式几乎都能从:
- 一个起点函数
- 几个基本操作
反复组合得到 。
起点函数
\[\mathcal L{1}=\frac1s\]这是整张常用表的源头,其它函数都是在它上面“加工”出来的。
第一条主线:时间积分 → 幂函数
时间积分在拉普拉斯域中对应 除以 (s) :
\[\mathcal L\left\{\int_0^t f(\tau)d\tau\right\}=\frac1s F(s)\]从 (1) 出发:
\[1 \xrightarrow{\int} t \xrightarrow{\int} \frac{t^2}{2!} \xrightarrow{\int} \cdots\]对应频域:
\[\frac1s \to \frac1{s^2} \to \frac1{s^3} \to \cdots\]整理得到:
\[\mathcal L{t^n}=\frac{n!}{s^{n+1}}\]结论 :
时间里多一个 (t),频域里多一个 (s) 在分母
第二条主线:指数函数 → 频域平移
由定义直接看指数项:
\[e^{at}e^{-st}=e^{-(s-a)t}\]因此有性质:
\[\mathcal L{e^{at}f(t)}=F(s-a)\]套在起点函数上:
\[1 \to e^{at} \quad\Rightarrow\quad \mathcal L{e^{at}}=\frac1{s-a}\]再套在幂函数上:
\[\mathcal L{t^n e^{at}}=\frac{n!}{(s-a)^{n+1}}\]结论 :
时域乘 (e^{at}),等价于频域中 (s) 整体平移
第三条主线:三角函数来自指数
三角函数不是新东西,而是 复指数的分解 :
\[e^{j\omega t}=\cos\omega t+j\sin\omega t\]先算复指数:
\[\mathcal L{e^{j\omega t}}=\frac1{s-j\omega}\]取实部、虚部:
\[\mathcal L{\cos\omega t}=\frac{s}{s^2+\omega^2}, \quad \mathcal L{\sin\omega t}=\frac{\omega}{s^2+\omega^2}\]结论 :
记住复指数,sin / cos 自动出现
第四条主线:微分 → 频域乘 (s)
由分部积分得到:
\[\mathcal L{f'(t)}=sF(s)-f(0^+)\]再微分一次:
\[\mathcal L{f''(t)}=s^2F(s)-sf(0^+)-f'(0^+)\]结论 :
求导就是乘 (s),但必须扣掉初值
第五条主线:时间平移 → 指数因子
函数从 (t=a) 才开始:
\[f(t-a)u(t-a)\]拉普拉斯变换为:
\[\mathcal L{f(t-a)u(t-a)}=e^{-as}F(s)\]结论 :
时域右移 (a),频域多一个 (e^{-as})
最终“脑内流程图”(可顺着推)
1
↓ 积分
t → tⁿ
↓ 乘 e^{at}
e^{at}, tⁿe^{at}
↓ 复指数分解
sin / cos
↓ 求导
f', f''
↓ 时间平移
f(t-a)
一句话版本(考场用)
从 1 出发:积分出幂,指数移 s,复指数出三角,求导乘 s 减初值,右移乘指数。
只要你记住这句话, 整张常用拉普拉斯表都能顺着推出来 。
离散傅里叶变换 DFT 的计算
DFT 的计算 例:一维函数的四个采样值为 $f(0)=2$, $f(1)=3$, $f(2)=f(3)=4$。
① 分组
\[f(n) \begin{cases} \{f(0), f(2)\} & \text{Even} \\ \{f(1), f(3)\} & \text{Odd} \end{cases}\]② 旋转因子计算
\[W_N = e^{-j\frac{2\pi}{N}}\] \[W_4^0 = e^{0} = 1\] \[W_4^1 = e^{-j\frac{2\pi}{4}} = e^{-j\frac{\pi}{2}} = \cos(-\frac{\pi}{2}) + j\sin(-\frac{\pi}{2}) = -j\]偶数组和奇数组的 2 点 DFT
\[F_{even}^2(0) = \frac{1}{2}[f(0) + f(2)W_2^0] = \frac{1}{2}(2+4) = 3\] \[F_{even}^2(1) = \frac{1}{2}[f(0) - f(2)W_2^0] = \frac{1}{2}(2-4) = -1\] \[F_{odd}^2(0) = \frac{1}{2}[f(1) + f(3)W_2^0] = \frac{1}{2}(3+4) = \frac{7}{2}\] \[F_{odd}^2(1) = \frac{1}{2}[f(1) - f(3)W_2^0] = \frac{1}{2}(3-4) = -\frac{1}{2}\]最终 4 点 DFT 结果
\[F(0) = \frac{1}{2}[F_{even}^2(0) + F_{odd}^2(0)W_4^0] = \frac{1}{2}[3 + \frac{7}{2} \cdot 1] = \frac{13}{4} = 3.25\] \[F(1) = \frac{1}{2}[F_{even}^2(1) + F_{odd}^2(1)W_4^1] = \frac{1}{2}[-1 + (-\frac{1}{2}) \cdot (-j)] = -\frac{1}{2} + \frac{j}{4}\] \[F(2) = \frac{1}{2}[F_{even}^2(0) - F_{odd}^2(0)W_4^0] = \frac{1}{2}[3 - \frac{7}{2}] = -\frac{1}{4}\] \[F(3) = \frac{1}{2}[F_{even}^2(1) - F_{odd}^2(1)W_4^1] = \frac{1}{2}[-1 - (-\frac{1}{2}) \cdot (-j)] = -\frac{1}{2} - \frac{j}{4}\]4 邻域均值低通滤波器的频域表示

利用像素点 $(x, y)$ 的 4 近领域(不包括该点)组成一个低通滤波器。 写出与它等价的频域滤波函数。
原始图像
\[f(x,y)\]滤波后的图像
\[g(x,y)\]用 4 个邻居平均
\[\boxed{ g(x,y) =\frac14\Big[ f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1) \Big] }\]傅里叶“平移公式”。如果 \(f(x,y) \xrightarrow{\mathcal{F}} F(u,v)\)
那么 \(f(x+a,y+b) \xrightarrow{\mathcal{F}} F(u,v)e^{j2\pi(\frac{au}{M}+\frac{bv}{N})}\)
对应到本题的 4 种情况:
| 空间域 | 频域 |
|---|---|
| $f(x+1,y)$ | $F(u,v)e^{j\frac{2\pi u}{M}}$ |
| $f(x-1,y)$ | $F(u,v)e^{-j\frac{2\pi u}{M}}$ |
| $f(x,y+1)$ | $F(u,v)e^{j\frac{2\pi v}{N}}$ |
| $f(x,y-1)$ | $F(u,v)e^{-j\frac{2\pi v}{N}}$ |
我们对 \(g(x,y) =\frac14[\cdots]\) 两边同时做傅里叶变换
左边:
\[g(x,y) \xrightarrow{\mathcal{F}} G(u,v)\]右边(逐项变换):
\[\begin{aligned} G(u,v) &=\frac14\Big[ F(u,v)e^{j\frac{2\pi u}{M}} +F(u,v)e^{-j\frac{2\pi u}{M}} \\ &\quad\quad +F(u,v)e^{j\frac{2\pi v}{N}} +F(u,v)e^{-j\frac{2\pi v}{N}} \Big] \end{aligned}\]把公共因子提出来, 你会发现 每一项都有 $F(u,v)$ :
\[\begin{aligned} G(u,v) &=F(u,v)\cdot \frac14\Big( e^{j\frac{2\pi u}{M}} +e^{-j\frac{2\pi u}{M}} \\ &\quad\quad +e^{j\frac{2\pi v}{N}} +e^{-j\frac{2\pi v}{N}} \Big) \end{aligned}\]这一步的意义是:
\[\boxed{ G(u,v)=F(u,v)\cdot H(u,v) }\]括号里的东西,就是 频域滤波器 $H(u,v)$。
根据公式:
\[\boxed{ e^{j\theta}+e^{-j\theta}=2\cos\theta }\]应用到这里:
\[\begin{aligned} H(u,v) &=\frac14\Big( 2\cos\frac{2\pi u}{M} +2\cos\frac{2\pi v}{N} \Big) \\ &=\boxed{ \frac12\Big( \cos\frac{2\pi u}{M} +\cos\frac{2\pi v}{N} \Big) } \end{aligned}\]最终答案
\[\boxed{ H(u,v)=\frac12\left( \cos\frac{2\pi u}{M} +\cos\frac{2\pi v}{N} \right) }\]并且
\[\boxed{ G(u,v)=F(u,v) H(u,v) }\]色彩模型
面向设备的色彩模型 RGB CMYK
面向色彩感知的色彩模型 HSI LAB
RGB 模型 —— 面向输出显示设备
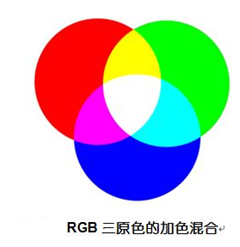
RGB 模型是基于仿生学原理,人的视网膜有三种细胞,分别对红、绿、蓝三种颜色敏感(其中绿色最敏感)。这三种颜色的光通过相加,可以混合出绝大部分肉眼能看到的颜色。 使用最广泛的色彩模型。非常适合在输出显示场合使用,如彩色电视机的显像管、计算机的显示器。
国际照度委员会规定 3 种基本色的波长为 R:700nm,G:546.1nm,B:435.8nm。
CMYK 模型 —— 面向输出印刷设备
CMYK 色彩系统是一种用于印刷的模式,分别是指青(Cyan)、品红(Magenta)、黄(Yellow)和黑(Black)。
CMYK 模式在本质上与 RGB 颜色模式没有什么区别,只是产生色彩的原理不同。RGB 颜色合成是通过颜色相加。而 CMYK 是通过颜色相减产生其它颜色。 RGB 与 CMYK 没有一一对应的转换关系,转换过程会与显示器设置、印刷油墨设置以及分色设置有关。
在处理图像时,一般不采用 CMYK 模式,因为:①这种模式的图像文件占用的存储空间较大;②色域范围比 RGB 小得多。

亮度
亮度表示某种颜色在人眼视觉上引起的明暗程度,它由光的强度(能量)决定:光的强亮越大,景物就越亮;光的强度越小,景物就越暗。
对于灰度图象而言,亮度就是图像的灰度值。
色调
色调(色相)表示光的颜色,它由光的波长决定。例如自然界中的七色光就分别对应着不同的色调,每种色调分别对应着不同的波长。
在通常的使用中,色调是由颜色名称标识的,比如红、橙或绿色。
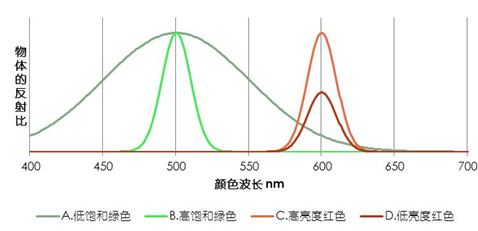
饱和度
饱和度指颜色的纯度(鲜艳程度),它由主波长的纯光谱色与白光的比例决定,也就是说,夹杂白光的多少。越接近光谱色、白光比例越小,则饱和度越高,色彩越鲜艳醒目;距离光谱色越远、白光比例越大,饱和度越低,色彩越平淡晦暗,越不鲜艳。 如对白光来讲,它的色饱和度为 0(没有色彩),纯色的色饱和度是 100%,指该彩色中不含白光。
HSI 色彩模型
最直观的色彩描述方法。用色调(Hue)、色饱和度(Saturation)和亮度(Intensity)来描述色彩。它与人类颜色视觉感知非常接近,但独立于设备(设备造不出来,仅存在于软件中)。
这个模型有两个特点:I 分量与图像的彩色信息无关;其二,H 和 S 分量与人感受颜色的方式是紧密相连的。这些特点使得 HSI 模型比 RGB 色彩空间更符合人的视觉特性,非常适合于借助人的视觉系统来感知彩色特性的图像处理算法。
LAB 色彩模型
一种能够描述颜色感觉的标准语言,能够用数学方法唯一精确定义颜色刺激所产生的感觉,这种模型就是 LAB 模型。
L 表示亮度,A 赋予了从红到绿的所有颜色,B 赋予了从黄到蓝的所有颜色,该模型覆盖了全部的可见光色谱。
该模型与设备无关(仅存在于数学 / 软件中)。 没有提供直接显示的格式,必须要转换到其它色彩空间来显示。
 .
.