编程与调试 -- 深度学习 Note

同为半精度，BF16 和 FP16 有什么区别？

浮点数由 3 部分组成

• 符号 位 S：表示数据正负
• 指数位 E ：指数位代表可表示的数值范围，位数越多可表示数据的范围越大
• 尾数位 M：就是有效数字，位数越多可表示数据的精度越高

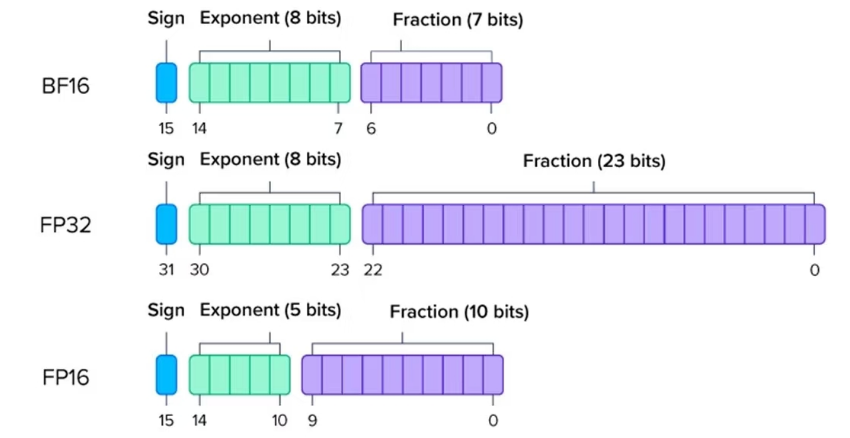
• 以 FP16 为例，1 位符号 + 5 位指数 + 10 位尾数 = 16 位
• 以 BF16 为例，1 位符号 + 8 位指数 + 7 位尾数 = 16 位
• 以 FP32 为例：1 位符号 + 8 位指数 + 23 位尾数 = 32

位这使得：

• BF16 可表示数据的范围更大（与 FP32 一样，8 位指数），而 FP16 范围较小
• FP16 精度更高，BF16 精度较低
• FP32 与 BF16 可表示的数据范围一致

为什么现在 BF16 更受欢迎？

• 训练稳定性：由于保持了 FP32 的数值范围，BF16 在反向传播时梯度更稳定，不太需要额外的 loss scaling（损失缩放）等技巧
• 硬件友好：BF16 可以直接转换到 FP32（只需补 0），计算效率更高
• 计算速度快：浮点数乘法和除法的能耗与尾数长度的平方成正比，所以 BF16 在运算速度上有天然优势
• BF16 与 FP32 兼容性好：从 FP32 转换为 BF16 只需截断尾数，而 FP16 转 BF16 需处理溢出问题

值得准备的题目

• Debug Transformers。这是经典题型之一：你会拿到一个有问题的自注意力模块实现，需要进行调试。一定要练习调试张量的形状，并特别注意因果注意力掩码（causal attention mask），这里是最容易出错的地方；
• Top-k /kNN。选出前 k 个最大元素的问题在机器学习的很多场景中都会出现，非常适合作为面试题，尤其是因为其解法并不是能现场发明出来的东西。一定要确保你熟悉堆的概念和用法；
• 实现 BPE。Tokenizer 是大语言模型中最麻烦的部分，而不出错地实现 BPE 并不容易。这也是比较常见的考察点；
• 从头实现反向传播。包括手写自动微分、链式法则等的基础版本；
• KV Cache。本质上就是构建一个矩阵，但如果你之前没见过，可能会用一种很绕的方式来做；
• 二分查找、回溯、Dijkstra 算法等。