图像处理 -- JPEG 图像压缩原理技术
很经典的 JPEG 算法,即使在大学课堂学过,至今还恋恋不忘,偶然见到这篇文章,抄录了一遍。 1992 年提出,直到 32 年后的今天,你大爷还是你大爷,没有任何其他图像格式能跟 JPEG 抗衡。! 离散余弦变换用于图片有损压缩,简直是完美。 note

JPEG(Joint Photographic Experts Group)是 JPEG 标准的产物,该标准由国际标准化组织(ISO)制订,是面向连续色调静止图像的一种压缩标准。 JPEG 格式是最常用的图像文件格式,后缀名为 .jpg 或 .jpeg。
前言
从事各行各业的大佬们,我相信,你们对图像格式是不陌生的,有很多种图像格式,比如,png,jpeg 等等,但是你发现, 同一张图片,当我们把他用工具变成各种其他格式时,其在计算机文件系统显示的文件大小各不一样,但是当你打开显示时, 从视觉角度上看,几乎看不出差距。那为什么现实的文件大小不一样,但是带给我们的视觉感受确实几乎一样的呢, 这里面就涉及到一个领域:数据压缩,具体到图像这块称之为图像压缩技术。 今天,我就来给大家简单讲讲我们常用的 JPEG 压缩原理技术。
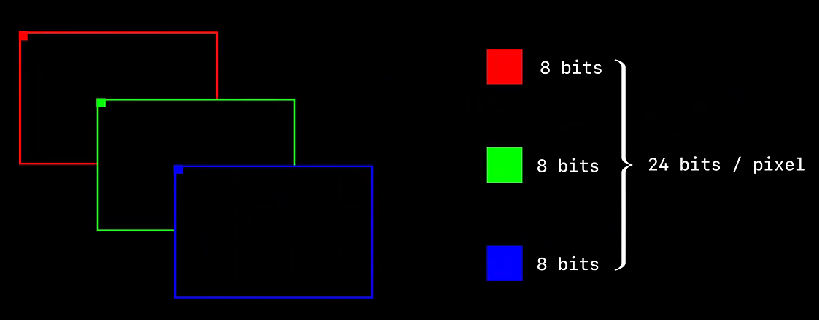
我们知道,常见的图像是由 RGB 格式组成,图像上的每个像素值分别由 R(8bit)G(8bit)B(8bit) 表示,如下图所示:
下面展示的是一张 2592x1944(所谓的 2K 分辨率)图像,在没有经过任何压缩和利用 JPEG 技术后的文件大小:
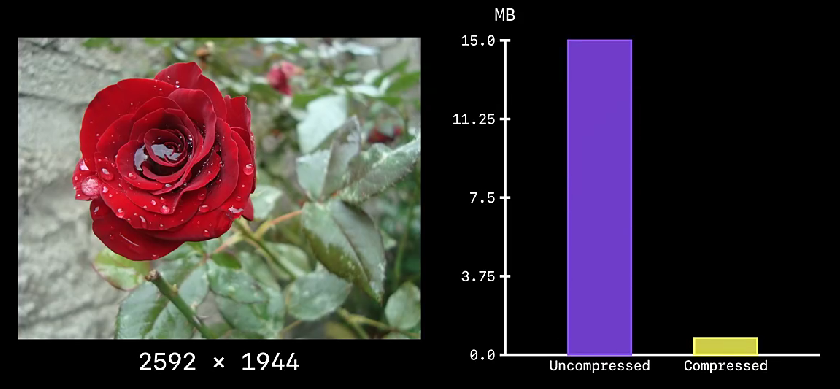
压缩前大约 15M,压缩后大约只有 0.8M。
压缩技术一:颜色空间转换
研究人员通过大量实验证明,人类视觉系统对亮度的更敏感,而对颜色没那么敏感,如下图所示,A 和 B 其实是一种颜色。

因此,我们可以将图像从 RGB→YCrCb 空间(Y:亮度,Cb:蓝色色度,Cr:红色色度),缩减 Cr 和 Cb 分量的采样数,而对于亮度 Y,则保留 0~255 等级,这个技术就叫做色度下采样,更常见的称呼是色度抽样。

未对 Cr 和 Cb 进行下采样

对 Cr 和 Cb 进行下采样
我们来具体看看一个例子,下图是一副 8x8 的图,将其 YCrCb 单独分离出来:
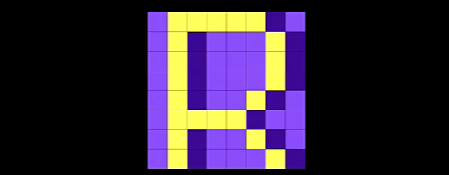
YCrCb 空间
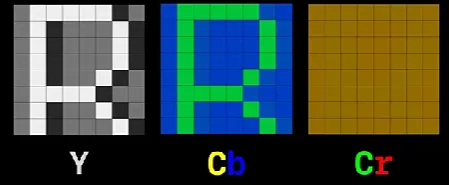
然后我们分别对 Cr 和 Cb 进行下采样操作(2X2 窗口滑动,取左上角元素):
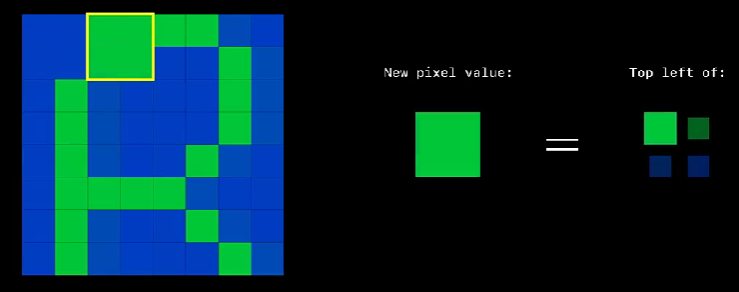
对 Cr 进行下采样,Cb 也进行同样的操作
最终得到如下:

下采样的 YCrCb 空间
然后合并得到:
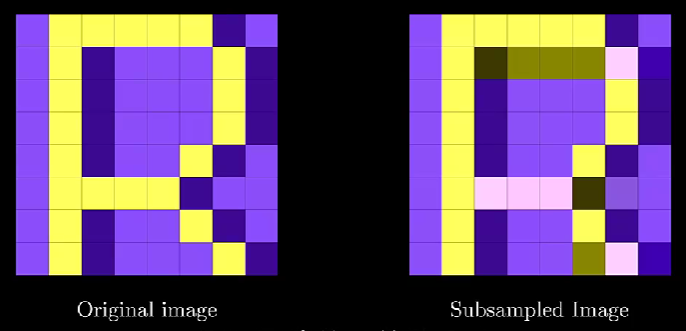
未进行下采样和进行下采样的图
上述过程进行对图像进行色彩下采样操作,再来看看对于 2k 的图,进行色彩下采样操作后的前后对比:

原图像(未经压缩)和被压缩后的图像
通过上述操作,我们可以看出,相对于原图,我们压缩了 50% 的存储空间:

图像数据在压缩了接近 50% 之后,对于人类视觉系统而言,也几乎没有什么差距,但是 JPEG 压缩技术可以做到接近 95% 的压缩,那还能从哪些地方进行数据压缩呢?
压缩技术二:DCT 2D 变换
从信号处理角度看,数字图像其本身就是一种信号,那可不可以从这个角度剖析图像自身蕴含的信号,进一步抽取我们尽可能需要保留的信息,而去除一些无关紧要的其他信息呢?答案是肯定的。首先我们抽取图像的一行,
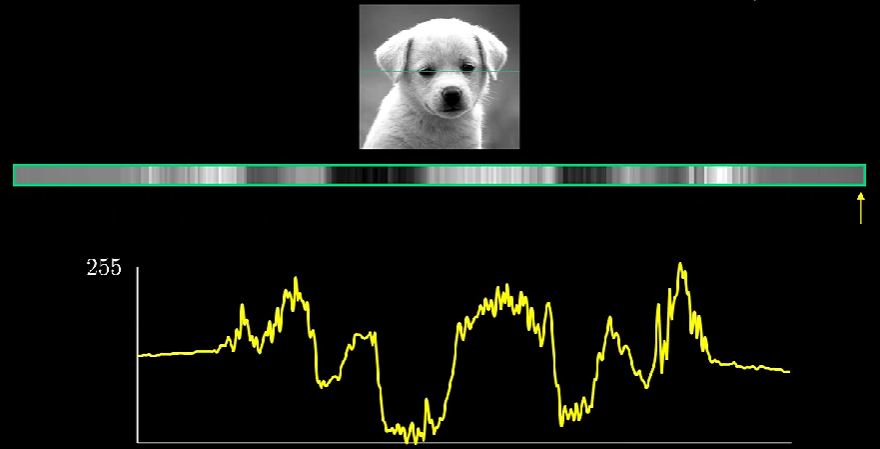
图像的一行所蕴含的信号图像
通过大量的视觉实验,我们知道,人类视觉对高频信息并不那么敏感:
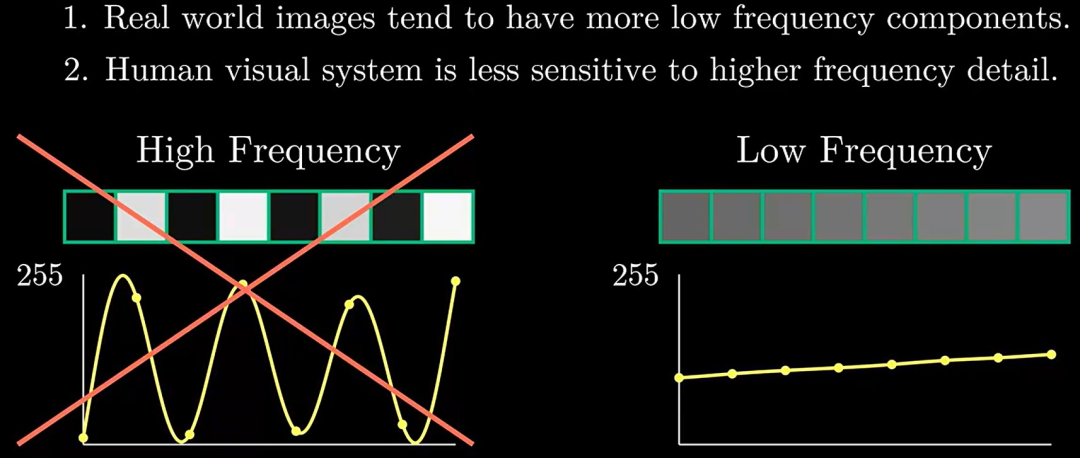
人类视觉对高频信息并不敏感
可以利用信号处理领域的相关手段,分析出图像中高低频信息含量,并通过一定手段筛选出我们需要的信息。此时,一个重要的方法排上了用场,DCT( 离散余弦变换 ),在冈萨雷斯的《数字图像处理》书中,有详细的推理,这里简述一下精髓:一切信号都可以用若干不同频率的标准余弦信号通过特定的组合形式表示出来。考虑下面一个只有 8 个像素的单行图像:
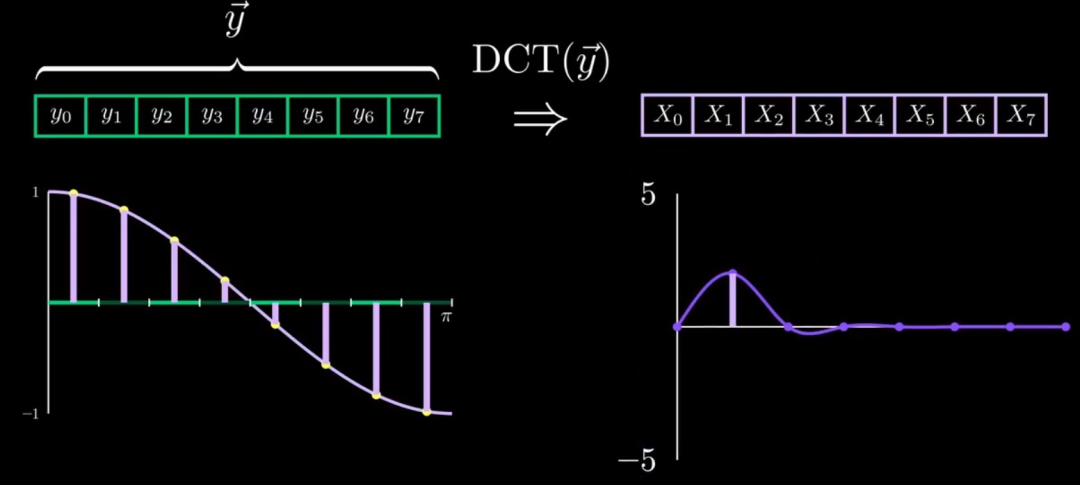
cos(x)
从上面可以看出,对于 y0~y7,这 8 个离散值从标准的 cos(x) 函数上采样获取。也就是说,对于 y 来说,其可以只用一个 cos(x) 就能完全表达,因此,通过 DCT 变换后,在幅频图上,对于 cos(x) 的那个系数 X1=1, 而其他 X0, X2, ….., X7 则为 0(X0~X7 分别代表从低频信号(比如 cos(x))到高频信号(比如 cos(7x))的系数), 同理有,当 y0~y7 服从 cos(2x) 时,其经过 DCT 变换后,其 X2=1, 下图是将 y 值在 0~255 范围空间进行转换到-128~128 空间。
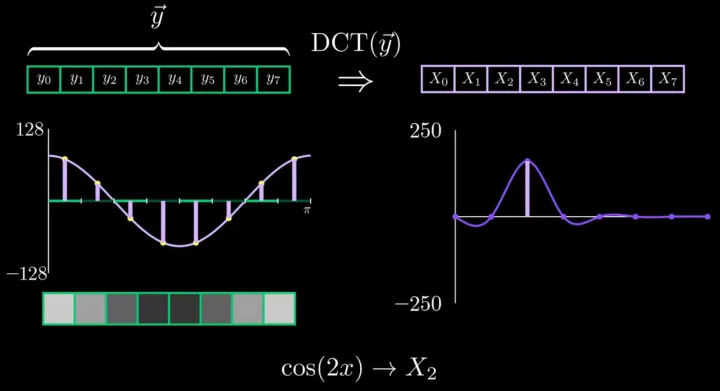
cos(2x)
类似的有,对于 y0~y7 从 cos(3x) 进行下采样操作,对应的 DCT 变换后的的幅频图。
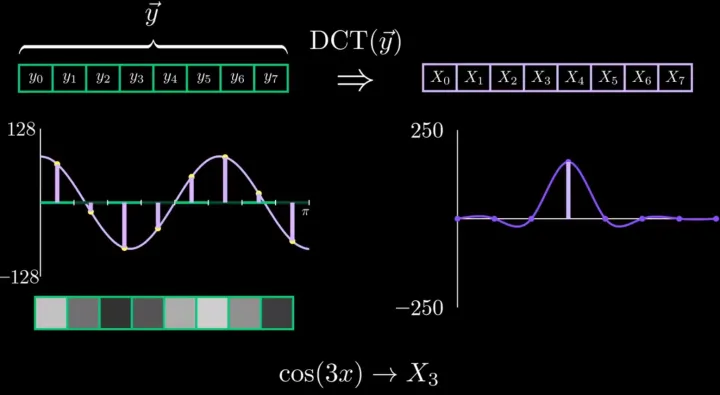
cos(3x)
因此,经过上述分析,就有:cos(kx) 与 Xk 一一对应的关系:
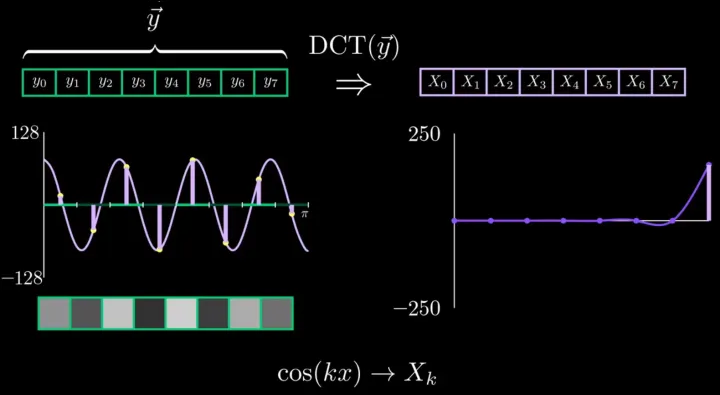
cos(kx)
枚举所有情况,如下所示:
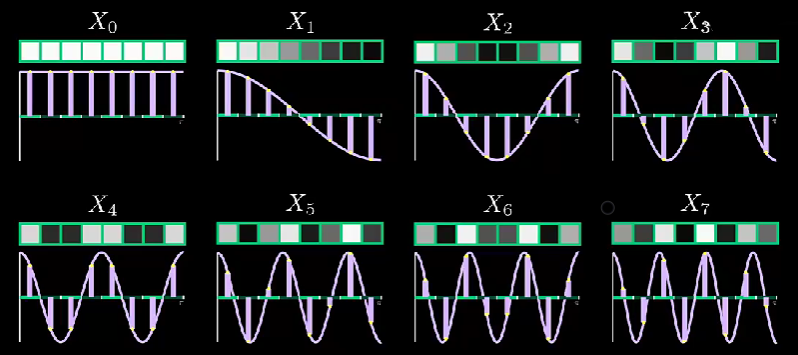
因此,我们也可以得到:8 个像素值的所有组合,均可以表示为该 8 个余弦函数的总和。这里我们分析一下,对于任意的 8 个像素值组合,其对应的下面的 DCT 变换如下,其 Xk 求解形式如下:
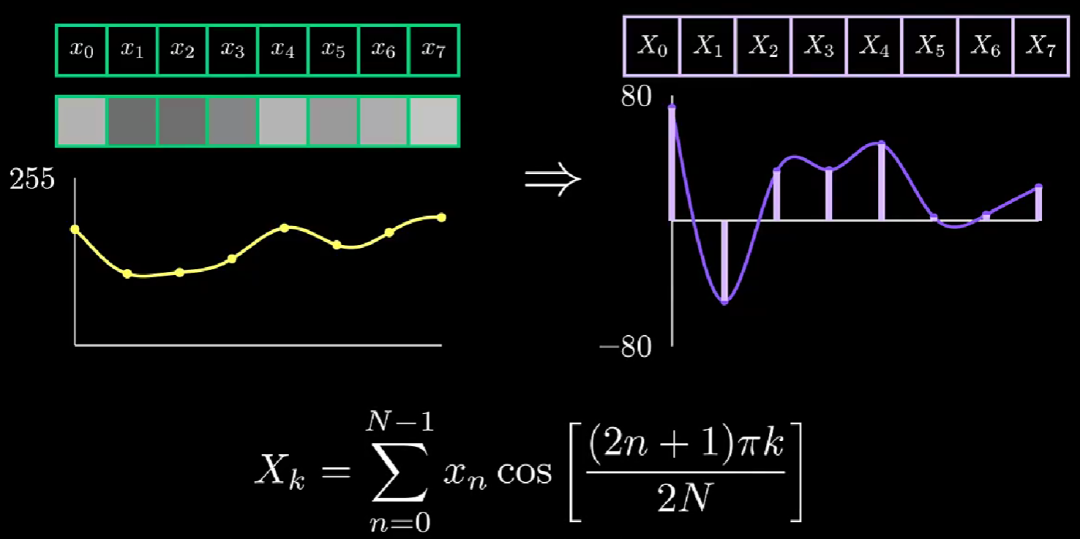
将其写成向量形式有:
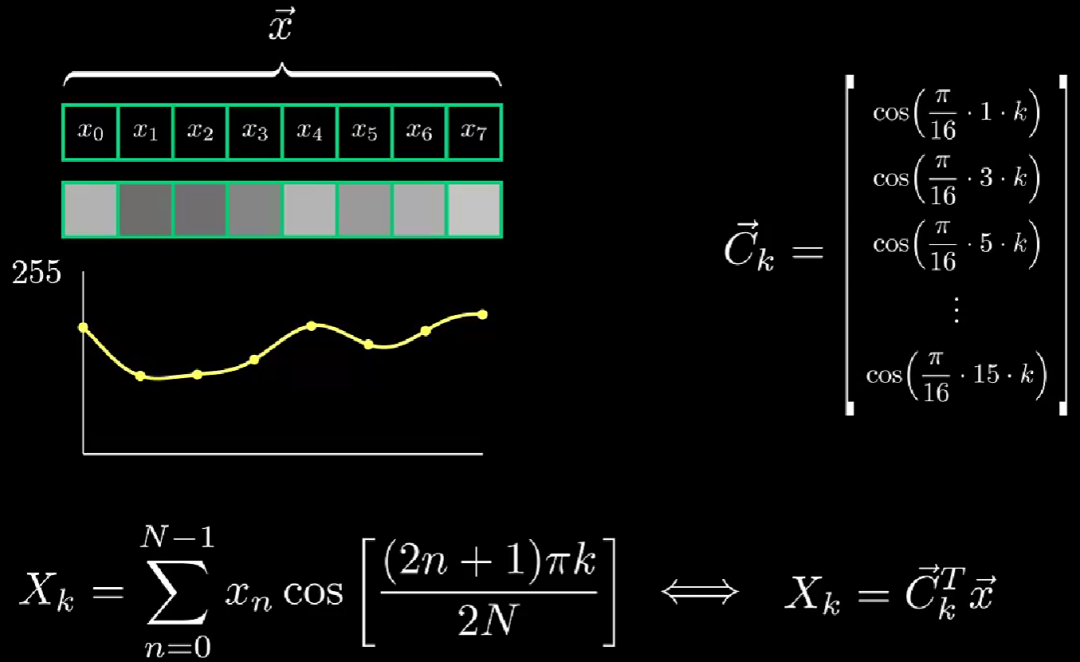
更进一步有:
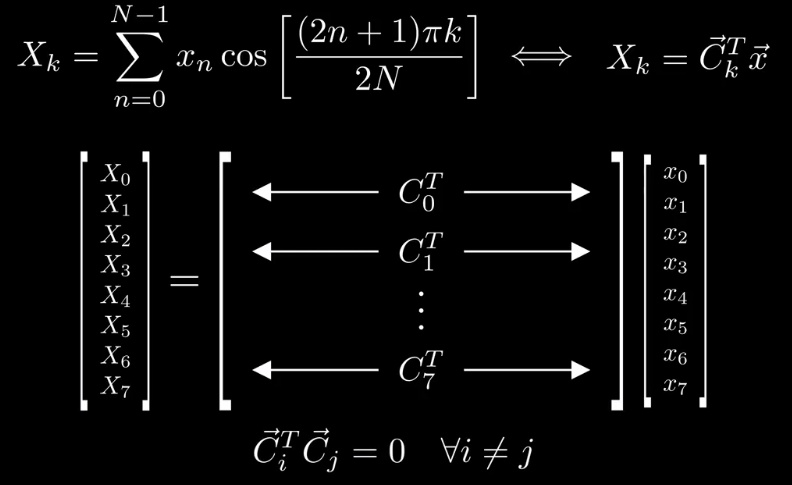
需要注意的是,DCT 变化是可逆的,对应如下图所示:
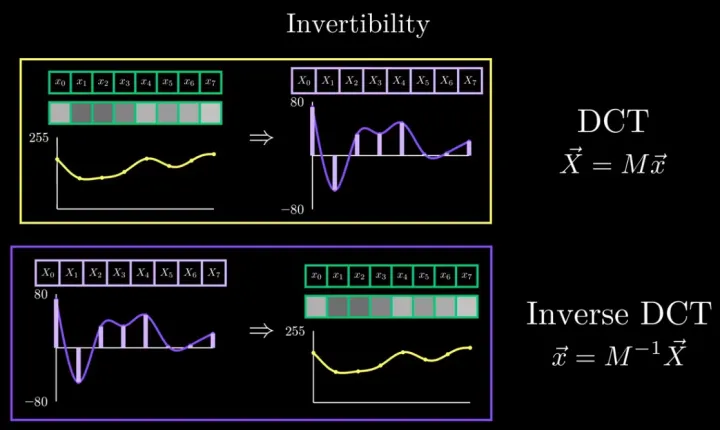
我们将 Inrerse DCT 拆开写,更清楚的显示任意信号和对应的标准余弦信号组合关系:
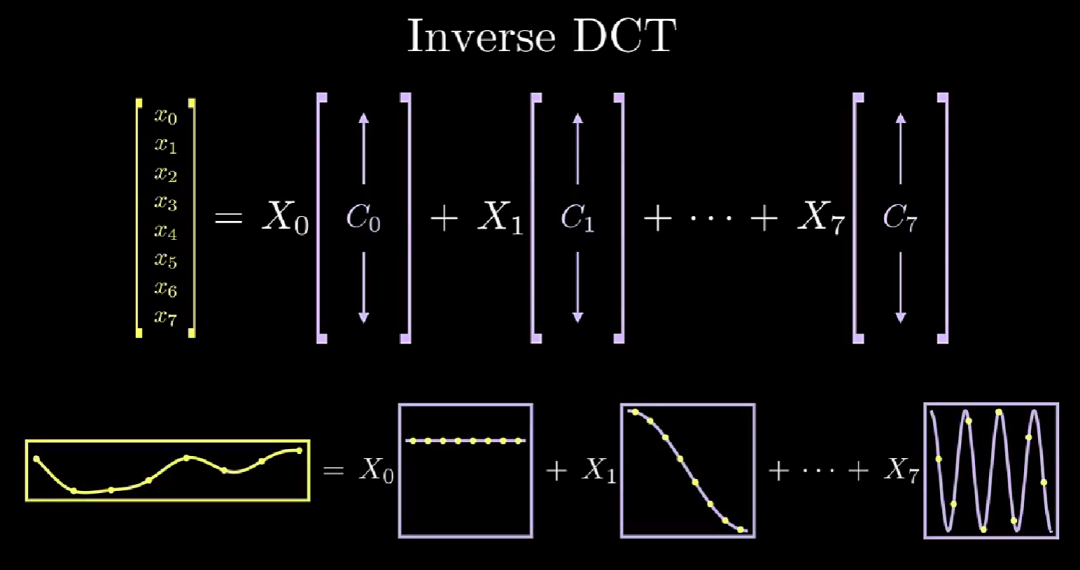
接下来,我们从图像中,任意扣取一个 8x8 的区域进行分析,此时,一维的 DCT 变换也随之拓展到二维:
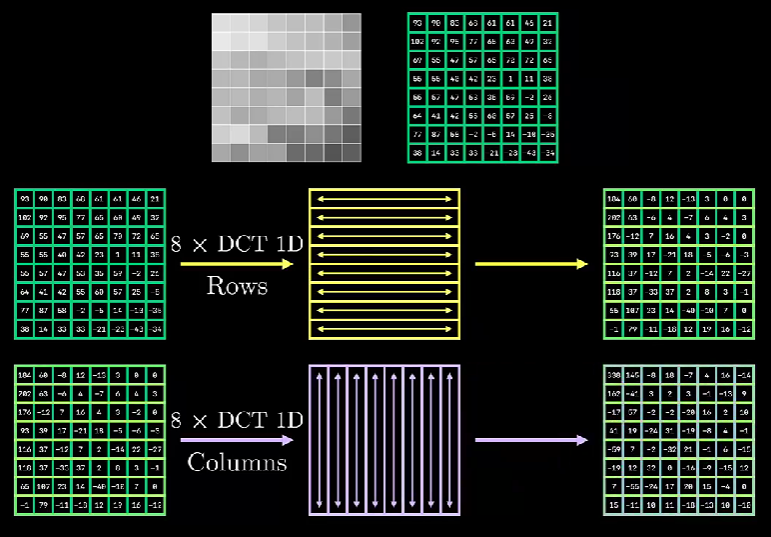
DCT 2D 变换
由于 DCT 具有可逆性,也就是说,根据 DCT 2D 得到的变换矩阵,我们可以完整反推出对应的像素值,我们可以把 64 个系数从低频到高频依次加入,其图像的变换情况:
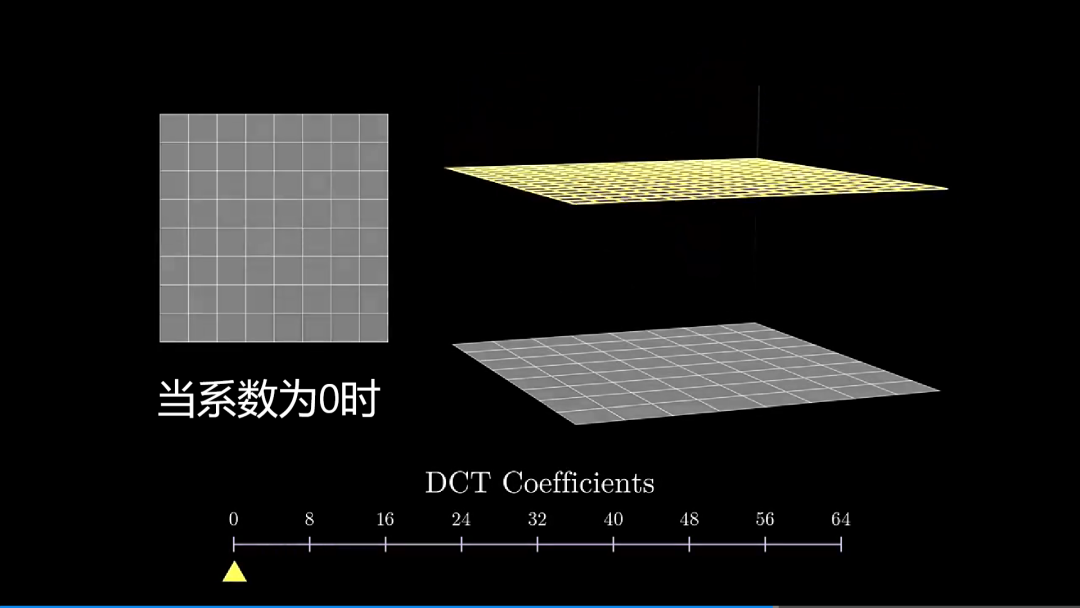
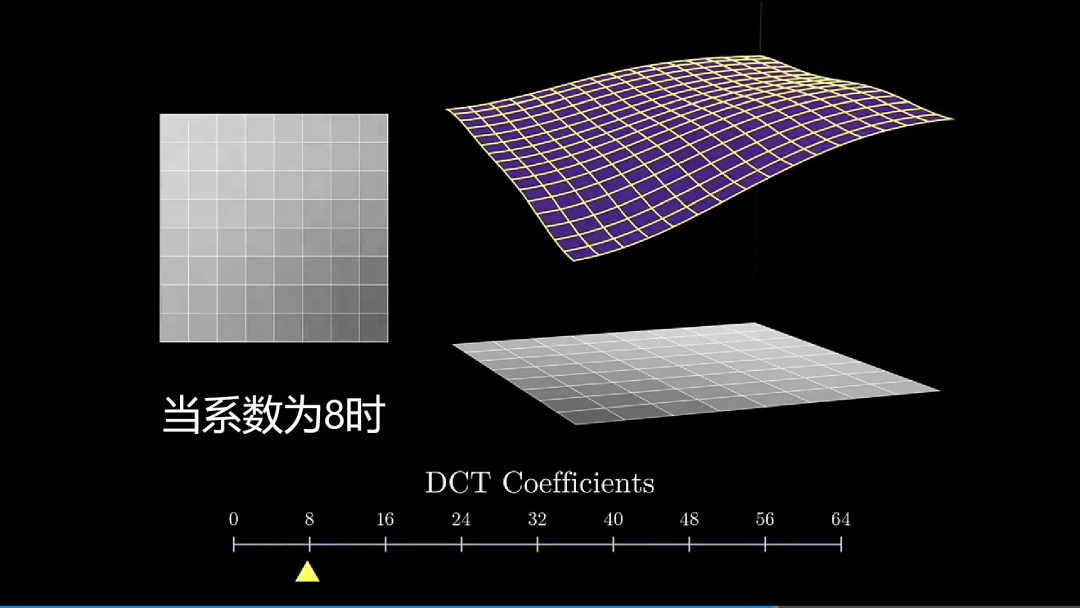
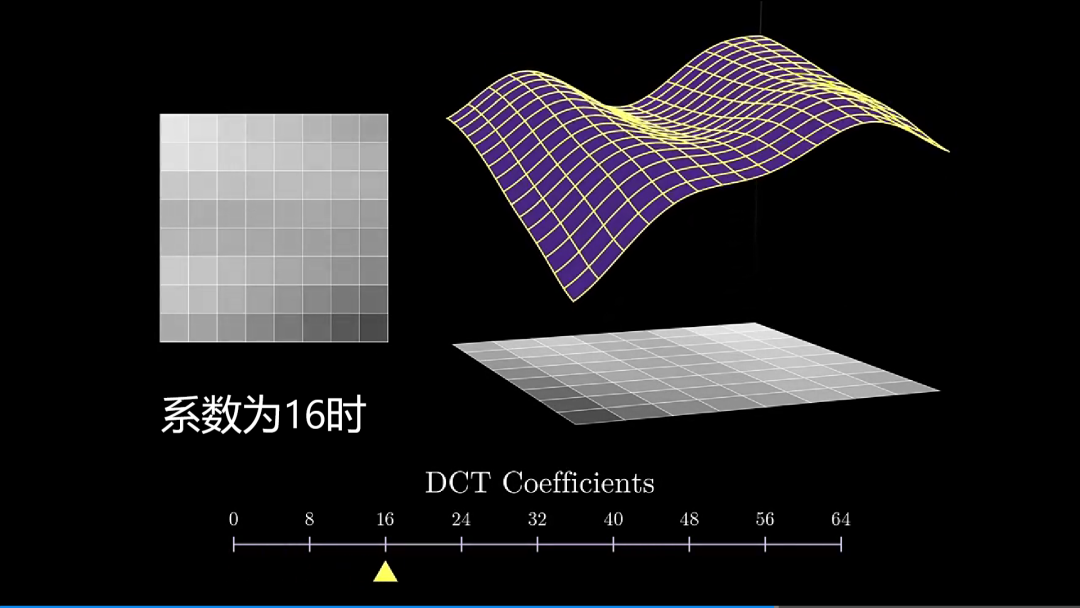
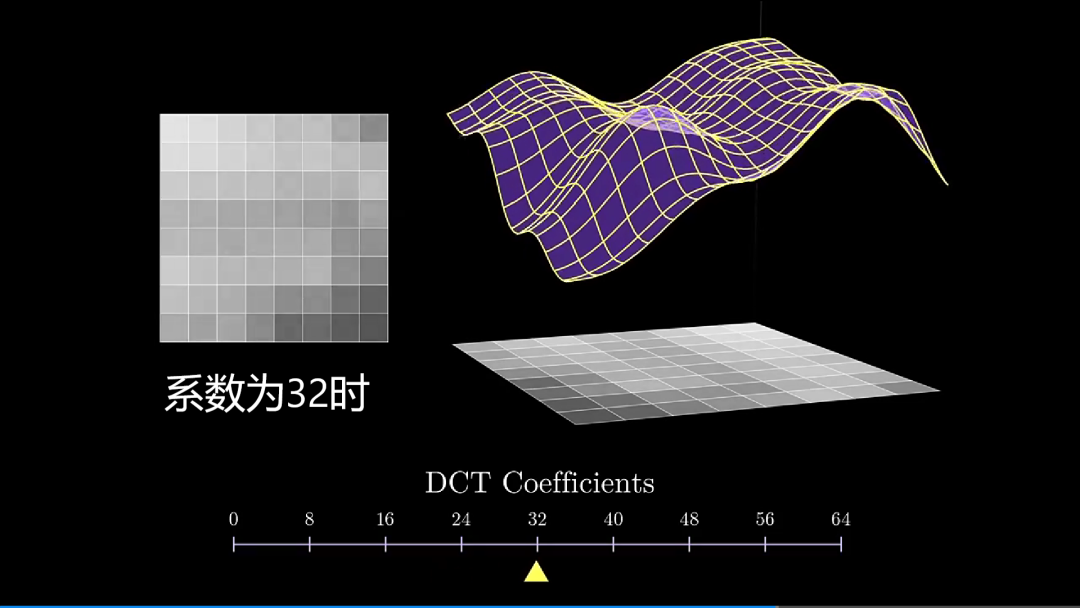
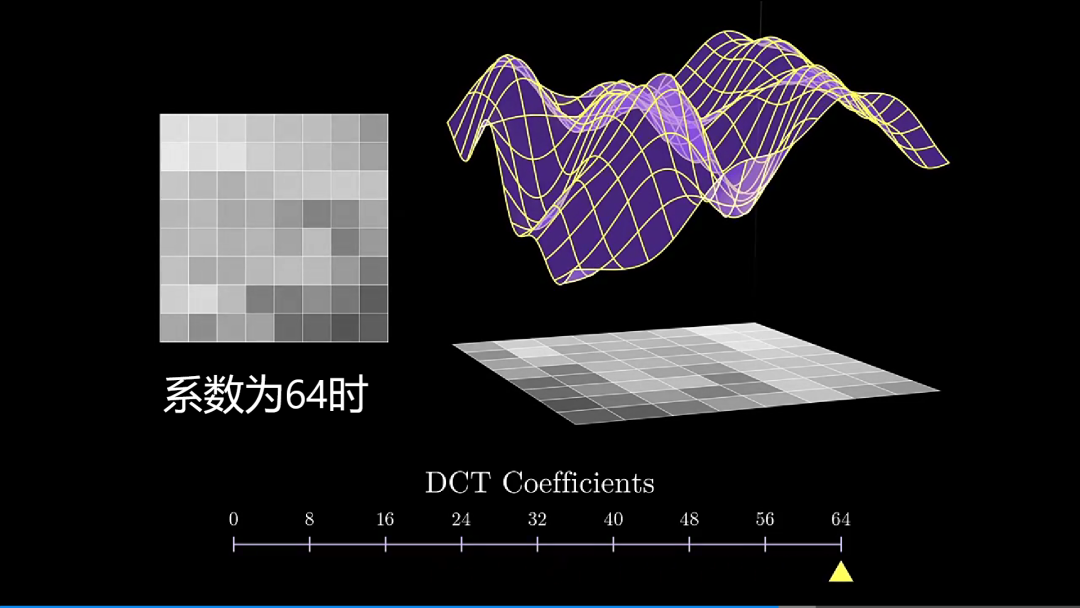
从上述变换可以看出,后面添加的一些高频信息,对图像的整体改变并没有变多少,这是发生一些非常细微上的表现,然而,我们人类视觉系统对这些改变并不敏感。
在 JPEG 算法中,图像被分为了 8*8 的像素组,每个像素组用自己的离散余弦变化进行频域编码。为什么选用 8*8 的像素组。采用比 8*8 更大的像素组,会大幅增加 DCT 的运算量,且编码质量也不会明显提升;采用比 8*8 更小的像素组会导致分组增多降低精度。所以 8*8 的像素组是效率最优的结果。对每个像素组组,我们都用上述 DCT 进行变换。
下面演示不断添加频率个数,图像恢复情况:





当系数为 0 时,恢复出来一片白板;只用一个系数时,图像大体轮廓已出现;加入 8 个频率时,图像基本上恢复出原样;加入 16 个频率时,图像越来越清楚。随着后续高频不断加入,图像并没有多大改变,此时,我们就可以丢弃 DCT 的高频分量了。
具体怎么丢弃呢?研究人员通过大量的视觉实验,最终定义出一个量化表格(Quantization Table),如下所示:
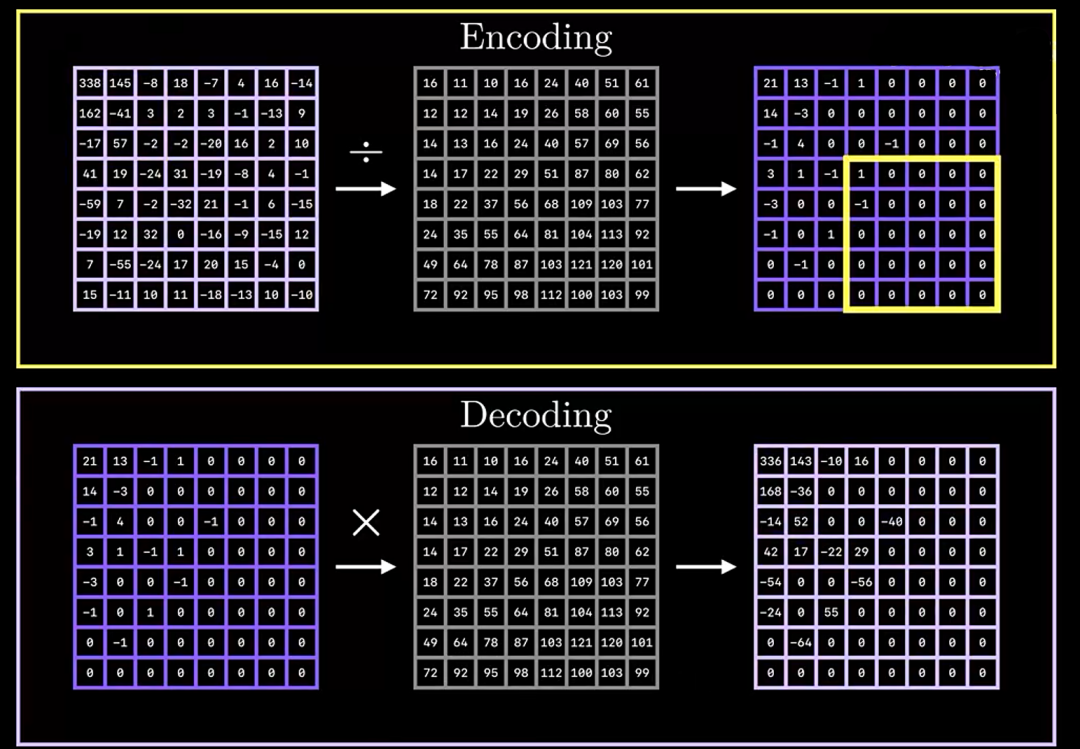
Quantization Table
将 DCT 2D 变换得到表格(上面 Encoding 中左边)与量化表格进行逐元素触发,得到右边蓝色表格, 可以发现,变成一个稀疏矩阵,同时,也注意到一个事情,如下图所示,DCT 2D 得到的系数矩阵, 其左上角最大,低频信息集中在左上角区域,而高频部分则集中在右下角部分(低频信息,对应的 DCT 系数矩阵其能量系数也大)。这个性质其实可以从 DCT 2D 的推理过程可以得到。在上述经过量化后的系数矩阵中,右下部分出现大量的 0,也就意味着,该信号可以被舍弃。注意,舍弃高频信息的过程就是量化过程,这里会出现信息损失。
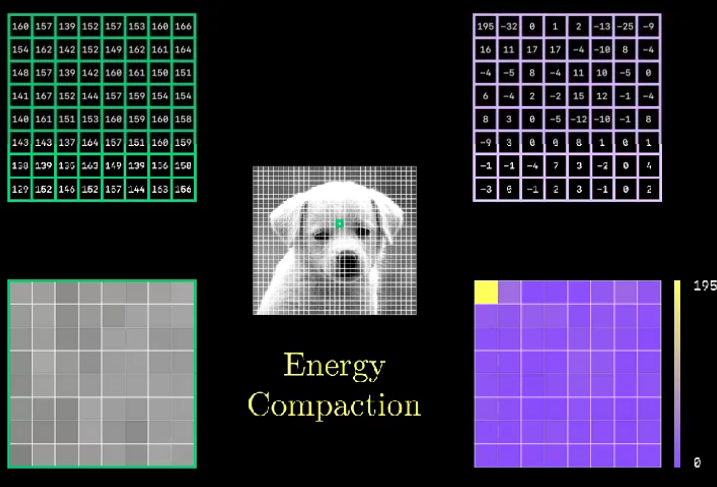
JPEG 压缩技术规定了不同 quality factor 下的量化值,QF 越大,量化表格里的数值就越小,其损失也就越小,同时,结合人眼对色彩的敏感要低于亮度,因此,对于 Y 和 CrCb, 定义了不同的量化系数。

为了进一步对数据进行压缩,我们对经过量化后的稀疏矩阵进一步分析,采用游程编码 (ZigZag) 和霍夫曼编码组合手段,进一步减少信息存储,如下图所示:

ZigZag 游程编码 +Huffman 编码
最后,对压缩信息进行 huffman 编码处理,如下图所示:
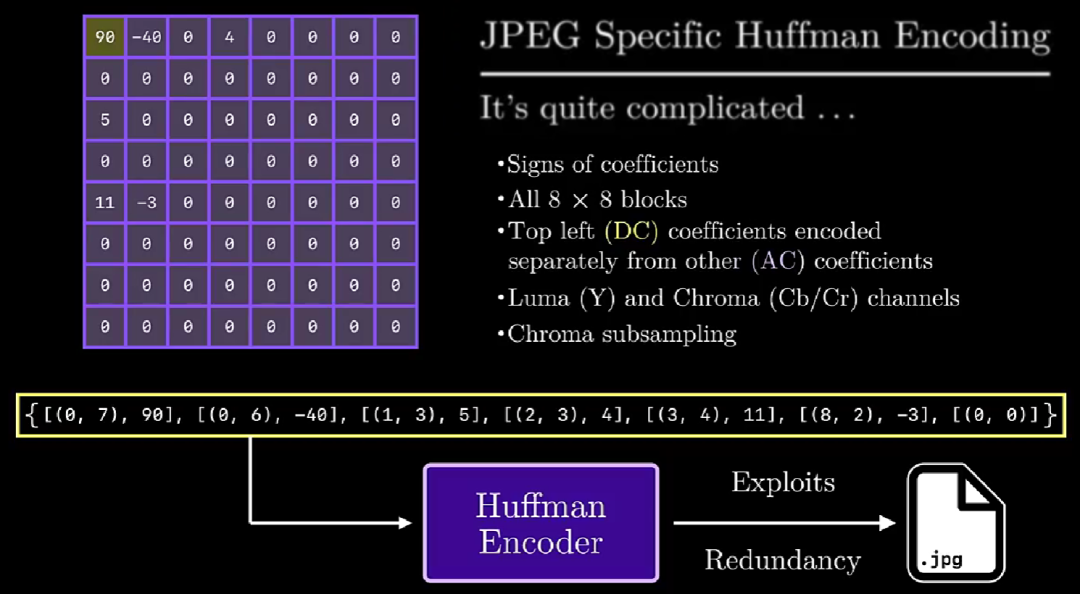
ZigZag 游程编码 +Huffman 编码
上述整个过程中,就是 JPEG 图像压缩原理,整个过程清晰明朗,一气呵成,希望能帮助到各位。
总结
JPEG 图像压缩技术原理其核心技术包括以下两个方面:
- RGB to YCrCb:利用人类视觉系统对色彩的不敏感特性,对 Cr 和 Cb 下采样;
- DCT 2D 变换:利用人类视觉系统对高频的不敏感特性,舍弃部分高频信息,采用游程编码和 Huffman 编码技术,进一步减少数据冗余。
参考视频源出处: https://www.youtube.com/watch?v=0me3guauqOU 中文字幕视频解说: https://www.zhihu.com/question/39689253/answer/2490557388
参考资料快照

 .
.