图形学笔记 -- 3D 引擎数学:线性代数
程序员的数学:线性代数。机器学习以及计算机图形图像学的数学基础。
那么我们可以制作一个视角(我们毕竟使用三个维度)矩阵代码:
template<typename T>
Matrix4x4<T> perspective(T fovy, T aspect, T near, T far){
T q = 1.0f / tan((0.5f * fovy) * (3.14 / 180));
T A = q / aspect;
T B = (near + far) / (near - far);
T C = (2.0f * near * far) / (near - far);
return Matrix4x4<T>(
Vector4<T>(A,0,0,0),
Vector4<T>(0,q,0,0),
Vector4<T>(0,0,B,-1),
Vector4<T>(0,0,C,0));
}
01 课
从字面理解什么是线性代数
\[\left\{ \begin{alignedat}{2} &x \space- \space&2&y \space=\space 1 \\ 3&x \space+ \space&2&y \space=\space 11 \end{alignedat} \right.\]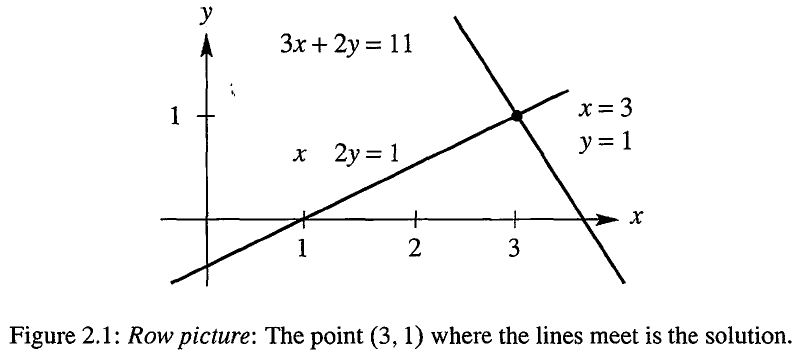
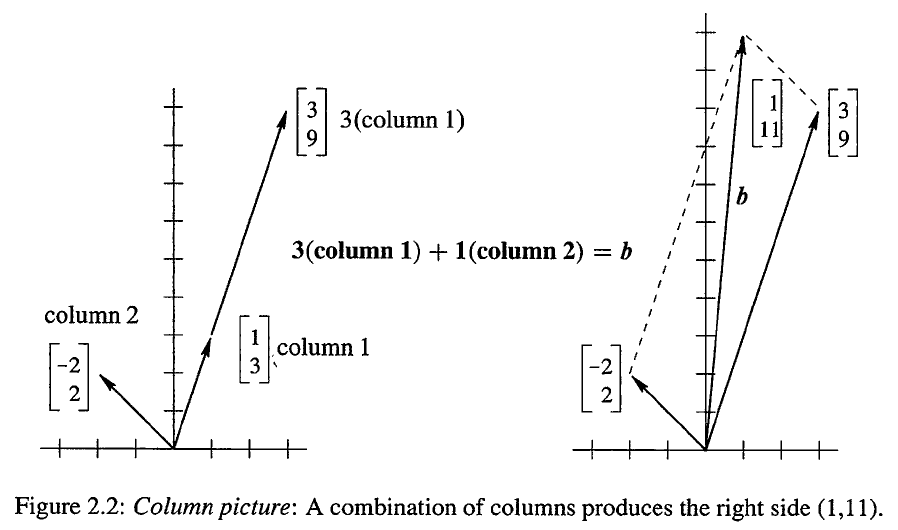
向量和矩阵
向量的长度与单位向量
内积与向量的方向
内积(点积、点乘或数量积)投影变换:多维空间投影到一维空间。
向量的点乘,也叫向量的内积、数量积,对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,点乘的结果是一个标量。
\[a=\left[a_{1}, a_{2}, \ldots a_{n}\right]\] \[b=\left[b_{1}, b_{2}, \ldots b_{n}\right]\] \[a \bullet b=a_{1} b_{1}+a_{2} b_{2}+\ldots+a_{\mathrm{n}} b_{n}\]几何意义
可以用来表征或计算两个向量之间的夹角,以及在 $b$ 向量在 $a$ 向量方向上的投影。
根据这个公式就可以计算向量 $a$ 和向量 $b$ 之间的夹角。从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系。
\[a \bullet b=|a| \ |b| \cos \theta\]正交向量
叉乘
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
\[\begin{array}{l} a=\left(x_{1}, y_{1}, z_{1}\right) \\ b=\left(x_{2}, y_{2}, z_{2}\right) \end{array}\] \[a \times b=\left(y_{1} z_{2}-y_{2} z_{1},-\left(x_{1} z_{2}-x_{2} z_{1}\right), x_{1} y_{2}-x_{2} y_{1}\right)\]几何意义
在三维几何中,向量 $a$ 和向量 $b$ 的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于 $a$ 和 $b$ 向量构成的平面。
在 3D 图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于 a,b 的法向量,从而构建 X、Y、Z 坐标系。
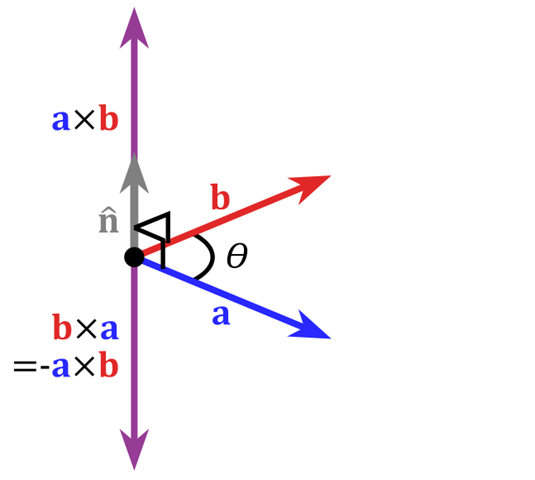
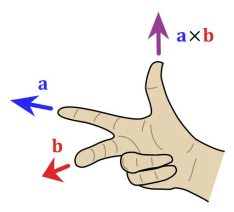
在二维空间中,叉乘还有另外一个几何意义就是:axb 的模等于由向量 $a$ 和向量 $b$ 构成的平行四边形的面积。
\[| \vec a \times \vec b | = |\vec a| \cdot |\vec b| \cdot \sin \theta\]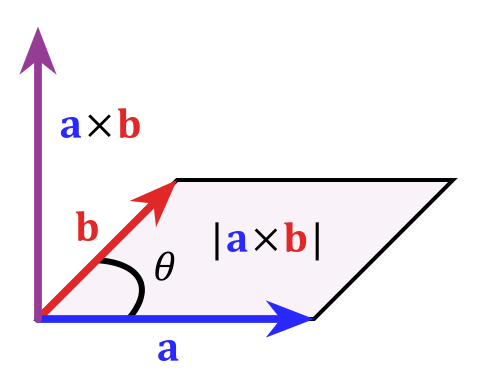
点乘内积叉乘外积比较
矩阵乘法
矩阵和向量的乘积鸡兔同笼
零矩阵
02 课
方阵对角矩阵单位矩阵逆矩阵
高斯若尔当消元法解方程求逆矩阵
用矩阵描述消元过程
置换矩阵
消元法的本质
LU 分解
在线性代数中, LU 分解(LU Factorization)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积)。 LU 分解主要应用在数值分析中,用来解线性方程、求反矩阵或计算行列式。
基底
基变换
矩阵的乘法的几何意义就是空间变换。
线性组合线性相关线性无关生成空间
二维行列式
03 课
三维行列式
行列式的计算:代数余子式
通过伴随矩阵求逆矩阵
矩阵运算练习
奇异矩阵
线性子空间
零空间
子空间的基于线性无关
列空间零空间练习
行空间右零空间
04 课
图和网络
ImA 与 KerA
n 大于 m 的情况
m 大于等于 n 的情况
原像
原像练习
正交子空间
复习:AX=b 总结
A 转置 A
投影到直线
05 课
投影到平面
e 是 b 在零空间的投影
最小二乘法
最小二乘法结果分析
标准正交基
正交矩阵
标准正交基下投影到子空间
Gram-Schmidt 格拉姆-施密特正交化
三维里沿着 x 轴旋转
格拉姆-施密特正交化例子 2
06 课
特征值特征向量几何含义
特征向量特征值求解
特征值特征向量性质
对角化
斐波那契数列解法 1
斐波那契数列解法 2
微分方程
微分方程 2:解耦和
微分方程 3:矩阵指数
07 课
马尔可夫矩阵转移概率矩阵
三阶微分方程实例
从线性代数角度看傅里叶级数
对称矩阵
References
- [1] 程序员的数学:线性代数

- [2] 3Blue1Brown 【官方双语 / 合集】线性代数的本质 - 系列合集
- [3] 3D 数学,矩阵简介
参考资料快照
- https://www.zhihu.com/question/21082351
- https://www.cnblogs.com/seniusen/p/9959535.html
- https://zhuanlan.zhihu.com/p/49820858
- https://zhuanlan.zhihu.com/p/92274158
- https://blog.csdn.net/dcrmg/article/details/52416832
- https://www.cnblogs.com/zzdyyy/p/7643267.html
- https://ke.qq.com/course/411603
- https://www.bilibili.com/video/av6731067
- https://riptutorial.com/zh-CN/opengl/example/14159/%E7%9F%A9%E9%98%B5%E7%AE%80%E4%BB%8B
参考资料快照

 .
.