机器学习笔记 -- 数学×梯度（Gradient）与梯度下降法（Gradient Descent）

Posted on September 3, 2020 (珠海)
机器学习

前言

提到梯度，就必须从导数（derivative）、偏导数（partial derivative）和方向导数（directional derivative）讲起，弄清楚这些概念，才能够正确理解为什么在优化问题中使用梯度下降法来优化目标函数，并熟练掌握梯度下降法（Gradient Descent）。

概念	物理意义
导数	函数在该点的瞬时变化率
偏导数	函数在坐标轴方向上的变化率
方向导数	函数在某点沿某个特定方向的变化率
梯度	函数在该点沿所有方向变化率最大的那个方向

导数

导数与微分：

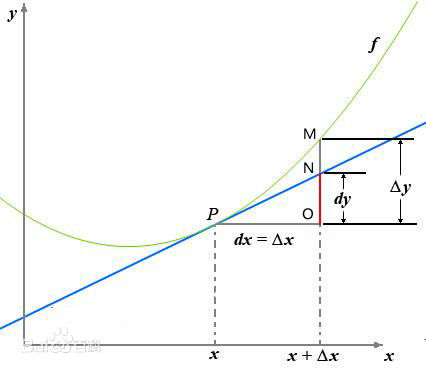
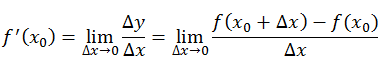
$Δx$：$x$ 的变化量；
$dx$：$x$ 的变化量 $Δx$ 趋于 $0$ 时，则记作微元 $dx$；
$Δy$：$Δy=f(x0+Δx)-f(x0)$，是函数的增量；
$dy$：$dy=f’(x0)dx$，是切线的增量；
当 $Δx→0$ 时，$dy$ 与 $Δy$ 都是无穷小，$dy$ 是 $Δy$ 的主部，即 $Δy=dy+o(Δx)$。

二阶的导数 $\frac{d^2 y}{dx^2} = \frac{d}{dx} \left(\frac{dy}{dx} \right)$。

高阶无穷小的定义：如果 $lim \frac{β}{α}=0$，就说 $β$ 是比 $α$ 高阶的无穷小，记作 $β=o(α)$。

函数 $f(x)$ 在点 $x_0$ 可微的充分必要条件是函数 $f(x)$ 在点 $x_0$ 可导。

\[dy=f'(x_0)Δx\]

导数和偏导数

偏导数的定义如下：

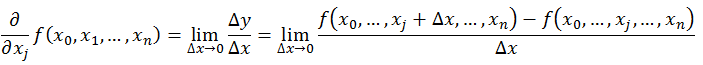
可以看到，导数与偏导数本质是一致的，都是当自变量的变化量趋于 $0$ 时，函数值的变化量与自变量变化量比值的极限。直观地说，偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。

区别在于：

导数，指的是一元函数中，函数 $y=f(x)$ 在某一点处沿 $x$ 轴正方向的变化率；
偏导数，指的是多元函数中，函数 $y=f(x_1,x_2,…,x_n)$ 在某一点处沿某一坐标轴 $(x_1,x_2,…,x_n)$ 正方向的变化率。

函数 $f$ 关于变量 $x$ 的偏导数写为 $f_{x}^{\prime}$ 或 $\frac {\partial f}{\partial x}$。偏导数符号 $\partial$ 是全导数符号 $d$ 的变体。

$f$ 关于 $x$ 的偏导数，把 $y$ 和 $z$ 视为常数，通常记为：

\[\left( \frac{\partial f}{\partial x} \right)_{y,z}\]

偏导数的几何意义

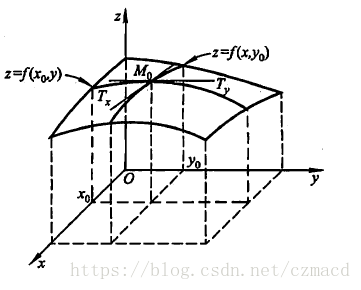
偏导数 $f_x(x_0,y_0)$ 就是曲面被平面 $y=y_0$ 所截得的曲线在点 $M_0$ 处的切线 $M_0T_x$ 对 $x$ 轴的斜率
偏导数 $f_y(x_0,y_0)$ 就是曲面被平面 $x=x_0$ 所截得的曲线在点 $M_0$ 处的切线 $M_0T_y$ 对 $y$ 轴的斜率

导数与方向导数

很多时候要考虑多元函数沿任意方向的变化率，那么就引出了方向导数。方向导数的定义如下：

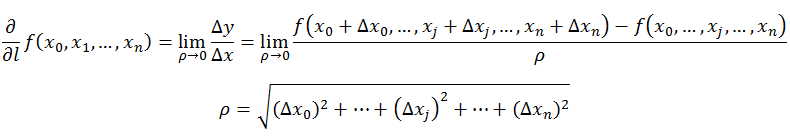
在前面导数和偏导数的定义中，均是沿坐标轴正方向讨论函数的变化率。那么当我们讨论函数沿任意方向的变化率时，也就引出了方向导数的定义，即：某一点在某一趋近方向上的导数值。

通俗的解释是：

我们不仅要知道函数在坐标轴正方向上的变化率（即偏导数），而且还要设法求得函数在其他特定方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。

导数与梯度

梯度的定义如下：

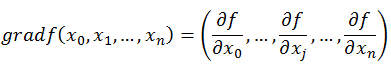
\[\nabla f(a) = \left(\frac{\partial f}{\partial x_1}(a), \ldots, \frac{\partial f}{\partial x_n}(a)\right)\]

梯度的提出只为回答一个问题：函数在变量空间的某一点处，沿着哪一个方向有最大的变化率？

梯度定义如下：

函数在某一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。

这里注意三点：

梯度是一个向量，即有方向有大小；
梯度的方向是最大方向导数的方向；
梯度的值是最大方向导数的值。

向量场

一个常见的向量场是在欧几里得空间 $R^3$ 中用单位向量 $\mathbf{\hat{i}}, \mathbf{\hat{j}}, \mathbf{\hat{k}}$ 来定义 Nabla 算子 (∇) 如下：

\[\nabla = \bigg[{\frac{\partial}{\partial x}} \bigg] \mathbf{\hat{i}} + \bigg[{\frac{\partial}{\partial y}}\bigg] \mathbf{\hat{j}} + \bigg[{\frac{\partial}{\partial z}}\bigg] \mathbf{\hat{k}}\]

或者，更一般地，对于 $n$ 维欧几里得空间 $R^n$ 的坐标 $(x_1, x_2, x_3, …, x_n)$ 和单位向量 $(\mathbf{\hat{e}_1}, \mathbf{\hat{e}_2}, \mathbf{\hat{e}_3}, \dots , \mathbf{\hat{e}_n})$：

\[\nabla = \sum_{j=1}^n \bigg[{\frac{\partial}{\partial x_j}}\bigg] \mathbf{\hat{e}_j} = \bigg[{\frac{\partial}{\partial x_1}}\bigg] \mathbf{\hat{e}_1} + \bigg[{\frac{\partial}{\partial x_2}}\bigg] \mathbf{\hat{e}_2} + \bigg[{\frac{\partial}{\partial x_3}}\bigg] \mathbf{\hat{e}_3} + \dots + \bigg[{\frac{\partial}{\partial x_n}}\bigg] \mathbf{\hat{e}_n}\]

导数与向量

导数与偏导数与方向导数是向量么？

向量的定义是有方向（direction）有大小（magnitude）的量。

从前面的定义可以这样看出，偏导数和方向导数表达的是函数在某一点沿某一方向的变化率，也是具有方向和大小的。因此从这个角度来理解，我们也可以把偏导数和方向导数看作是一个向量，向量的方向就是变化率的方向，向量的模，就是变化率的大小。

那么沿着这样一种思路，就可以如下理解梯度：梯度即函数在某一点最大的方向导数，函数沿梯度方向函数有最大的变化率。

梯度下降法

既然在变量空间的某一点处，函数沿梯度方向具有最大的变化率，那么在优化目标函数的时候，自然是沿着负梯度方向去减小函数值，以此达到我们的优化目标。

如何沿着负梯度方向减小函数值呢？既然梯度是偏导数的集合，如下：

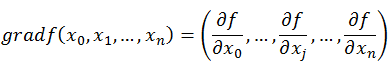
同时梯度和偏导数都是向量，那么参考向量运算法则，我们在每个变量轴上减小对应变量值即可，梯度下降法可以描述如下：

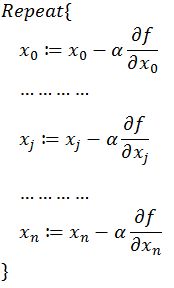
以上就是梯度下降法的由来，大部分的机器学习任务，都可以利用 Gradient Descent 来进行优化。

参考

参考资料快照

本文短链接：
If you have any questions or feedback, please reach out