MATHEMATICS -- Gabriel 喇叭,有限的体积无穷的表面积
Gabriel 喇叭

Gabriel 喇叭是 $y=1/x$ 在 $[1, +∞)$ 上的图象沿 $x$ 轴旋转一周所形成的旋转体。这个简单的三维图形有一个奇特的性质:它的表面积无穷大,却只有有限的体积。为了证实这一点,只需注意到:
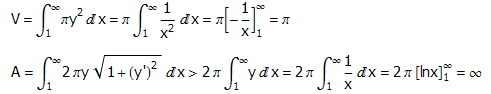
Gabriel 喇叭会导出一个非常诡异的悖论:如果你想用涂料把 Gabriel 喇叭的表面刷一遍,你需要无穷多的涂料;然而把涂料倒进 Gabriel 喇叭填满整个内部空间,所需要的涂料反而是有限的。
数学过程
双曲线 $1/x$
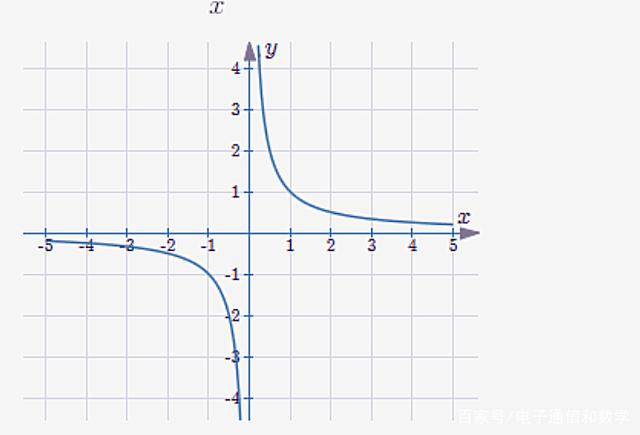
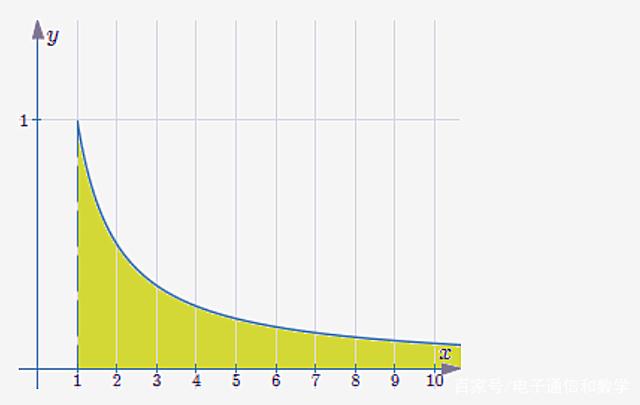
我们选择右侧部分(以避免 $x=0$ 处的不连续性)并绘制从 $x=1$ 开始的图。我们考虑虚线右侧,曲线下方和 $x$ 上方的(无限)阴影区域。
我们围绕 $x$ 轴在 $3$ 维上旋转该区域,最后得到一个(无限长的)类似角的对象。
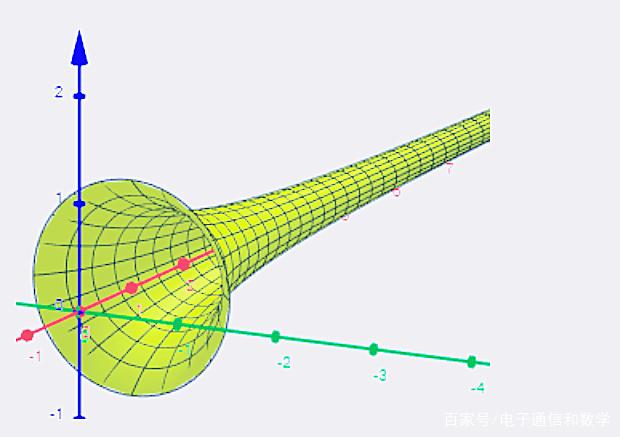
我们使用旋转体的体积公式(最基本的体积计算公式,一定要理解)
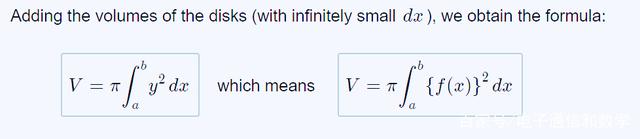
由此得到如下结果
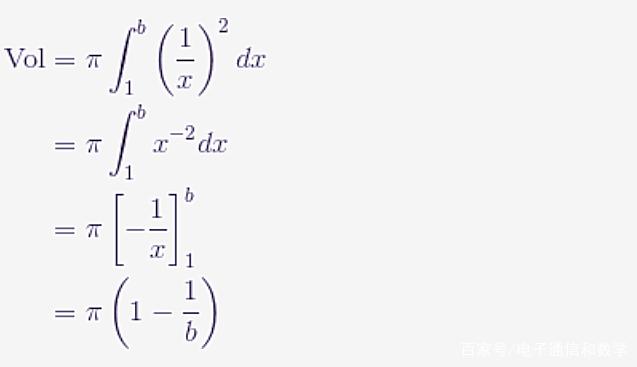
随着 $b$ 越来越大,答案中的最终分数也越来越小,因此体积为有限量 $π$,用数学符号表示为:
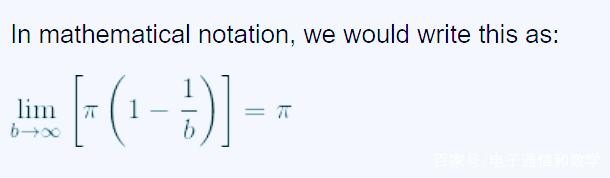
接下来,让我们考虑喇叭的表面积,旋转体的表面积计算公式为:

在这种情况下,我们有:
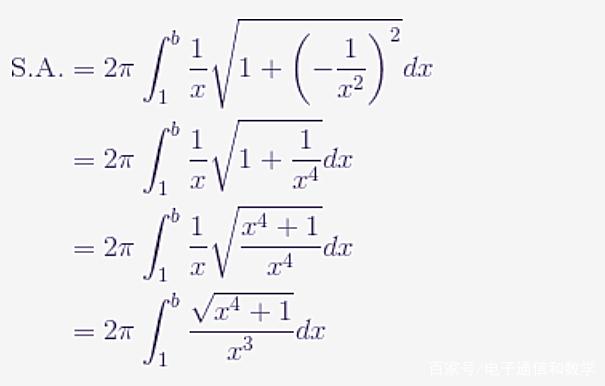
如果我们考虑分数的值,当 $x$ 变得非常大时,我们可以看到它会非常接近 $1/x$(但会比它大一点)
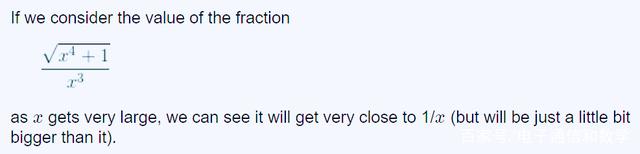
因此我们可以得出以下结论:
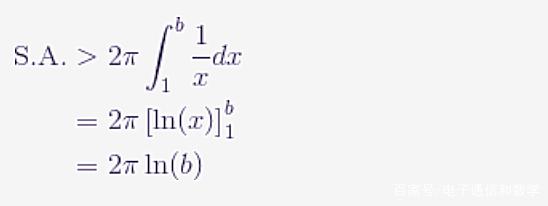
现在,随着 $b$ 越来越大,这个数量也越来越大。即,它是无限大的数量。
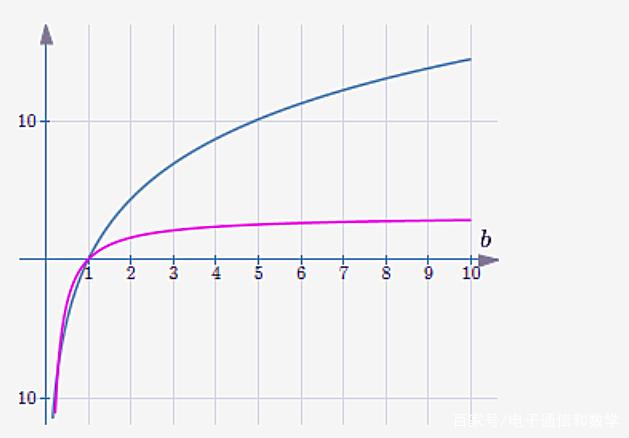
这是我们的两个解决方案的图,粉红色是体积 $V=π(1-1/b)$,绿色是表面积 $SA=2πln(b)$。我们可以看到体积趋向于极限 $π$,而表面积却不断增大。
todo
好多物理定律其实完全是由思维实验推导出来的,难以置信仅仅是思考竟然就能得出物理世界遵从的各种法则。经典的物理思维实验有 Newton 大炮、Galileo 斜塔实验、Schrödinger 的猫猫、Maxwell 的妖怪等等。还有,Turing 机也是一个伟大的思维实验。
参考
- [1] http://www.matrix67.com/blog/archives/773
- [2] 维基百科 · 加百列的号角
- [3] https://baijiahao.baidu.com/s?id=1660502466103090640
参考资料快照
 .
.