机器学习笔记 -- 数学×微积分入门
前言
微积分是对无穷小量的研究。无穷小量,简单说就是大小无限趋向于 $0$ 的量。微积分是微分和积分的总称,‘无限细分’就是微分,‘无限求和’就是积分。
微分主要研究两个无穷小量的比值 , 而积分学主要研究无限多的无穷小量之和 。
符号定义: \(d+\text{var}\) 表示某个变量的极小的一点变化。
$d$ 和 $\int$ 是可以互相抵消的,因为求导和求积分互为逆运算,这就好比平方和平方根可以抵消一样。
微分学中的符号“\(\textrm{d}x\)”、“\(\textrm{d}y\)”等,是由莱布尼茨首先使用。其中的 \(\textrm {d}\) 源自拉丁语中“差”(Differentia)的第一个字母。积分符号“\(\int _{}\,\)”亦由莱布尼茨所创,它是拉丁语“总和”(Summa)的第一个字母 \(s\) 的伸长(和 \(Σ\) 有相同的意义)。
导数
导数形式
对于任意函数 \(f(x)\),它的导数 \(f'(x)\) 为 \(\frac{df(x)}{dx}=\frac{f(x+dx)-f(x)}{dx}\)
导数定义
导数在数学上的含义是:经过图像上某一点的切线。
代数求导
考虑对 \(f(x)=x^3\) 求导数。
\[\begin{aligned} f'(x)&=\frac{df(x)}{dx} \\ &=\frac{f(x+dx)-f(x)}{dx} \\ &=\frac{(x+dx)^3-x^3}{dx} \\ &=\frac{x^3+3x^2(dx)+3x(dx^{2})+dx^3-x^3}{dx} \\ &=\frac{3x^2(dx)+3x(dx^{2})+dx^3}{dx} \\ &=3x^2+3x(dx)+dx^2 \end{aligned}\]当 \(dx\) 逼近 \(0\) 时,含 \(dx\) 的项可以忽略,所以最终 \(f'(x)=3x^2\)
几何求导
我们可以把 \(f(x)=x^2\) 看作求一个边长为 \(x\) 的正方形的面积,那么假设正方形的边长增加了一个 \(dx\),面积的增加量应该为 \(2x(dx)+dx^2\),写成导数形式即为 \(\frac{df}{dx}=2x+dx=2x\)
幂函数求导
对于任意幂函数 \(f(x)=x^n\),有 \(f'(x)=nx^{n-1}\)
组合函数求导
函数相加
\[\frac{d}{dx}(g(x)+h(x))=\frac{dg}{dx}+\frac{dh}{dx}\]函数乘积
\[f(x)=g(x)h(x)\] \[f'(x)=g(x)h'(x)+h(x)g'(x)\]复合函数
\[\frac{d}{dx}g(h(x))=\frac{dg}{dh}(h(x))\frac{dh}{dx}(x)\]指数函数求导
我们来看一个常见的指数函数 \(f(x)=2^x\)
\[f'(x)=2^x\frac{2^{dx}-1}{dx}\]当 \(dx\) 无限逼近于 \(0\) 时,可以得到后面这一项约等于 \(0.6931……\)
隐函数
极限
导数的正式定义
我们一般考虑导数时的操作是:选一个极小量 \(dx\),然后计算 \(\frac{df}{dx}\)
实际上,当 \(dx\) 无限逼近 \(0\) 时它才是真正的导数
写作 \(\frac{df}{dx}=\lim\limits_{h→0}\frac{f(x+h)-f(x)}{h}\)
极限的 ε-δ 定义
洛必达法则
\[\lim\limits_{x→a}f(a)=\frac{\frac{dg}{dx}(a)}{\frac{dh}{dx}(a)}\]如果 \(g(a)=0\),\(h(a)=0\),那么 \(\lim\limits_{x→a}\frac{g(x)}{h(x)}=\lim\limits_{x→a}\frac{g'(x)}{h'(x)}\)
\(ps\):洛必达法则是洛必达向伯努利买来的。
积分
积分
微积分基本定理
\[\int_{x}^{y}f(x)dx=F(x)-F(y)\]泰勒级数
泰勒级数
泰勒展开,本质上就是为了在某个点附近,用多项式函数取近似其他函数。泰勒公式,核心在逼近。拉格朗日余项,在于评估偏差。
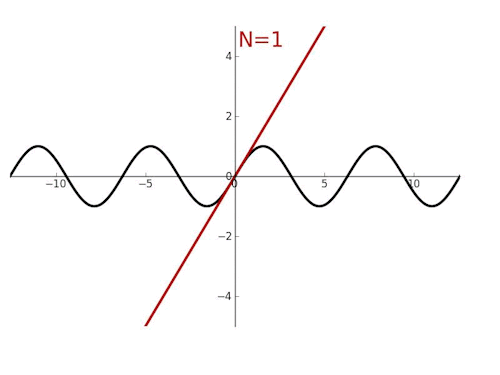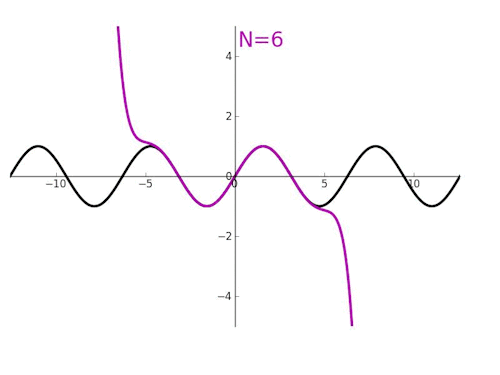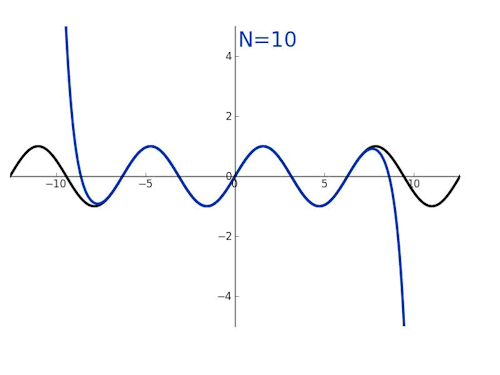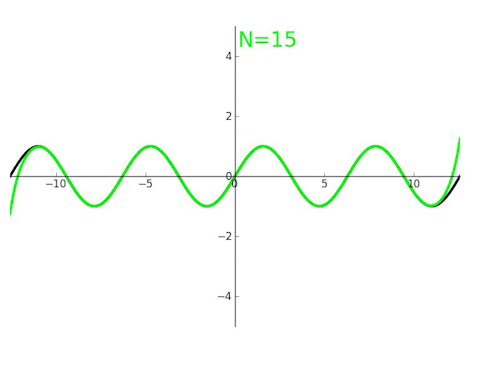
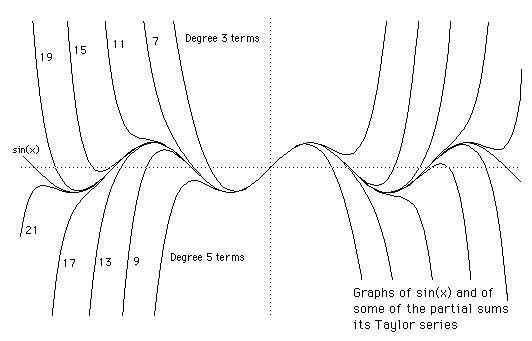
泰勒展开式的推导过程,视频:
https://haokan.baidu.com/v?pd=wisenatural&vid=8400832456233984742
参考
- [1] 《动手学深度学习》

- [2] 微积分入门
- [3] Html 转 MarkDown
- [4] 线性代数入门
- [5] 微积分到底是什么
- [6] 马同学 https://www.matongxue.com/madocs/247/
参考资料快照
- https://www.bilibili.com/video/BV1mb411r7bd
- https://haokan.baidu.com/v?pd=wisenatural&vid=8400832456233984742
- http://zh.gluon.ai/
- https://www.cnblogs.com/knife-rose/p/12120373.html
- http://www.fly63.com/tool/htmarkdown/
- https://www.cnblogs.com/knife-rose/p/12107204.html
- https://www.zhihu.com/question/336322284
- https://www.matongxue.com/madocs/247/
 .
.